그래프 (Graph)

그래프에 대한 공부를 이어서 하였다.

LeetCode 77.Combinations

전체 수 n을 입력받아 k개의 조합을 리턴하라.

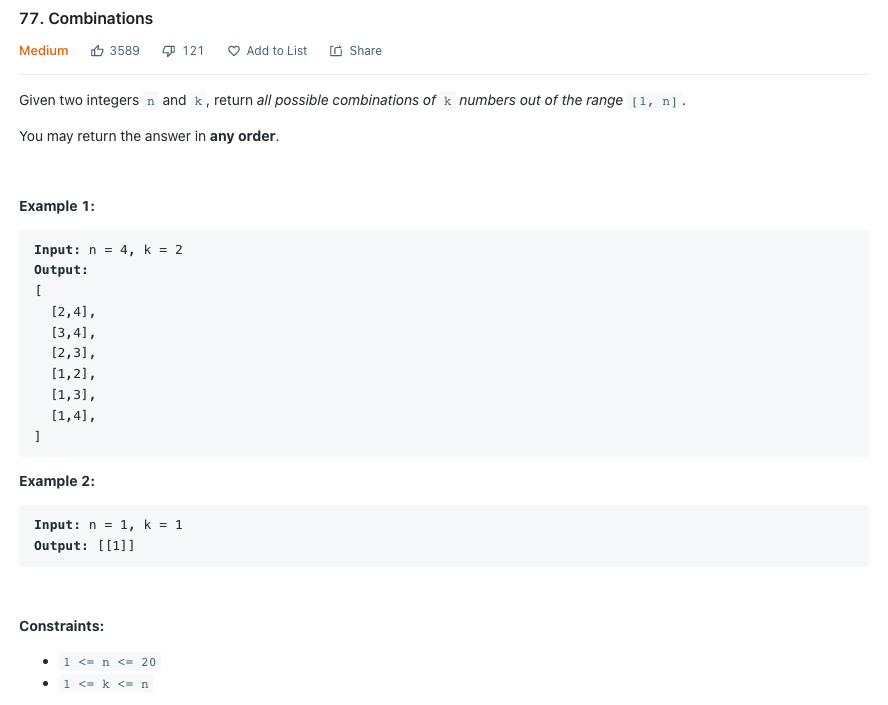
우선 혼자서 itertools를 이용하여 풀어보았다.

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        return list(itertools.combinations(range(1, n+1), k))

Solution 1 DFS로 k개 조합 생성

조합의 수를 구하는 수식은 n!/(k!(n-k)!)이다. 이 문제의 예시를 적용하면 6개의 결과값이 나와야 한다. 이렇게 개수를 구하는 문제는 쉽게 풀이가 가능하지만 모든 결과를 출력해야 하는 것은 다소 까다롭다.

순열의 경우 자기 자신을 제외하고 모든 요소를 next_elements로 처리하였고, 이와 달리 조합의 경우에는 자기 자신 뿐만 아니라 앞의 모든 요소를 배제하고 next_elements를 구성한다. 쉽게 말하면 next_elements는 자신보다 큰 수(뒤에 있는 수)가 된다. dfs 함수는 다음과 같이 작성할 수 있다.

def dfs(elements, start:int, k:int):
    if k==0:
        results.append(elements[:])
        return
    for i in range(start, n+1):
        elements.append(i)
        dfs(elements, i+1, k-1)
        elements.pop()

1부터 순서대로 for문으로 반복하되, 재귀 호출할 때 넘겨주는 값은 자기 자신 이전의 모든 값을 고정하여 넘긴다. 따라서 남아 있는 값끼리 나머지 조합을 수행하게 되며, k=0이 되면 결과에 삽입한다. elements를 results에 삽입할 때에는 참조로 처리되지 않도록 [:]를 사용하여 삽입해주었다. 전체 코드는 다음과 같다.

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        results=[]
        def dfs(elements, start:int, k:int):
            if k==0:
                results.append(elements[:])
                return
            for i in range(start, n+1):
                elements.append(i)
                dfs(elements, i+1, k-1)
                elements.pop()
        dfs([], 1, k)
        return results

Solution 2 itertools 모듈 사용

itertools모듈을 사용하면 한줄에 코드를 해결할 수 있다.

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        return list(itertools.combinations(range(1, n+1), k))

혼자서 풀었던 코드와 완벽하게 같았다. 확실히 itertools 모듈로 구현을 하면 처리 속도가 줄어드는 것을 볼 수 있었다.

순열과 조합

경우의 수를 구할 때, 모든 경우의 수를 하나씩 세는 것 보다는 공식을 이용하면 더 빠르게 계산할 수 있다. 순열과 조합이 식으로 경우의 수를 계산할 수 있는 예 중 하나이다. A, B, C, D, E 5장의 카드에서 3장의 카드를 골라 나열하여 세자리로 된 문자를 만드는 경우의 수는 몇가지인지 구하면 다음과 같다.

첫번째 카드에는 5장의 카드를 모두 사용할 수 있으므로 5가 되고, 두번째 카드에는 첫번째에 들어간 카드를 제외한 4가 된다. 세번째는 첫번째와 두번째를 제외한 3이 된다. 결과적으로 이 문제에서의 순열은 5x4x3=60이 된다.
n!/(n-r)! 식을 사용하여 구할 수 있는 셈이 된다.

조합은 순열과 조금 다르다. 조합의 경우에는 순열과 달리 순서에 상관하지 않는 경우의 수이다. ABC, BCA, CAB, ... 와 같이 ABC로 이루어진 어떤 경우도 같은 경우로 처리하기 된다. 따라서 조합의 개수는 순열의 전체 개수에서 동일한 카드로 볼 수 있는 경우의 수인 r!를 나눈 (n!/(n-r)!)/r!가 된다. 식을 정리하면 n!/(r!x(n-r)!)이 된다.

순열과 조합에 관련된 문제가 나올 경우에 브루트포스로 계산하는 것 보다 이렇게 식을 사용하게 되면 훨씬 유리하게 코딩이 가능하므로 잘 숙지하는 것이 좋다.

LeetCode 39.Combination Sum

숫자 집합을 조합하여 합이 target이 되는 원소를 나열하라. 각 원소는 중복으로 나열 가능하다.

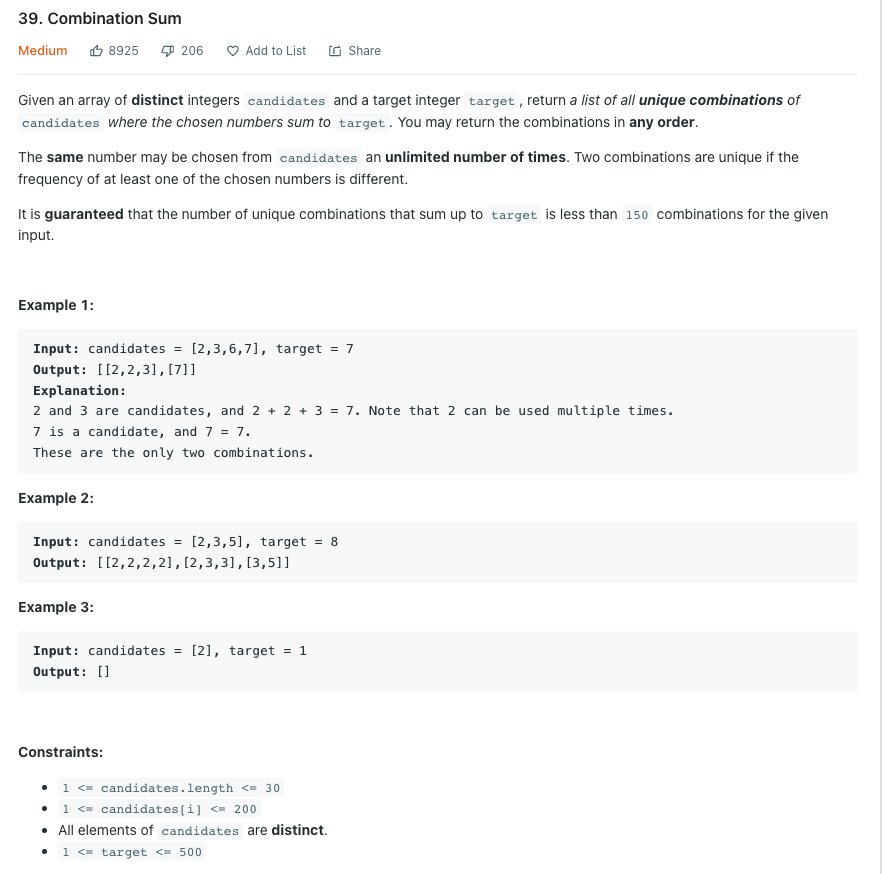
Solution 1 DFS로 중복 조합 그래프 탐색

앞서 순열과 조합 문제를 풀어보았다. 이번 문제는 조합을 응용한 문지로 합target을 만들 수 있는 모든 번호 조합을 찾는 문제인데 앞선 순열 문제와 유사하기 DFS로 풀이할 수 있다. [2, 3, 6, 7]이라는 리스트가 주어졌을 때 2는 2를 포함한 뒤에 있는 모든 수를 경우마다 고려할 수 있고, 3은 3을 포함한 뒤에 있는 모든 수를 경우마다 고려할 수 있다. 이 문제가 순열이었다면 자식 노드는 항상 처음부터 시작해야 하지만, 조합이기 때문에 자기 자신부터 뒤의 수들을 탐색하면 된다.

DFS로 재귀호출을 하되 dfs()함수의 첫번째 파라미터는 합을 갱신해나갈 csum, 두번째 파라미터는 순서, 세번째 파라미터는 지금까지의 탐색 경로로 지정한다. 이 탐색은 자기 자신을 포함하기 때문에 무한히 탐색하게 된다. 따라서 종료 조건이 필요하다. 종료 조건은 다음과 같다.

• csum<0: 목표값을 초과한 경우로 탐색을 종료
• csum=0: csum의 초기값은 target이므로 csum의 0은 target과 일치한다는 의미이므로 결과 리스트에 추가하고 탐색을 종료한다.

이러한 조건으로 인해 가지치기가 되어 더 이상 불필요한 탐색은 하지 않을 것이다. 전체 코드는 다음과 같다.

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        results=[]
        def dfs(csum, index, path):
            if csum<0:
                return
            if csum==0:
                results.append(path)
                return
            for i in range(index, len(candidates)):
                dfs(csum-candidates[i], i, path+[candidates[i]])
        dfs(target, 0, [])
        return results

LeetCode 78.Subsets

모든 부분 집합을 리턴하라.

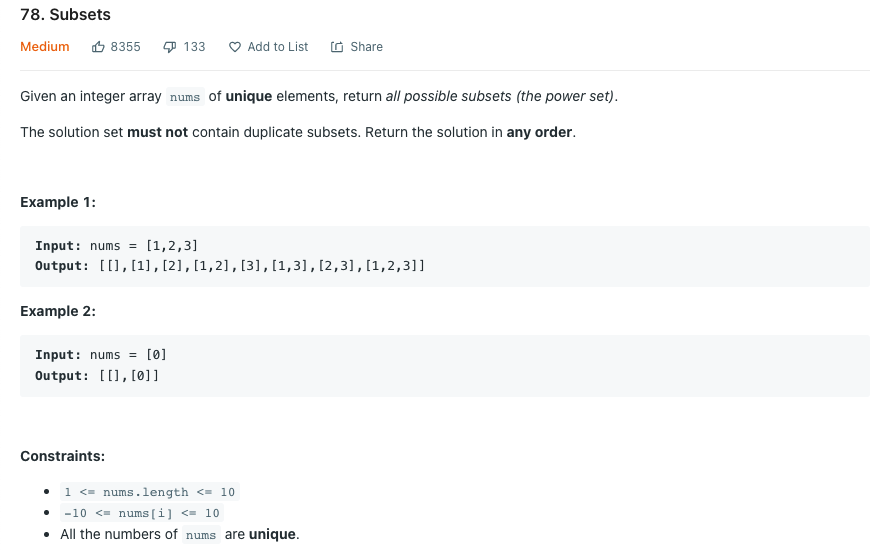
우선 혼자 문제를 풀어보았다. DFS를 이용하여 해결하였다.

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        results=[[]]
        def dfs(idx, subsets):
            if subsets not in results:
                results.append(subsets)
            for i in range(idx, len(nums)):
                dfs(i+1, subsets+[nums[i]])
        for i in range(len(nums)):
            dfs(i, [])
        return results

Solution 1 트리의 모든 DFS 결과

이 문제는 트리를 구성하고 트리를 DFS하는 문제로 풀이할 수 있다. 입력값이 [1, 2, 3]일 경우, 간단한 트리를 구성한다면 이를 DFS하여 원하는 결과를 출력할 수 있다.

def dfs(index, path):
    ...
    for i in range(index, len(nums)):
    	dfs(i+1, path+[nums[i]])

경로 path를 만들어 나가면서 인덱스를 1씩 증가하는 형태로 깊이 탐색한다. 별도의 종료 조건 없이 탐색이 끝나면 저절로 함수가 종료되게 한다. 그렇다면 결과는 언제 만들게 될까? 곰곰이 생각해보면 부분 집합은 모든 탐색의 경로가 결국 정답이 되므로 다음과 같이 탐색할 때마다 매번 결과를 추가하면 된다.

def dfs(index, path):
    ...
    result.append(path)

전체 코드는 다음과 같다.

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        results=[]
        def dfs(index, path):
            results.append(path)
            for i in range(index, len(nums)):
                dfs(i+1, path+[nums[i]])
        dfs(0, [])
        return results

내가 작성한 코드와 비슷하지만 훨씬 단순하게 코드가 작성되었다.

LeetCode 332.Reconstruct Itinerary

[from, to]로 구성된 항공권 목록을 이용해 JFK에서 출발하는 여행 일정을 구성하라. 여러 일정이 있는 경우 사전 어휘 순으로 방문한다.

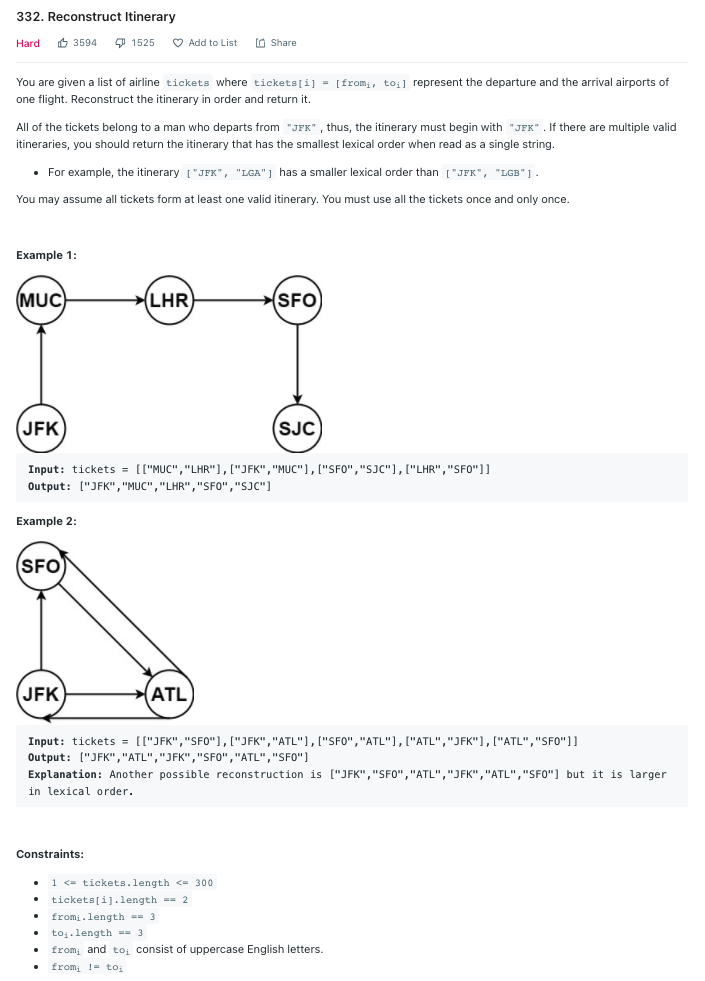
우선 혼자서 풀어보았다. 인접 리스트 방식으로 티켓 정보를 다시 저장하고 깊이 우선으로 순회하는 방식으로 접근하였다.

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        results=[]
        graph=collections.defaultdict(list)
        for f, t in sorted(tickets):
            graph[f].append(t)
        def dfs(cur):
            results.append(cur)
            if not graph[cur]:
                return
            for next in graph[cur]:
                dfs(next)
        dfs('JFK')
        return results

예제는 잘 돌아갔지만 큰 입력이 들어가면 재귀 에러가 발생하였다.

Solution 1 DFS로 일정 그래프 구성

티켓을 그래프로 구성하기 위해서는 다음과 같은 작업이 필요하다.

graph = collections.defaultdict(list)
for a, b in tickets:
    graph[a].append(b)
for a in graph:
    graph[a].sort()

인접 리스트 방식으로 딕셔너리에 각각 출발지에서 갈 수 있는 도착지를 저장하고, 사전 순으로 접근해야 하기 때문에 graph를 하나하나 오름차순으로 정렬해준다. 그러나 여기서 매번 sort()를 하는 것은 좋아보이지 않는다. 이를 파이썬의 sorted()함수로 한번만 정렬하는 형태로 변환할 수 있다.

graph = collections.defaultdict(list)
for a, b in sorted(tickets):
    graph[a].append(b)

이제 그래프에서 하나씩 꺼낼 차례이다. pop()으로 재귀 호출하면서 모두 꺼내 결과에 추가한다. 결과 리스트에는 역순으로 담기게 될 것이다. 그리고 pop()으로 처리했기 때문에 그래프에서 해당 경로는 사라지게 되어 재방문하게 되지 않는다.

def dfs(a):
    while graph[a]:
        dfs(graph[a].pop(0))
    route.append(a)

이 문제에서는 어휘순으로 방문해야 하기 때문에 pop(0)을 통해서 가장 앞에서부터 읽어야 한다. 전체 코드는 다음과 같다.

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        graph=collections.defaultdict(list)
        for a, b in sorted(tickets):
            graph[a].append(b)
        route=[]
        def dfs(a):
            while graph[a]:
                dfs(graph[a].pop(0))
            route.append(a)
        dfs('JFK')
        return route[::-1]

Solution 2 스택 연산으로 큐 연산 최적화 시도

Solution 1에서 큐의 연산(pop(0))을 수행하였다. 파이썬 리스트의 경우 파라미터를 지정하지 않은 값, 즉 pop()은 O(1)이지만 첫번째 값을 꺼내는 pop(0)은 O(n)이다. 따라서 더 효율적인 구현을 위해서는 pop()으로, 즉 스택 연산으로 처리할 수 있도록 개선해야 한다.

for a, b in sorted(ticktes, reverse='True):
    graph[a].append(b)
...
def dfs(a):
    while graph[a]:
        dfs(graph[a].pop())
    ...

이처럼 처음에 그래프를 역순으로 구성하게 되면 추출할 때에 pop()으로 처리가 가능하다. 그러나 실제로 리트코드에서는 성능의 차이가 크게 나지 않는다. 아마도 애초에 전체 딕셔너리가 아닌 각 키별 리스트의 입력값이 그리 크지 않기 때문으로 추정된다. 그러나 리스트가 매우 클 경우 pop()과 pop(0)의 차이는 클 수 있기 때문에 주의가 필요하다. 전체 코드는 다음과 같다.

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        graph=collections.defaultdict(list)
        for a, b in sorted(tickets, reverse=True):
            graph[a].append(b)
        route=[]
        def dfs(a):
            while graph[a]:
                dfs(graph[a].pop())
            route.append(a)
        dfs('JFK')
        return route[::-1]

Solution 3 일정 그래프 반복

이번 방법은 재귀가 아닌 반복으로 접근한다. 대부분의 재귀 문제는 반복으로 치환이 가능하며, 스택으로 풀이가 가능하다. 그래프를 구성하는 방식은 전과 같이 인접 리스트로 나타낸다.

graph = collections.defaultdict(list)
for a, b in sorted(tickets):
    graph[a].append(b)

이처럼 동일한 형태로 그래프를 구성하고, 끄집어낼 때 재귀가 아닌 스택을 이용한 반복으로 처리한다. 예제로 예를 들면 다음과 같다.

JFK: [ATL, SFO]
ATL: [JFK, SFO]
SFO: [ATL]
JFK->ATL->JFK->SFO->ATL->SFO

출발지는 항상 JFK이므로 가장 먼저 JFK가 오게 되고, 다음으로는 ATL이 어휘순으로 먼저 방문한다. ATL에서 어휘순 첫번째는 JFK이므로 JFK가 오게 되고, 다시 JFK로 돌아가면 전에 방문한 ATL의 다음 방문지인 SFO를 가게 된다.

한번 방문한 곳을 다시 방문하지 않으려면 별도로 마킹을 하여 다음번에는 방문하지 않도록 하거나, pop()으로 값을 제거해야 한다. 여기서는 스택을 사용하므로 pop()을 통해 값을 제거한다.

stack=['JFK']
    while graph[stack[-1]]:
    	stack.append(graph[stack[-1]].pop(0))

그래프에 값이 있다면 pop(0)으로 맨 처음의 값을 추출하여 스택 변수 stack에 넣게 하였다. 이는 큐의 연산이다. 이렇게 하면 그래프의 값들은 점점 제거될 것이고 마지막 방문지가 남지 않을때까지 while문을 계속 돌면서 위와 같은 순서로 처리가 된다.

이 예제는 경로가 끊어지는 경우가 없기 때문에 스택에 모든 경로가 한번에 담긴다. 그러나 만약 경로가 끊어지는 경우가 있다면 스택에 모든 경로가 한번에 담길 수 없다. 따라서 스택의 값을 다시 pop()하여 거꾸로 풀어낼 수 있는 또 다른 변수가 필요하다.

route, stack = [], ['JFK']
while stack:
    while graph[stack[-1]]:
    	stack.append(graph[stack[-1]].pop(0))
    route.append(stack.pop()

DFS 재귀 풀이와 달리 반복으로 풀이하면 이처럼 한번 더 풀어낼 수 있는 변수가 필요하다. 여기서는 최종 결과가 되는 변수이므로 DFS 재귀 풀이와 동일한 route로 변수명을 지정하였다. 여기에 스택을 pop()하여 담게 했다. 즉 경로가 풀리면서 거꾸로 담기게 된다. 따라서 마찬가지로 최종 결과는 다시 뒤집어서 반환해야 한다.

앞서 막혔던 부분을 결과변수 route에 pop()하여 막힌 부분부터 담게 되고 막히기 바로 전에서 다시 탐색을 시도해 다른 곳을 탐색하게 된다. 최종 결과는 다시 뒤집어서 반환된다. 전체 코드는 다음과 같다.

class Solution:
    def findItinerary(self, tickets: List[List[str]]) -> List[str]:
        graph=collections.defaultdict(list)
        for a, b in sorted(tickets):
            graph[a].append(b)
        route, stack=[], ['JFK']
        while stack:
            while graph[stack[-1]]:
                stack.append(graph[stack[-1]].pop(0))
            route.append(stack.pop())
        return route[::-1]

이 문제의 경우 재귀, 스택 연산, 반복 모두 속도 차이가 거의 없다. 재귀는 더 깔끔한 풀이가 가능하고 반복은 의식의 흐름대로 자연스럽게 풀이가 가능하다. 어느 쪽이든 더 선호하는 방법을 사용하면 된다.

그러나 면접관이 재귀나 반복 중 특정 방식을 요구할 수 있기 때문에 두 방법 모두 자유롭게 풀이할 수 있을 때까지 꾸준한 연습을 하는 것이 좋다.

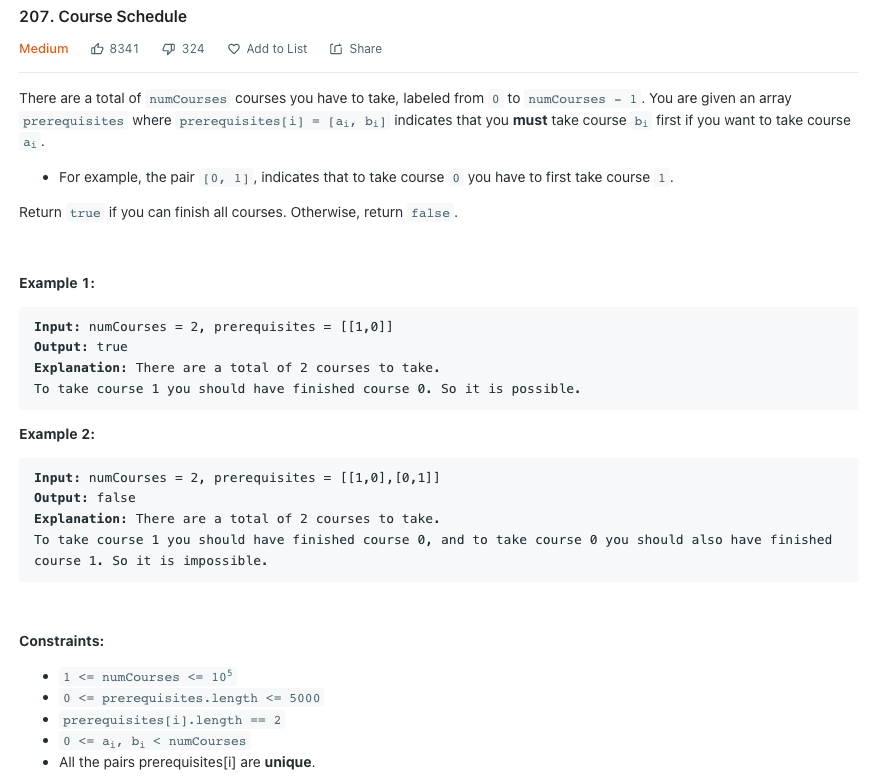
LeetCode 207.Course Schedule

0을 완료하기 위해서는 1을 끝내야 한다는 것을 [0, 1] 쌍으로 표현하는 n개의 코스가 있다. 코스 개수 n과 이 쌍들을 입력으로 받았을 때 모든 코스가 완료 가능한지 판별하라.

Solution 1 DFS로 순환 구조 판별

이 문제는 그래프가 순환 구조인지 판별하는 문제로 풀이할 수 있다. 순환 구조라면 계속 뱅글뱅글 돌게 될 것이고 해당 코스는 처리할 수 없기 때문이다. 따라서 순환 판별 알고리즘을 차례대로 구현해볼 것이다.

graph = collections.defaultdict(list)
for x, y in prerequisites:
    graph[x].append(y)

먼저 prerequisites 변수를 풀어서 인접 리스트 형태의 그래프로 표현한다.

traced = set()
...
for x in graph:
    if not dfs(x):
        return False
return True

순환 구조를 판별하기 위해 앞서 이미 방문했던 노드를 traced변수에 저장한다. 이미 방문했던 곳을 중복 방문하게 된다면 순환 구조로 간주할 수 있고, 이 경우 False를 반환하고 종료한다. traced는 중복값을 갖지 않기 때문에 set() 집합 자료형으로 구현했다. 순환 구조를 찾기 위한 탐색은 다음과 같이 DFS로 진행된다.

def dfs(i):
    if i in traced:
        return False
    traced.add(i)
    for y in graph[i]:
        if not dfs(y):
            return False
    traced.remove(i)
    return True

여기서 DFS 함수인 dfs()에서는 현재 노드가 이미 방문했던 노드 집합인 traced에 존재한다면 순환 구조로 간주하고 False를 반환한다. False는 계속 상위로 반환되어 최종 결과도 False를 반환할 것이다. 탐색은 재귀로 진행하되, 해당 노드를 이용한 모든 탐색이 끝나게 된다면 traced.remove(i)로 방문했던 내역을 반드시 삭제해야 한다. 그렇지 않으면 형재 노드가 방문한 노드까지 남게 되어 자식 노드 입장에서는 순환이 아님에도 순환으로 인지할 수 있다. 이 부분을 주의해서 코드를 작성해야 한다. 전체 코드는 다음과 같다.

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        graph=collections.defaultdict(list)
        for x, y in prerequisites:
            graph[x].append(y)
        traced=set()
        def dfs(i):
            if i in traced:
                return False
            traced.add(i)
            for y in graph[i]:
                if not dfs(y):
                    return False
            traced.remove(i)
            return True
        for x in list(graph):
            if not dfs(x):
                return False
        return True

책에서는 940밀리초에 풀린다고 되어 있지만 제출한 결과 시간 초과가 발생하였다.

Solution 2 가지치기를 이용한 최적화

좀 더 효율적으로 풀이할 수 있는 방법으로 가지치기가 있다. 만약 순환이 아니더라도 복잡하게 서로 호출하는 구조로 그래프가 구성되어 있다면 불필요하게 동일한 그래프를 여러 번 탐색하게 될 수도 있다. 따라서 한번 방문한 그래프는 두번 이상 방문하지 않도록 무조건 True로 반환하는 구조로 개선하면 탐색 시간을 줄일 수 있다.

visited = set()
def dfs(i):
    if i in traced:
        return False
    if i in visited:
        return True
    ...
    return True

이처럼 한번 방문했던 노드를 저장하기 위한 visited라는 별도의 set() 집합 변수를 만들고 이미 방문했던 노드라면 더 이상 진행하지 않고 True를 반환한다.

여기서 visited는 모든 탐색이 끝난 후에 노드를 추가하는 형태로 구현한다. 만약 탐색 도중 순환 구조가 발견된다면 False를 반환하면서 visited 추가는 하지 않음은 물론이고, 모든 함수를 빠져나가며 종료하게 될 것이다. 이렇게 한번 방문한 노드는 더 이상 탐색하지 않는 형태, 즉 가지치기로 최적화한 풀이의 전체 코드는 다음과 같다.

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        graph=collections.defaultdict(list)
        for x, y in prerequisites:
            graph[x].append(y)
        traced=set()
        visited=set()
        def dfs(i):
            if i in traced:
                return False
            if i in visited:
                return True
            traced.add(i)
            for y in graph[i]:
                if not dfs(y):
                    return False
            traced.remove(i)
            visited.add(i)
            return True
        for x in list(graph):
            if not dfs(x):
                return False
        return True

이렇게 가지치기로 최적화된 풀이의 실행속도는 거의 10배 빠른 속도이다. 간단한 최적화로 매우 좋은 성능을 낼 수 있었다.

defaultdict 순회 문제

LeetCode 207 풀이 중 graph를 순회하는 과정에서 다음과 같은 부분이 있다.

for x in list(graph):
   ...

graph를 list로 감싼 것을 볼 수 있다. 만약 list로 감싸지 않은 상태에서 graph 딕셔너리를 순회할 경우 RuntimeError: dictionary changed size during iteration이라는 에러가 발생한다. 해석해보면 딕셔너리가 순회 중 변경되었다고 말하고 있다. 이 문제는 graph를 defaultdict()로 선언했기 때문에 발생한 문제이다. defaultdict()는 키가 없는 딕셔너리에 대해서 빈 값 조회시 널 오류가 발생하지 않도록 처리해준다. 그래서 graph를 순회하는 중에 기본값을 value로 갖는 새로운 키값을 조회하게 되고 새로운 키가 생겨 딕셔너리가 변경되었다고 하는 것이다.

그렇기 떄문에 graph를 순회하기 위해서는 list()로 묶어서 해결해야 한다. 즉 새로운 복사본을 만들라는 이야기이다. 새로운 복사본의 여부는 ID 조회로 확인할 수 있다.

>>> id(graph)
4511667296
>>> id(list(graph))
4511666816

따라서 for문에서 graph를 순회하기 위해서는 list(graph)를 순회해야 한다.