배열

이전 글에 이어서 배열 문제를 조금 더 공부해보았다.

LeetCode 42.Trapping Rain Water

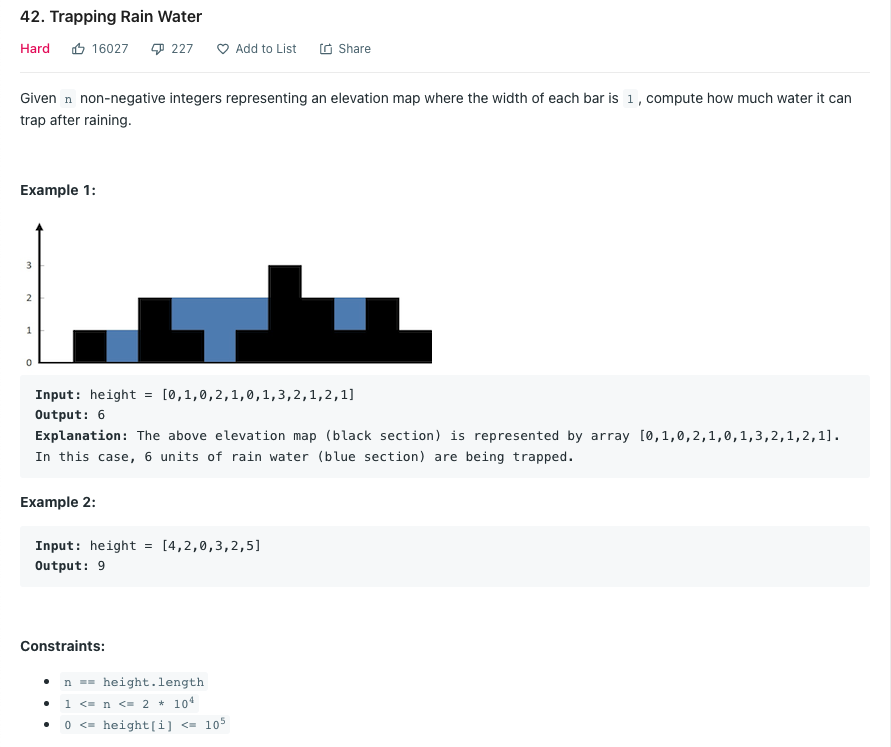
높이를 입력받아 비 온 후 얼마나 많은 물이 쌓일 수 있는지 계산하라.

Solution 1 투 포인터를 최대로 이동

이 문제는 높이와 너비를 모두 살펴보게 되면 O(n^2)라는 큰 시간이 소요된다. 그렇기 때문에 효율적인 코드를 찾아야 한다. 효율적인 방법 중 하나인 투 포인터로 먼저 접근해보았다.

문제에서 주어진 Example1의 그림을 보면 가장 높이가 높은 막대는 높이가 3이다. 막대는 높고 낮음과 무관하게 전체 부피에 영향을 끼치지 않으면서 왼쪽과 오른쪽을 가르는 장벽 역할을 하고 있다.

volume += left_max-height[left]
...
volume += right_max-height[right]

이처럼 최대 높이의 막대까지 각각 좌우 기둥 최대 높이 left_max, right_max가 현재 높이와의 차이만큼 물 높이 volume을 더해간다.

if left_max <= right_max:
    volume += left_max-height[left]
    left+=1
else:
    volume += right_max-height[right]
    right-=1

이 경우 적어도 낮은 쪽은 그만큼 항상 물이 채워진다. 두개의 포인터는 가운데로 점점 이동하게 된다. 오른쪽이 크다면 left+=1로 왼쪽이 이동하고 왼쪽이 크다면 right-=1로 오른쪽이 이동한다. 이렇게 하면 위의 그림에서 가장 높이가 높은 막대 지점에서 좌우 포인터가 서로 만나게 되어 O(n)에 풀이가 가능하다.

class Solution:
    def trap(self, height: List[int]) -> int:
        if not height:
            return 0
        volume=0
        left, right = 0, len(height)-1
        left_max, right_max = height[left], height[right]
        while left<right:
            left_max, right_max = max(height[left], left_max), max(height[right], right_max)
            if left_max <= right_max:
                volume += left_max-height[left]
                left+=1
            else:
                volume += right_max-height[right]
                right-=1
        return volume

62ms만에 해결된 것을 볼 수 있다.

Solution 2 스택 쌓기

이번에는 자료구조 스택을 이용한다. 현재 높이가 이전 높이보다 높을 때 격차만큼 물 높이를 채운다. 이전 높이는 고정된 형태가 아니라 들쑥날쑥하기 때문에 계속 스택으로 채워 나가다가 변곡점을 만날 때마다 스택에서 하나씩 꺼내면서 이전과의 차이만큼 물 높이를 채워 나간다. 스택으로 이전 항목들을 되돌아보면서 체크하기는 하지만 기본적으로 한번만 순회하기 때문에 O(n)으로 해결할 수 있다.

class Solution:
    def trap(self, height: List[int]) -> int:
        stack = []
        volume = 0
        for i in range(len(height)):
            while stack and height[i]>height[stack[-1]]:
                top = stack.pop()
                if not len(stack):
                    break
                distance = i - stack[-1] - 1
                waters = min(height[i], height[stack[-1]])-height[top]
                volume += distance*waters
            stack.append(i)
        return volume

72ms가 소요되었다.

정리

이 문제는 어려운 문제에 속한다. 원래의 나였다면 O(n)을 넘는 코드를 짰을 것 같다. 스택을 이용한 풀이는 직관적으로 떠올리기 어렵고 풀이 방법 또한 많이 고민해봐야 하기 때문에 코딩 테스트에서 마주하게 되었을 때 제대로 동작하는 코드를 작성하기 위해서는 적지 않은 시간이 필요할 것이다. 하지만 온사이트 인터뷰 시 면접관이 이 문제를 화이트보드에 풀어보라고 요구하는 경우에는 문제에서 주어진 그림을 그리는 정도로 개념을 잘 잡아서 설명하면 그리 어렵지 않게 해결할 수 있을 것이다. 투 포인터나 스택으로 개념을 잘 설명한다면 짧은 시간에 수도코드 풀이가 가능할 것이다.

LeetCode 15.3Sum

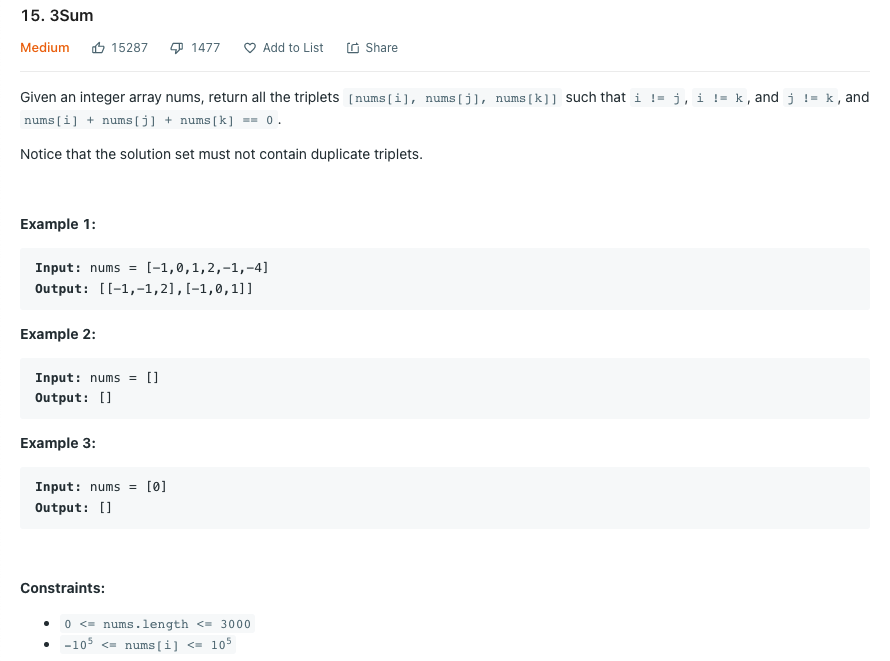
배열을 입력받아 합으로 0을 만들 수 있는 3개의 엘리먼트를 출력하라.

Solution 1 부르트 포스로 계산

우선 정말 간단하게 성능 체크 없이 접근한다면 브루트 포스 알고리즘으로 풀이가 가능하다. 다만 세 수의 합이기 때문에 O(n^3)이라는 매우 큰 시간 복잡도가 나올 것으로 예상된다.

우선 sort()함수로 배열을 오름차순 정렬해주고 i, j, k 포인터가 이동하면서 i+j+k=0의 경우를 찾게 된다. 중복된 값은 continue로 건너뛰도록 처리한다.

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        results=[]
        nums.sort()
        for i in range(len(nums)-2):
            if i > 0 and nums[i] == nums[i-1]:
                continue
            for j in range(i+1, len(nums)-1):
                if j > i+1 and nums[j] == nums[j-1]:
                    continue
                for k in range(j+1, len(nums)):
                    if k > j+1 and nums[k] == nums[k-1]:
                        continue
                    if nums[i]+nums[j]+nums[k]==0:
                        results.append([nums[i], nums[j], nums[k]])
        return results

당연하게도 시간 초과가 발생하였다.

Solution 2 투 포인터로 합 계산

시간 복잡도를 O(n^2)로 줄일 수 있는 방법이다. 우선 Solution 1과 같이 i를 축으로 하는 반복문은 그대로 사용한다. 이때 중복된 수를 거르는 if문도 그대로 사용한다. 만약 중복되지 않은 경우라면 i의 뒤에 있는 수들로 투 포인터 연산을 진행한다. left는 i+1, right는 len(nums)-1로 두고 left와 right의 합이 i가 되는 경우를 찾아 넣는 방식이다. 이때 sum이 0보다 작다면 수를 키워야 하므로 left를 증가시키고 0보다 크다면 수를 줄여야 하므로 right를 줄인다.

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        results=[]
        nums.sort()
        for i in range(len(nums)-2):
            if i > 0 and nums[i] == nums[i-1]:
                continue
            left, right = i+1, len(nums)-1
            while left<right:
                sum = nums[i]+nums[left]+nums[right]
                if sum < 0:
                    left+=1
                elif sum > 0:
                    right-=1
                else:
                    results.append([nums[i], nums[left], nums[right]])
                    while left<right and nums[left] == nums[left+1]:
                        left+=1
                    while left<right and nums[right] == nums[right-1]:
                        right-=1
                    left+=1
                    right-=1            
        return results

906ms 안에 돌아가는 것을 볼 수 있다.

투 포인터

투 포인터란 여러 가지 방식이 있지만 대개는 시작점과 끝점 또는 왼쪽 포인터와 오른쪽 포인터 두 지점을 기준으로 하는 문제 풀이 전략을 뜻한다. 범위를 좁혀 나가기 위해서는 일반적으로 배열이 정렬되어 있을 때 좀 더 유용하다. 세 수의 합 문제 또한 정렬된 배열을 이용하는 대표적인 투 포인터 풀이이다. 이 풀이로 O(n^3)을 O(n^2)로 개선할 수 있었다.

LeetCode 561.Array Partition 1

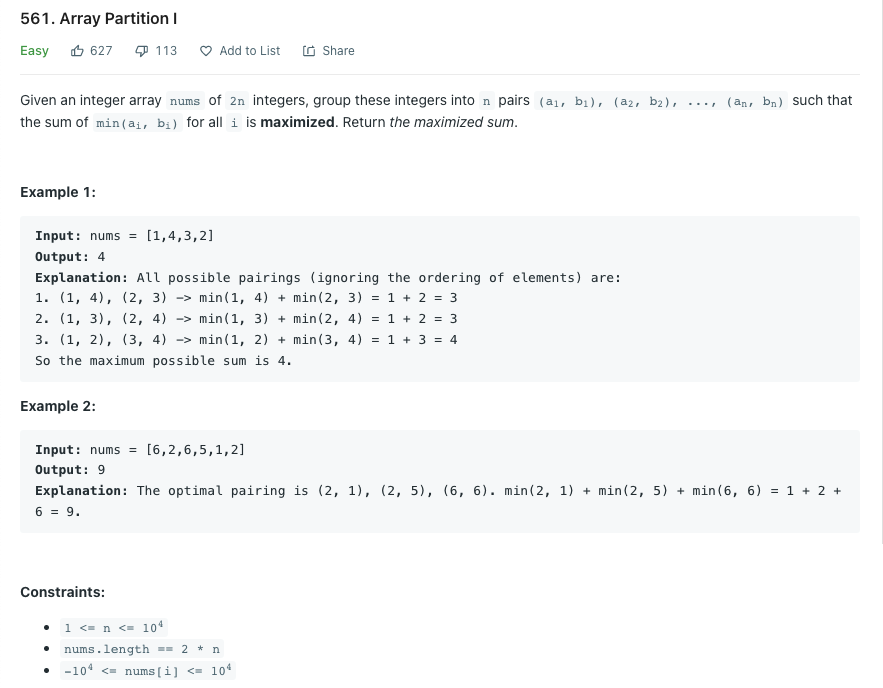
n개의 페어를 이용한 min(a, b)의 합으로 만들 수 있는 가장 큰 수를 출력하라.

Solution 1 오름차순 풀이

이 문제는 페어의 min()을 합산하였을 때에 가장 큰 수를 출력하는 문제이므로 페어의 min()이 되도록 커야 한다. 뒤에서부터 내림차순으로 집어넣으면 항상 최대 min() 페어를 유지할 수 있다. 2n개의 수가 들어가므로 앞에서부터 오름차순으로 넣어도 결과는 같을 것이다.

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        pair = []
        nums.sort()
        for n in nums:
            pair.append(n)
            if len(pair)==2:
                sum+=min(pair)
                pair=[]
        return sum

292ms의 시간이 걸렸다.

Solution 2 짝수 번째 값 계산

페어에서 min()값을 일일이 구하지 않아도 짝수 번째 값을 더하면 해결할 수 있을 것 같다. 정렬된 상태에서는 짝수 번째에 항상 작은 값이 위치하기 때문이다. 이는 불필요한 리스트 변수를 생략할 수 있기 때문에 코드 또한 많이 줄어들어 간결하게 코딩 가능하다.

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        sum = 0
        nums.sort()
        for i, n in enumerate(nums):
            if i%2==0:
                sum+=n
        return sum

Solution 3 파이썬다운 방식

이 코드를 파이썬다운 방식으로 작성하면 한줄로도 풀이가 가능하다. 슬라이싱을 이용했다.

class Solution:
    def arrayPairSum(self, nums: List[int]) -> int:
        return sum(sorted(nums)[::2])

이 풀이가 코드도 가장 짧고 슬라이싱을 사용한 덕분에 성능 또한 가장 좋다.

LeetCode 235.Product of Array Except Self

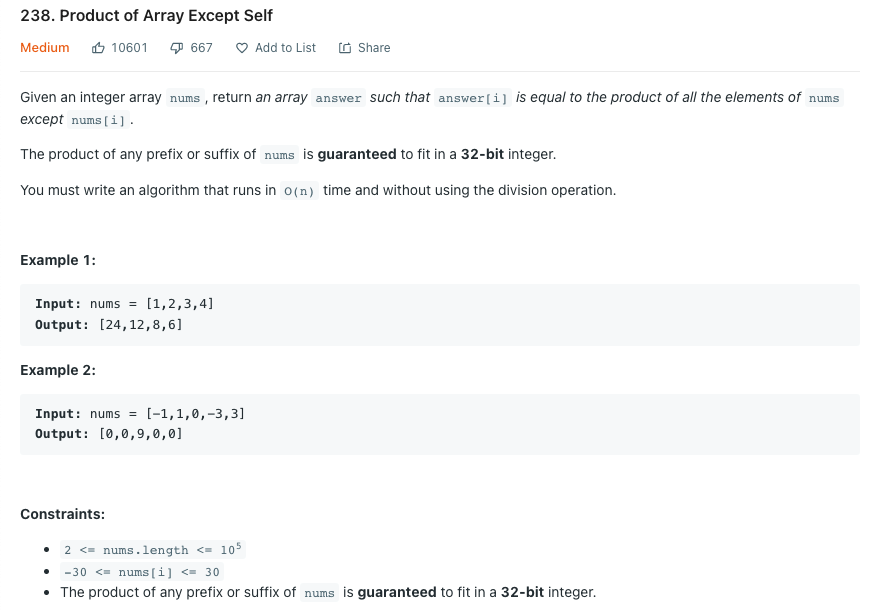
배열을 입력받아 output[i]가 자신을 제외한 나머지 모든 요소의 곱셈 결과가 되도록 출력하라.

Solution 1 왼쪽 곱셈 결과에 오른쪽 값을 차례대로 곱셈

이 문제에는 중요한 제약사항이 있는데 그것은 바로 '나눗셈을 하지 않고 O(n)에 풀이하라'는 점이다. 이 말은 당장 머리속에서 떠오르는 풀이법인 모든 수를 곱한 수에서 해당 수만 나누는 방식이 사용 불가하다는 얘기이다. 풀이방법은 자기 자신을 제외하고 왼쪽의 곱셈 결과와 오른쪽의 곱셈 결과를 곱해야한다.

왼쪽의 곱셈 결과는 out배열에 담기게 되고 out 변수를 재활용함으로써 O(n)을 O(1)로 개선한다.

p=1
for i in range(0, len(nums)):
    out.append(p)
    p=p*nums[i]

이 다음 왼쪽의 곱셈 결과에 오른쪽 마지막 값부터 차례대로 곱해 나간다.

class Solution:
    def productExceptSelf(self, nums: List[int]) -> List[int]:
        out = []
        p=1
        for i in range(0, len(nums)):
            out.append(p)
            p=p*nums[i]
        p=1
        for i in range(len(nums)-1, 0-1, -1):
            out[i]=out[i]*p
            p=p*nums[i]
        return out

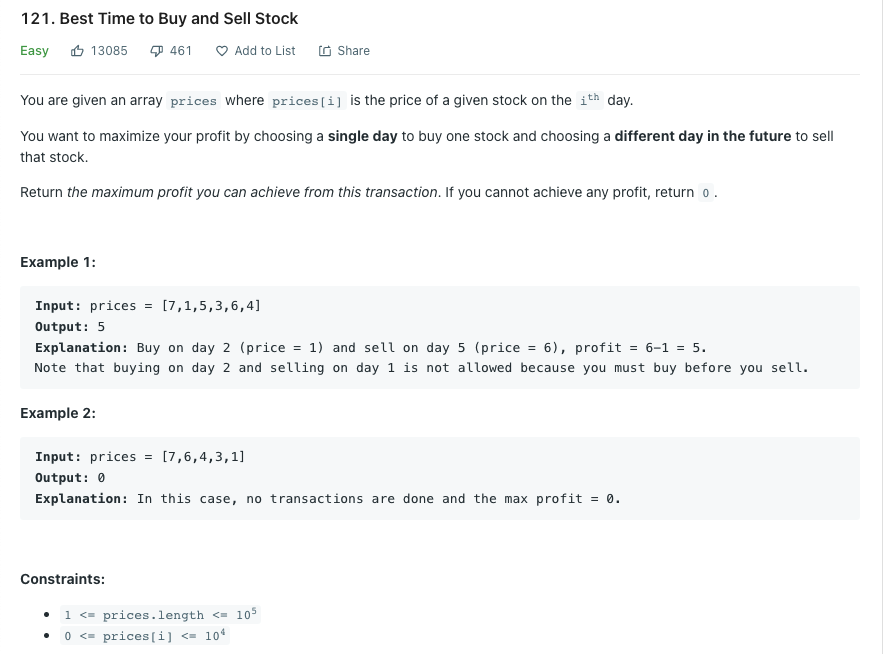
LeetCode 121.Best Time to Buy and Sell Stock

한 번의 거래로 낼 수 있는 최대 이익을 산출하라.

Solution 1 브루트 포스로 계산

이 문제는 저점에 사고 고점에 팔아서 낼 수 있는 최대 이익을 찾는 문제이다. 가장 먼저 간단한 브루트 포스로 접근해보았다.

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        max_price = 0
        for i, price in enumerate(prices):
            for j in range(i, len(prices)):
                max_price = max(prices[j]-price, max_price)
        return max_price

로직은 맞지만 예상대로 시간 초과가 발생하였다.

Solution 2 저점과 현재 값과의 차이 계산

입력값을 그래프로 그려 시각화하면 풀이법을 더 쉽게 찾을 수 있는 경우가 발생하기도 한다. 이와 같은 시각화는 기술 통계학이라고도 일컬으며 통계학에서도 매우 중요한 연구 분야 중 하나이다.

현재값을 가리키는 포인터가 우측으로 이동하면서 이전 상태의 저점을 기준으로 가격 차이를 계산하고 만약 클 경우 최대값을 계속 교체하는 방식으로 O(n)에 해결할 수 있다.

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        profit = 0
        min_price = sys.maxsize
        for price in prices:
            min_price = min(min_price, price)
            profit = max(profit, price - min_price)
        return profit

이는 카데인 알고리즘을 응용한 풀이이다. 카데인 알고리즘은 다음에 한번 알아볼 것이다.