연결 리스트

연결 리스트는 컴퓨터과학에서 배열과 함께 가장 기본이 되는 대표적인 선형 자료구조 중 하나이다. 추상 자료형 구현의 기반이 된다. 동적으로 새로운 노드를 삽입하거나 삭제하기가 간편하며 연결 구조를 통해 물리 메모리를 연속적으로 사용하지 않아도 되기 때문에 관리하기도 쉽다. 데이터 구조체로 묶어서 포인터로 연결하는 개념은 여러가지 방법으로 다양하게 활용이 가능하다. 실제로 컴퓨터의 물리 메모리에는 구조체 각각이 서로 연결된 형태로 구성되어 있으며 메모리 어딘가에 흩뿌려져 있는 형상을 띤다.

연결 리스트는 특정 인덱스로 접근할 때에 일반 배열처럼 주소값을 바로 찾아가는 방식이 아니기 때문에 O(n)의 시간 복잡도가 소요된다. 그러나 연결 리스트의 가장 앞이나 가장 뒤에 추가, 삭제, 추출할 때에는 O(1)에 가능하다.

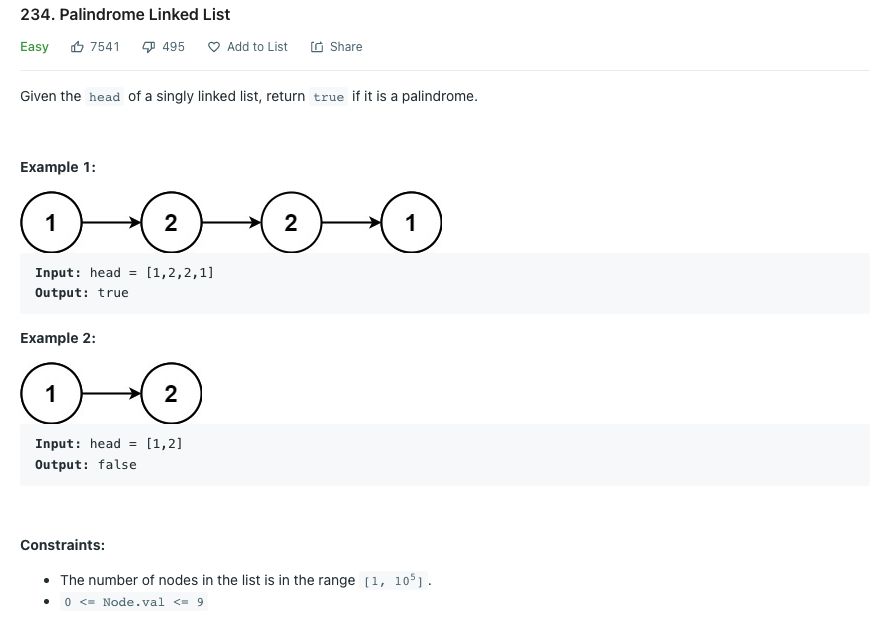
LeetCode 234.Palindrome Linked List

연결 리스트가 팰린드롬 구조인지 판별하라.

Solution 1 리스트 변환

팰린드롬 여부를 판별하기 위해서는 앞뒤로 모두 추출할 수 있는 자료구조가 필요하다. 일반적인 스택 자료구조는 마지막 요소만 추출하는 연산이 있지만 파이썬의 리스트는 pop()에 인덱스를 지정하여 처리할 수 있기 때문에 마지막 요소가 아니어도 얼마든지 원하는 위치를 자유롭게 추출할 수 있다. 따라서 이 문제는 연결 리스트를 파이썬의 리스트로 변환하여 리스트의 기능을 이용하여 쉽게 풀이할 수 있다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        q: List = []
        if not head:
            return True
        node = head
        while node is not None:
            q.append(node.val)
            node = node.next
        while len(q)>1:
            if q.pop(0) != q.pop():
                return False
        return True

이렇게 연결 리스트를 파이썬의 리스트로 변환하여 풀이하면 쉽게 풀 수 있다.

Solution 2 데크를 이용한 최적화

리스트로 이 문제를 해결할 경우 q.pop(0)이 부분에서 O(n)이라는 시간 복잡도가 발생한다. 그 이유는 배열의 빈 자리를 그 뒤의 원소들을 앞으로 땡겨옴으로써 채우기 때문이다. 이 부분을 데크를 이용하여 처리한다면 O(1)에 가능하게 된다.

데크(Deque)는 이중 연결 리스트 구조로 양쪽 방향 모두 추출하는데 시간 복잡도가 O(1)이다. 만약 리스트로 처리했을 때 타임아웃이 발생하거나 오프라인 코딩 인터뷰에서 면접관이 이 코드가 효율적인가?라는 질문을 했을 때 양방향 모두 O(1)에 가능한 데크를 설명한 후 이 자료형을 적용할 것이라는 점을 설명하면 좋을 것이다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        q: Deque = collections.deque()
        if not head:
            return True
        node = head
        while node is not None:
            q.append(node.val)
            node = node.next
        while len(q)>1:
            if q.popleft() != q.pop():
                return False
        return True

pop(0) 대신 popleft()를 사용하기만 했는데 성능이 매우 좋아진 것을 볼 수 있다. 이렇게 리스트의 시작점과 끝점을 모두 봐야 하는 경우에는 데크를 사용하면 효율적인 코드를 작성할 수 있다.

Solution 3 런너를 이용한 우아한 풀이

팰린드롬 연결 리스트 문제의 제대로 된 풀이법은 런너(Runner) 기법을 활용하는 것이다.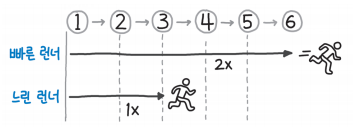
런너 기법은 위의 그림처럼 빠른 런너와 느린 런너를 각각 출발시키게 된다. 빠른 런너가 2배 빠르게 이동하게 되고 빠른 런너가 마지막에 도달하면 느린 런너는 딱 가운데에 위치하게 된다. 느린 런너는 중간까지 이동하면서 역순으로 연결 리스트 rev를 만들어 나가고 중간부터 나머지 경로로 이동할 때에 역순으로 만든 연결 리스트의 값들과의 일치를 확인해 나간다.

빠른 런너와 느린 런너 모두 head에서 시작한다.

slow = fast = head

런너의 이동은 next가 존재하지 않을 때까지 반복되며 빠른 런너는 두칸씩, 느린 런너는 한칸씩 이동한다.

while fast and fast.next:
    fast = fast.next.next
    ...
    slow = slow.next

빠른 런너가 두칸씩 이동하는 동안 느린 런너는 한칸씩 이동하며 역순 연결 리스트를 만든다.

while fast and fast.next:
    fast = fast.next.next
    rev, rev.next, slow = slow, rev, slow.next

빠른 런너가 도착하면 이제 팰린드롬 여부를 확인할 차례이다. 역순 연결 리스트 rev를 반복한다.

while rev and rev.val == slow.val:
    slow, rev = slow.next, rev.next

느린 런너의 나머지 이동 경로와 역순 연결 리스트 rev의 노드를 하나씩 풀어가며 비교한다. 정상적으로 종료되면 slow와 rev가 모두 None이 될 것이다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def isPalindrome(self, head: Optional[ListNode]) -> bool:
        rev = None
        slow = fast = head
        while fast and fast.next:
            fast = fast.next.next
            rev, rev.next, slow = slow, rev, slow.next
        if fast:
            slow = slow.next
        while rev and rev.val == slow.val:
            slow, rev = slow.next, rev.next
        return not rev

데크로 구현한 풀이와 성능은 비슷하지만 연결 리스트를 다른 자료형으로 변환하거나 편법을 사용하지 않고 그 자리에서 바로 풀이함으로써 좀 더 연결 리스트답게 우아한 방식으로 풀 수 있었다.

런너 기법

런너는 연결 리스트를 순회할 때에 2개의 포인터를 사용하는 기법이다. 한 포인터가 다른 포인터보다 앞서게 하여 병합 지점이나 중간 위치, 길이 등을 판별할 때에 유용하다. 2개의 포인터는 빠른 런너와 느린 런너로 나뉘고, 일반적으로 빠른 런너는 2칸씩, 느린 런너는 1칸씩 이동한다. 이때 빠른 런너가 마지막에 도달한 시점에 느린 런너는 정확히 중간에 위치하게 되고 이를 통하여 값을 비교하거나 뒤집기를 시도하는 등 여러모로 활용할 수 있기 때문에 연결 리스트에서 반드시 쓰이는 기법이다.

다중 할당

파이썬에서 다중 할당이란 2개 이상의 값을 2개 이상의 변수에 동시에 할당하는 것이다.

a, b = 1, 2

위의 코드는 간단한 다중 할당의 예이다. 이처럼 한번에 여러 개의 값을 여러 변수에 할당할 수 있는 파이썬의 독특한 다중 할당 문법은 매우 유용하며 여러모로 쓰임새가 많다. 앞서 풀이 또한 다중 할당을 이용해 효율적으로 풀이할 수 있었다.

rev, rev.next, slow = slow, rev, slow.next

다중 할당을 처음 본다면 가독성을 떨어트리는 라인을 왜 작성했을까 라는 의문이 들 수도 있다. 이 코드를 세줄로 정리하게 되면 다음과 같다

fast = fast.next.next
rev, rev.next = slow, rev
slow = slow.next

이 코드가 훨씬 가독성이 좋지만 아쉽게도 이렇게 작성할 경우 위의 문제가 해결되지 않는다. 그 이유는 구문 중간에 rev=slow가 있기 때문이다. 이는 서로 같은 값을 참조하게 되는 것이다. 파이썬은 모든 것이 객체이기 때문에 = 연산자를 이용해 할당을 진행하게 되면 값을 할당하는 것이 아니라 이 불변 객체에 대한 참조를 할당한다.

다중 할당을 할 경우 그 작업들이 동시에 일어나기 때문에 중간 과정 없이 한번에 트랜잭션으로 끝나게 된다. 그러나 두 줄 분기 코드의 경우에는 참조의 오류가 생겨 원하는 결과를 얻을 수 없다.

파이썬에서의 할당은 C++이나 자바와 개념이 조금 다르기 때문에 이런 부분에 대해서 잘 알고 주의해서 코드를 작성해야 한다.

LeetCode 21.Merge Two Sorted Lists

정렬되어 있는 두 연결 리스트를 합쳐라

Solution 1 재귀 구조로 연결

여기서는 정렬된 리스트라는 점이 중요하다. 즉 병합 정렬에서 마지막 조합 시 첫번째 값부터 차례대로만 비교하면 한 번에 해결되듯이 이 또한 병합 정렬의 마지막 조합과 동일한 방식으로 첫번째부터 비교하면서 리턴하면 쉽게 풀 수 있다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        if (not list1) or (list2 and list1.val > list2.val):
            list1, list2 = list2, list1
        if list1:
            list1.next = self.mergeTwoLists(list1.next, list2)
        return list1

풀이가 명확하고 코드도 짧다. 그러나 이 코드에는 많은 내용이 함축되어 있다. 또한 재귀가 포함되어 있어 이해하기가 어려울 수 있다.

이 코드를 다시 보면 list1과 list2를 비교하여 작은 값이 왼쪽에 오도록 하고, next는 그 다음 값이 엮이도록 재귀 호출을 하는 것이 이 코드의 전부이다. 이렇게 list1과 list2를 업데이트 하며 원하는 구조의 리스트가 만들어 질 때가지 반복한다.

재귀 함수의 경우 많이 접해보고 생각해보면서 익숙해지는 것이 가장 중요한 것 같다.

연산자 우선순위

연산자 우선 순위를 잘 기억해두면 코드를 짤 때 도움이 될 때가 많다. 가장 중요한 것은 우선 순위가 모호한 경우 괄호를 잘 활용하여 연산자의 순서를 잘 지정하는 것이다.

변수 스왑

두 변수를 스왑하는 가장 일반적이고 널리 사용되는 방법은 임시 변수를 사용하는 방법이다.

tmp = a
a = b
b = tmp

이 방법은 거의 모든 언어에서 사용가능하다. 그러나 파이썬은 다음과 같은 간단한 방식으로도 변수 스왑이 가능하다.

a, b = b, a

이는 위에서 보았던 다중 할당을 이용한 방법으로 파이썬에서 변수를 스왑하는 방법 중 가장 좋은 방법이다. 속도 역시 임시 변수를 이용하는 방법과 거의 비슷하다.
C++ 역시 STL을 통해 swap함수를 지원한다. 그러나 자바의 경우에는 임시 변수를 사용해서 구현해야 한다.

숫자형인 경우 덧셈 뺄셈을 통해 임시 변수 없이 스왑할 수 있는 방법이 있다.

x+=y
y = x-y
x -= y

x가 9이고 y가 4라고 가정한다면 x에 y를 더해 일단 13을 만들어준다. 그리고 y는 13-4를 해줌으로써 원래 x의 값이었던 9를 저장하고, x는 x에서 업데이트 된 y의 크기인 9를 빼줘서 4를 저장하게 된다. 간혹 면접관이 이런 질문을 하는 경우가 있는데 이런 수학 문제 유형의 질문에 대해 답을 찾아낼 수 있다면 똑똑한 이미지를 심어줄 수 있다.

LeetCode 206.Reverse Linked List

연결 리스트를 뒤집어라.

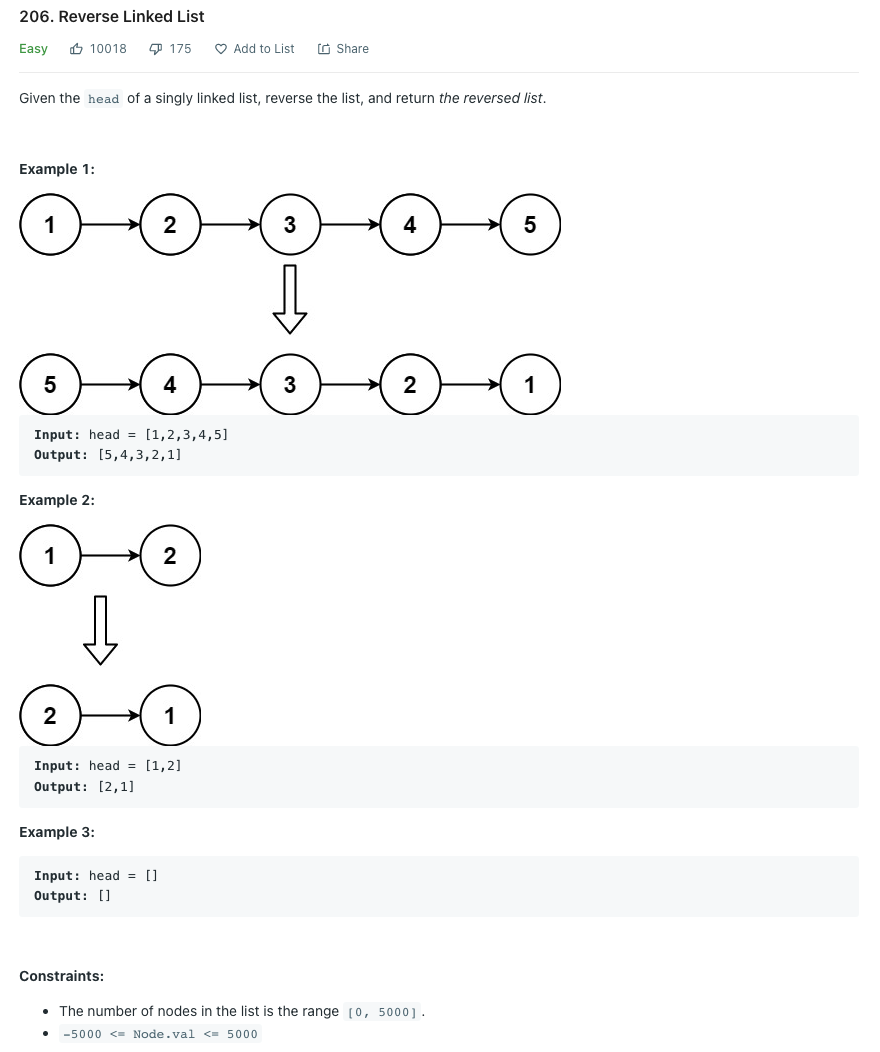
이번에는 답을 보기 전에 스스로 한번 풀어보았다. 다중 할당을 사용하여 O(n) 안에 해결되었다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        rev=None
        while head:
            rev, rev.next, head = head, rev, head.next
        return rev

Solution 1 재귀 구조로 뒤집기

연결 리스트를 뒤집는 문제는 매우 일반적이면서도 활용도가 높은 문제로 실무에서도 빈번하게 쓰인다. 재귀 구조와 반복 구조, 2가지 방식으로 모두 풀이가 가능하다. 먼저 재귀 풀이이다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        def reverse(node: ListNode, prev: ListNode = None):
            if not node:
                return prev
            next, node.next = node.next, prev
            return reverse(next, node)
        return reverse(head)

다음 노드 next와 현재 노드 node를 파라미터로 지정한 함수를 재귀 호출한다. node.next에는 이전 prev 리스트를 계속 연결해주고 node가 None이 될 때까지 재귀호출을 하면 마지막에는 백트래킹을 통해 연결 리스트가 거꾸로 연결된다. 여기서 맨 처음에 반환된 prev는 뒤집힌 연결 리스트의 첫번째 노드가 된다.

Solution 2 반복 구조로 뒤집기

node.next를 이전 prev 리스트로 계속 연결하면서 끝날 때까지 반복한다. node가 None이 될 때 prev는 뒤집힌 연결 리스트의 첫번째 노드가 된다. next, node.ext = node.next, prev로 다중 할당하는 부분은 재귀나 반복 모두 동일하다.

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        node, prev = head, None
        while node:
            next, node.next = node.next, prev
            prev, node = node, next
        return prev

정리

반복이 재귀에 비해 70% 수준의 메모리를 차지하여 공간 복잡도가 더 낮고, 실행속도 또한 조금 더 빠르다.

To be continue ...