비트 조작
비트 조작에 대해 이어서 알아보았다.
LeetCode 136.Single Number
딱 하나를 제외하고 모든 엘리먼트는 2개씩 있다. 1개인 엘리먼트를 찾아라.
Solution 1 XOR 풀이
단 1개의 엘리먼트를 찾는 적당한 연산자가 있다. 바로 XOR 연산이다. XOR은 입력값이 서로 다르면 True, 서로 동일하면 False를 반환한다. 이를 십진수에 적용하면 다음과 같은 결과를 확인할 수 있다.
>>> 0 ^ 0
0
>>> 4 ^ 0
4
>>> 4 ^ 4
0두 번 등장한 엘리먼트는 0으로 초기화되고 한 번만 등장하는 엘리먼트는 그 값을 온전히 보존한다. 즉 배열의 모든 값을 XOR 하면, 단 한 번 등장하는 엘리먼트만 그 값을 유지하게 된다. 전체 코드는 다음과 같다.
class Solution:
def singleNumber(self, nums: List[int]) -> int:
result=0
for num in nums:
result^=num
return result
LeetCode 461.Hamming Distance
두 정수를 입력받아 몇 비트가 다른지 계산하라.
우선 비트 연산자를 이용하여 혼자 풀어보았다. 다른 비트의 수를 도출하기 위해서는 XOR 연산을 적용한 문자열에서의 1의 갯수를 반환해야 한다.
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
result=x^y
return bin(result).count('1')
Solution 1 XOR 풀이
자연어 처리에서도 널리 쓰이는 해밍 거리는 두 정수 또는 두 문자열의 차이를 말한다. 역시 책에서도 XOR연산을 통해 이 문제를 해결하였다.
class Solution:
def hammingDistance(self, x: int, y: int) -> int:
return bin(x^y).count('1')
LeetCode 371.Sum of Two Integers
두 정수 a와 b의 합을 구하라. + 또는 - 연산자는 사용할 수 없다.
+, - 연산자를 사용하지 못한다는 점에서 비트 연산으로 해결해야 될 것 같다는 생각을 했지만 아직 미숙하기 때문에 파이썬의 내장 함수를 이용하여 풀어 보았다.
class Solution:
def getSum(self, a: int, b: int) -> int:
return sum([a, b])
Solution 1 전가산기 구현
두 정수의 합을 구하는 데 덧셈이나 뺄셈을 사용할 수 없기 때문에, 비트 연산만으로 풀이해야 하는 문제이다. 전가산기를 직접 구현하여 풀이해볼 것이다.
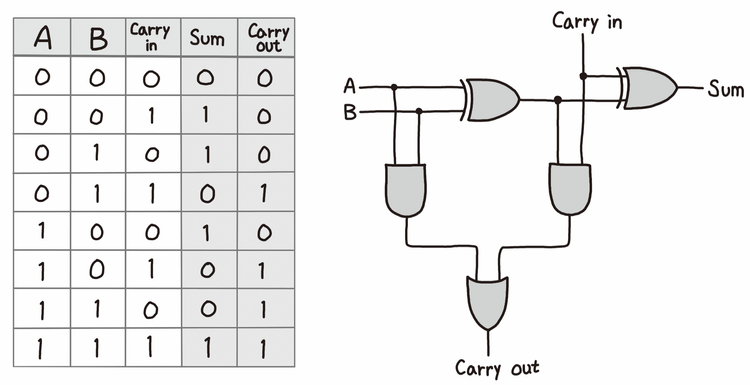
우측 전가산기 회로도는 AND 게이트 2개, XOR 게이트 2개, OR 게이트 1개로 이뤄져 있다. A와 B간의 AND 연산을 Q1, A와 B간의 XOR 연산을 Q2, Q2와 carry 간의 AND 연산을 Q3, carry와 Q2 간의 XOR 연산을 sum, Q1과 Q3간의 OR 연산을 carry로 정의해보았다.
Q1 = A & B
Q2 = A ^ B
Q3 = Q2 & carry
sum = carry ^ Q2
carry = Q1 | Q3각각의 비트는 이렇게 전가산기를 통해 합 sum을 구하는 로직으로 처리할 수 있게 되었다. 다음으로 이를 위한 전처리를 진행해본다.
MASK = 0xFFFFFFFF
a_bin = bin(a & MASK)[2:].zfill(32)a 정수를 a_bin이라는 이진수로 변경하는 데 몇가지 전처리 작업을 진행했다. 먼저 bin() 함수는 십진수 10을 이진수 0b1010으로 변환해준다.
>>> bin(10)
'0b1010'파이썬에서는 이진수로 변환되면 앞에 0b 식별자가 붙게 된다. 이는 필요 없는 부분이므로 슬라이싱 [2:]을 통해 제거해준다. 그리고 a & MASK는 앞서 살펴본 마스킹 작업이다. MASK는 비트 마스크로, 음수 처리를 위해 2의 보수로 만들어주는 역할을 한다. 여기서는 입력값을 32비트 정수로 가정했으므로 MASK는 0xFFFFFFFF로 했고, 이 값을 AND 연산하면 결과는 다음과 같이 2의 보수 값을 취하게 된다.
>>> bin(1 & MASK)
'0b1'
>>> bin(-1 & MASK)
'0b11111111111111111111111111111111'양수인 경우 마스킹을 해도 동일하지만 음수인 -1은 2의 보수에서 가장 큰 값이므로 이처럼 마스킹을 할 경우 32비트 전체가 1로 꽉 채워지는 모습을 확인할 수 있다. 다음으로 zfill(32)로 32비트 자릿수를 맞춰준다. 앞자리가 비어있으면 계산을 하기 어렵기 때문에, 모두 0으로 해서 32비트 자릿수를 다음과 같이 모두 채워준다.
>>> '1'.zfill(32)
'00000000000000000000000000000001'여기까지 전처리가 완료되면 낮은 자릿수부터 하나씩 전가산기를 통과하면서 결과를 채워나간다. 여기서는 32비트로 가정했으므로 다음과 같이 32번 반복한다.
for i in range(32):
A = int(a_bin[32-i])
B = int(b_bin[32-i])
Q1 = A & B
Q2 = A ^ B
Q3 = Q2 & carry
sum = carry ^ Q2
carry = Q1 | Q3
result.append(str(sum))
if carry == 1:
result.append('1')마지막 반복이 끝난 후 아직 carry가 남아있다면 자릿수가 하나 더 올라간 것이므로, 1을 더 추가한다. 이렇게 되면 33비트가 되겠지만 다음과 같이 마지막 마스킹 과정에서 이 값은 날아간다.
result = int(''.join(result[::-1]), 2) & MASKresult는 낮은 자릿수부터 채웠으므로 뒤집은 다음 십진수 정수로 바꿔준다. 그리고 나서 다음과 같이 마스킹을 적용하여 자릿수를 맞춰준다.
>>> int('0b10000000000000000000000000000001', 2) & MASK
1마지막으로 음수를 처리할 차례이다. 2의 보수에서 음수는 32번째 비트의 값, 즉 최상위 비트(MSB)가 1인 경우이다. 양의 정수 최댓값은 0x7FFFFFFF이므로, 만약 32번째 비트가 1이라면 이보다 큰 값이 되고, 이 경우 마스킹 값과 XOR 한 다음 NOT 처리를 해서 다시 음수로 만들어준다.
INT_MAX = 0x7FFFFFFF
...
if result > INT_MAX:
result = ~(result ^ MASK)전체 코드는 다음과 같다.
class Solution:
def getSum(self, a: int, b: int) -> int:
MASK = 0xFFFFFFFF
INT_MAX = 0x7FFFFFFF
a_bin = bin(a & MASK)[2:].zfill(32)
b_bin = bin(b & MASK)[2:].zfill(32)
result = []
carry = 0
sum = 0
for i in range(32):
A = int(a_bin[31-i])
B = int(b_bin[31-i])
Q1 = A & B
Q2 = A ^ B
Q3 = Q2 & carry
sum = carry ^ Q2
carry = Q1 | Q3
result.append(str(sum))
if carry == 1:
result.append('1')
result = int(''.join(result[::-1]), 2) & MASK
if result > INT_MAX:
result = ~(result ^ MASK)
return result
논리 회로를 직접 구현해보니 풀이가 지나치게 어렵다. 더 쉬우면서도 실용적인 풀이를 알아보자.
Solution 2 좀 더 간소한 구현
앞서 복잡하게 구현한 전가산기를 여기서는 핵심만 살려서 간단하게 동작 가능하게 해본다.
a, b = (a ^ b) & MASK, ((a & b) << 1) & MASK여기서 MASK는 2의 보수로 만들기 위한 것이고, 이전 풀이와 동일한 값이다. 여기서는 a와 b의 역할을 구분해 a에는 carry값을 고려하지 않는 a, b의 합(sum)이 담기고, b에는 자릿수를 올려가며 carry 값이 담기게 했다. 이제 마찬가지로 다음과 같이 음수에 대한 처리를 해준다.
if a > INT_MAX:
a = ~(a ^ MASK)
return a전체 코드는 다음과 같다.
class Solution:
def getSum(self, a: int, b: int) -> int:
MASK = 0xFFFFFFFF
INT_MAX = 0x7FFFFFFF
while b != 0:
a, b=(a ^ b) & MASK, ((a & b) << 1) & MASK
if a > INT_MAX:
a = ~(a ^ MASK)
return a
LeetCode 393.UTF-8 Validation
입력값이 UTF-8 문자열이 맞는지 검증하라.

Solution 1 첫 바이트를 기준으로 한 판별
UTF-8 인코딩의 구조를 구현해보고, 실제로 주어진 정수형 배열이 UTF-8 문자열이 맞는지 검증하는 문제이다. 이 문제는 UTF-8의 실제 조건을 그대로 묻는 문제이기 때문에 실용적이며, 따라서 여기서의 풀이는 실무에서도 얼마든지 활용할 수 있는 좋은 문제이다.
바이트 수 바이트 1 바이트 2 바이트 3 바이트 4
1 0xxxxxxx
2 110xxxxx 10xxxxxx
3 1110xxxx 10xxxxxx 10xxxxxx
4 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx이 표를 기준으로 첫 바이트가 1110으로 시작한다면 3바이트 문자이므로, 첫 바이트를 제외하고 뒤따르는 2바이트는 모두 10으로 시작해야 유효한 UTF-8 문자가 된다. 하지만 예제 2의 경우 세 번째 바이트가 00으로 시작하며, 따라서 정상적인 UTF-8 문자가 아니므로 False를 반환한다.
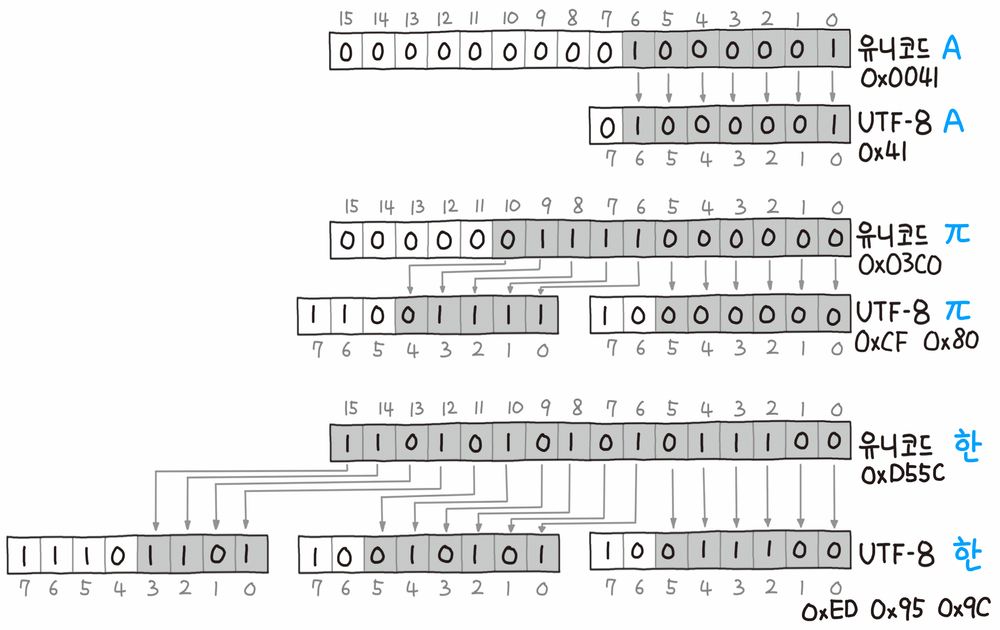
유니코드 문자의 UTF-8 인코딩은 위의 그림처럼 처리된다. 앞서 표에서 정리한 것과 동일하게 인코딩한다. 예를 들어 문자 '한'은 유니코드로 1101010101011100다. 이 값은 16비트로 표현된 문자이기 때문에, 표에 따르면 UTF-8 인코딩으로는 3바이트로 표현할 수 있다. 따라서 첫 바이트는 1110 이후 비트에 코드를 표현할 수 있으며, 나머지 바이트는 10 이후 비트에 코드를 표현해 11101101 10010101 10011100이 된다.
다음은 첫 바이트를 기준으로 판별하는 로직이다.
start = 0
while start < len(date):
first = data[start]
if (first >> 3) == 0b11110 and check(3):
start += 4
elif (first >> 4) == 0b1110 and check(2):
start += 3
elif (first >> 5) == 0b110 and check(1):
start += 2
elif (first >> 7) == 0:
start += 1
else:
return False
return Truefirst는 첫 바이트며, 만약 첫 바이트 변수가 0으로 시작한다면 1바이트 문자, 110으로 시작한다면 2바이트 문자, 1110으로 시작한다면 3바이트 문자, 11110으로 시작한다면 4바이트 문자로, 표 기준에 따라 각각 판별한다. if 조건문의 and 이후에는 각각 해당 바이트의 문자가 맞는지를 check() 함수로 판별한다. check() 함수는 다음과 같다.
def check(size):
for i in range(start+1, start+size+1):
if i>=len(data) or (data[i] >> 6) != 0b10:
return False
return Truecheck() 함수는 size를 파라미터로 받아 해당 사이즈만큼 바이트가 10으로 시작하는지를 판별한다. 앞서 첫 바이트 기준으로 만약 3바이트 문자라고 판별했다면, 나머지 2 바이트가 모두 10으로 시작하는지 판별하는 역할을 한다. 만약 하나라도 조건이 맞지 않는다면, False를 반환한다.
전체 코드는 다음과 같다.
class Solution:
def validUtf8(self, data: List[int]) -> bool:
def check(size):
for i in range(start + 1, start + size + 1):
if i >= len(data) or (data[i] >> 6) != 0b10:
return False
return True
start = 0
while start < len(data):
first = data[start]
if (first >> 3) == 0b11110 and check(3):
start += 4
elif (first >> 4) == 0b1110 and check(2):
start += 3
elif (first >> 5) == 0b110 and check(1):
start += 2
elif (first >> 7) == 0:
start += 1
else:
return False
return TrueLeetCode 191.Number of 1 Bits
부호없는 정수형을 입력받아 1비트의 개수를 출력하라.
Solution 1 1의 개수 계산
이 문제의 결과는 모두 0으로 구성된 비트들과의 해밍 거리로, 이를 해밍 가중치라고 부른다. 따라서 이 문제의 정답은 해밍 가중치의 값이라 할 수 있다.
해밍 거리는 A XOR B 이었고, 해밍 가중치는 B를 0으로 두면 된다. 위 코드에서는 y 값을 비트의 전체 길이에 맞춰 0b00000000000000000000000000000000으로 둔다.
def hammingWeight(self, n: int) -> int:
return bin(n ^ 0b00000000000000000000000000000000).count('1')32번이나 입력하는 것이 쉽지 않다. 그러나 파이썬이 자동으로 처리해주기 때문에 다음과 같이 0을 하나만 둬도 충분하다.
def hammingWeight(self, n:int) -> int:
return bin(n).count('1')
Solution 2 비트 연산
파이썬의 문자열 기능을 사용하지 않고 비트 연산으로 1비트의 개수를 구할 수 있다. 먼저 이진수의 특징부터 살펴보면, 1000에서 1을 빼면 0111이 된다. 이 두 값을 AND 연산하면 다음과 같다.
>>> bin(0b1000 & 0b0111)
'0b0'결과는 0이 된다. 다른 예로 1010에서 1을 빼면 1001이다. 이 두 값을 AND 연산한다.
>>> bin(0b1010 & 0b1001)
'0b1000'이처럼 1000만 남게 된다. 1011도 살펴보면, 마찬가지로 1을 빼면 1010이다. AND 연산을 하면 다음과 같다.
>>> bin(0b1011 & 0b1010)
'0b1010'이처럼 1을 뺀 값과 AND 연산을 할 때마다 비트가 1씩 빠지게 된다. 그렇다면 0이 될때까지 이 작업을 반복하면 전체 비트에서 1의 개수가 몇 개인지 알 수 있다는 얘기이다. 이런 특징을 활용해 다음과 같이 전체 코드를 구현할 수 있다.
class Solution:
def hammingWeight(self, n: int) -> int:
count = 0
while n:
n &= n-1
count+=1
return countn이 0이 될때까지 반복하고, 그 횟수를 반환하면 그 값이 바로 1 비트의 개수가 된다. 이 풀이는 비트 연산만으로 구현했으며, 파이썬뿐만 아니라 모든 언어에서 동일하게 활용 가능하다. 훨씬 더 범용적인 좀 더 알고리즘에 가까운 풀이라 할 수 있다.

XOR을 이용한 변수 스왑
임시 변수를 사용하지 않고 두 변수를 스왑하는 방법은 다음과 같다.
>>> x, y = 9, 4
>>> x = x + y # 13
>>> y = x - y # 9
>>> x = x - y # 4
>>> x, y
(4, 9)이와 유사하게 비트 조작으로도 임시 변수 없이 스왑이 가능하다. XOR을 이용하는 방법이다.
>>> x, y = 9, 4 # 1001, 0100
>>> x = x ^ y # 1001^0100 = 1101(13)
>>> y = x ^ y # 1101^0100 = 1001(9)
>>> x = x ^ y # 1101^1001 = 0100(4)
>>> x, y
(4, 9)덧셈, 뺄셈을 이용한 방법과 크게 다르지 않다. 우연찮게 값까지 동일하게 나왔지만, 실제로 사칙 연산과 비트 연산의 값이 동일한 것은 아니다. 그렇다면 비트 연산의 값을 먼저 살펴보자. 먼저 x^y로 두 수의 다른 부분에 대한 XOR 값을 구하고, 다시 x^y를 하면 x값이 나온다. 그 다음 이 값을 y로 할당하고, x^y를 한 번 더 계산하면 y는 x 값이므로 원래의 y값이 나오게 된다. 이제 이 값을 x로 할당하면 끝이 난다. 좀 더쉽게 나열해보면 다음과 같다.
>>> x = 10
>>> y = 40
>>> (x^y)^x
40
>>> (x^y)^y
10XOR은 순서대로 실행되므로 괄호는 필요 없지만 가독성을 위해 붙였다. x^y값에 y를 XOR 하면 x값이, 반대로 x를 XOR 하면 y값이 나온다.

