비트 조작
원래 비트를 조작하는 것은 하드웨어와 관련이 깊다. 1937년 클로드 섀넌은 전기회로 스위치의 on/off를 이용한 스위칭 회로를 연구하면서 True, False의 2개 값으로 논리 연산을 설명하는 부울대수를 회로에 적용했고, 논리 게이트를 만들어냈다. 이를 이용한 논리 회로는 현대의 모든 디지털 컴퓨터의 기본 개념이자 근간을 이루고 있다.
부울 연산자 (Boolean Operator)
부울 연산은 코드로 다음과 같이 표현할 수 있다.
>>> True and False
False
>>> True or False
True
>>> not True
FalseAND, OR, NOT은 기본 부울 연산자로, 연산들을 서로 결합하거나 조합해 다른 보조 연산을 만들어 낼 수 있다. 대표적으로 XOR이 보조 연산에 해당하며, 기본 연산들의 합으로 다음과 같이 XOR을 구성할 수 있다.
>>> x=y=True
>>> (x and not y) or (not x and y)
FalseXOR 연산은 단순한 보조 연산을 뛰어 넘어 디지털 논리 게이트에서 매우 중요한 위치를 차지한다.
비트 연산자 (Bitwise Operator)
비트 연산자는 코드로 다음과 같이 나타낼 수 있다.
>>> True & False
False
>>> True | False
True
>>> True ^ False
False
>>> ~True
-2비트 연산자 NOT인 ~는 부울 변수에 적용하면 True는 1로 간주되어 -2가 된다. 비트 연산자 NOT은 2의 보수에서 1을 뺀 값과 같기 때문이다. 따라서 십진수로 표현할 때에는 NOT x = -x - 1이 된다. 즉 NOT 1 = -1 - 1이 되어 -2가 된다.
비트 조작 퀴즈
산술 연산을 비롯한 몇 가지 비트 연산을 다음과 같이 살펴본다.
>>> bin(0b0110 + 0b0010) # 1
'0b1000'
>>> bin(0b0011 * 0b0101) # 2
'0b1111'
>>> bin(0b1101 >> 2) # 3
'0b11'
>>> bin(0b1101 << 2) # 4
'0b110100'
>>> bin(0b0101 ^ ~0b1100) # 5
'-0b1010'덧셈인 1번은 쉽다. 자릿수가 초과할 때 다음 자리로 넘겨주는 십진수의 덧셈과 동일하게 처리된다. 2번도 마찬가지로 십진수의 곱셈과 동일하다. 다만, 0은 모두 0이 되고, 1은 기존의 값이 그대로 내려온다. 2의 0011과 0101 두 이진수의 곱셈 계산 과정은 다음과 같이 나타낼 수 있다.
0011
x0101
-----
0011
0000
0011
0000
-------
1111위에서 0011과 곱하는 0101에서 0은 무시하면 되고, 1은 기존 입력값 1100에 자릿수만큼 시프팅한 결과를 더하는 것과 같다. 즉 첫 번째와 세 번째 자리가 1이므로, 첫 번째 결과는 동일한 0011, 세 번째는 두 자리를 시프팅한 001100이다. 다시 말해 0011+001100과 같다. 앞 코드부에서 3번이 바로 시프팅이다. >>은 오른쪽으로 시프팅하는 연산인데, 3번의 입력값 경우, 우측의 2칸이 시프팅되어 잘려 나가면 11만 남게 된다.
4번은 반대로 왼쪽으로 시프팅하는 연산이다. 곱셈 연산 시 사용하는 시프팅도 바로 이 좌측 시프팅이며, 지정한 수만큼인 2칸이 뒤로 추가된다. 따라서 4번의 결과는 110100이 된다. 십진수로 치면 2배씩 증가하는 것과 같다. 마찬가지로 3번은 절반씩 줄어드는 셈이다.
5번은 조금 모호한 경우이다. ~0b1100은 0b0011이 되고, 따라서 0b0101^0b0011=0b0110를 기대하고 있을 것이다. 십진수로는 6이다. 그러나 결과는 -0b1010으로 십진수로 변환해보면 -10이다. 전혀 다른 값이 되었다.
먼저 결괏값이 달라진 이유를 먼저 살펴보면, 0b1100은 십진수로 12이다. 비트 연산자 NOT 결과는 십진수로 NOT x = -x - 1이고 2의 보수에서는 1을 뺀 결과라고 앞서 얘기했다. 그렇다면 -12 - 1 = -13이 된다. -13을 2의 보수로 표현하면 111111...110011쯤이 된다. 32비트 정수형이라면 앞에 28비트 모두가 1이 된다. 앞에 값은 0b0101이므로 이 값과 함께 XOR 연산을 한 결과는 111111...110110이 된다. 2의 보수로 표현하면 이 값은 -10이 된다.
자릿수 제한 비트 연산
우리가 기대했던 결과대로 계산하는 방법이다. 우리가 기대한 것은 0b1100이 0b0011로 바뀌는 것이었지만, 이렇게 하기 위해서는 별도의 부가 작업이 필요하다. 여기서는 자릿수 만큼의 최댓값을 지닌 비트 마스크 MASK를 만들고, 그 값과 XOR을 통해 값을 만들어 본다. 먼저 MASK 값인 0b1111과 XOR 결과는 다음과 같다.
>>> bin(0b1100 ^ 0b1111)
'0b11'그렇다면 다음과 같이 MASK와 XOR 결과를 처리하는 형태로 수정할 수 있겠다.
>>> MASK = 0b1111
>>> bin(0b0101 ^ (0b1100 ^ MASK))
'0b110'이 계산 결과는 우리가 기대했던 6이다.
파이썬의 진법 표현
파이썬이 이진수(binary), 십진수(decimal), 16진수(hexadecimal)를 저장하고 표현하는 방법에 대해 알아본다. 먼저 이진수와 십진수는 다음과 같이 각각 bin()과 int()를 사용해 서로 변환할 수 있다.
>>> bin(87)
'0b1010111'
>>> int('0b1010111', 2)
87bin()을 사용하면 이진수가 문자형 0b1010111으로 반환된다. 반면 int()를 사용하면 문자형인 이진수가 십진수 숫자 정수형 87로 반환된다. 이진수임을 의미하는 접두사(Prefix) 0b는 다음과 같이 생략도 가능하다.
>>> int('1010111', 2)
87bin()을 사용해 변수에 값을 할당하면 다음과 같이 문자형이 된다.
>>> a=bin(87)
>>> a
'0b1010111'
>>> type(a)
<class 'str'>이처럼 0b1010111이라는 문자가 된다. type()을 확인해보면 문자형 클래스임을 확인할 수 있다. 만약 이진수를 문자열로 처리하지 않고 그대로 대입하면 다음과 같이 십진수 숫자형이 된다.
>>> b = 0b1010111
>>> b
87
>>> type(b)
<class 'int'>이진수를 대입한 변수 b는 십진수 숫자 87이 되고, 더 이상 이진수로 처리되지 않는다. 심지어 다음과 같이 십진수 87과 ID도 같다.
>>> id(87)
4547371104
>>> b=0b1010111
>>> b
87
>>> id(b)
4547371104따라서 이진수 0b1010111은 내부적으로 십진수 87로 변환되어 동일하게 처리된다고 볼 수 있다. 이진수를 나타내는 접두사는 0b이다. 16진수를 나타내는 접두사도 이진수의 접두사처럼 따로 존재한다. 16진수는 0x로 시작한다.
>>> hex(87)
'0x57'
>>> c = 0x57
>>> c
87
>>> id(c)
454737110416진수는 bin() 대신 hex()로 변환할 수 있으며, 마찬가지로 문자열로 처리하지 않고 그대로 대입하면 87이라는 십진수가 된다. ID 또한 16진수가 내부적으로 십진수로 변환되어 동일한 ID를 가지고 동일하게 처리된다.
2의 보수
2의 보수는 비트 조작에서 매우 중요하다. 음수 처리가 헷갈리는 편인데 이 원리를 제대로 이해한다면 전혀 어렵지 않다.
2의 보수 숫자 포맷
2의 보수는 컴퓨터가 음수를 저장하기 위해 일반적으로 취하는 여러 방법 중 하나이다. 여기서는 계산의 편의를 위해, 4비트 레지스터 머신으로 가정하고 4비트로 숫자를 표현하는 예를 살펴본다. 먼저 4비트로 표현 가능한 범위는 0000~1111로 총 16개이다. 양수만 저장한다면 0~15까지 16개를 그대로 저장하면 된다. C와 같은 언어에서는 unsigned 타입으로 선언하면 이렇게 할 수 있다. 하지만 문제는 음수도 저장해야 한다는 점이다. 따라서 절반을 쪼개서 음수 몫으로 할당하고 맨 앞 비트는 부호 비트로 사용한다. 즉 양수의 경우 0xxx를 사용하고 음수의 경우 1xxx를 사용한다.
2의 보수 숫자 포맷에서 숫자의 표현 범위는 -2^(n-1)에서 2^(n-1)-1까지가 된다. 여기서 n은 4이기 때문에 -8에서 7까지가 표현 범위이다. 4비트로 2의 보수를 표현하려면 '자릿수 제한 비트 연산'에서 사용했던 방법을 활용하면 된다. 비트 마스크 MASK를 사용하는 방식이다.
>>> MASK = 0xF
>>> bin(1 & MASK)
'0b1'
>>> bin(7 & MASK)
'0b111'
>>> bin(-8 & MASK)
'0b1000'
>>> bin(-7 & MASK)
'0b1001'
>>> bin(-1 & MASK)
'0b1111'이처럼 마스킹을 해주면 4비트로 2의 보수를 표현하는 것과 동일한 결과를 얻게 된다.
파이썬은 정확히 CPython은 임의 정밀도를 지원하기 때문에 내부적으로는 복잡한 구조로 구현되어 있다. 부호는 별도 필드로 갖고 있으며, 비트 연산이 필요한 때만 2의 보수로 변환하는 작업을 한다. 음수를 보여줄 때는 양의 정수를 표현하는 방식과 동일하게 하고 앞에 부호만 덧붙여서 보여준다.
>>> bin(-5)
'-0b101'즉 2의 보수 값을 실제로 보여주지는 않는다. 그러나 특별히 문제는 없다. 숫자를 4비트로 표현하든, 32비트로 표현하든, 비트 연산 결과는 동일하기 때문이다.
>>> 5 & -4
4이 결과를 각각 4비트 2의 보수 표현과 32비트 2의 보수 표현으로 바꿔서 비교해보면 다음과 같다.
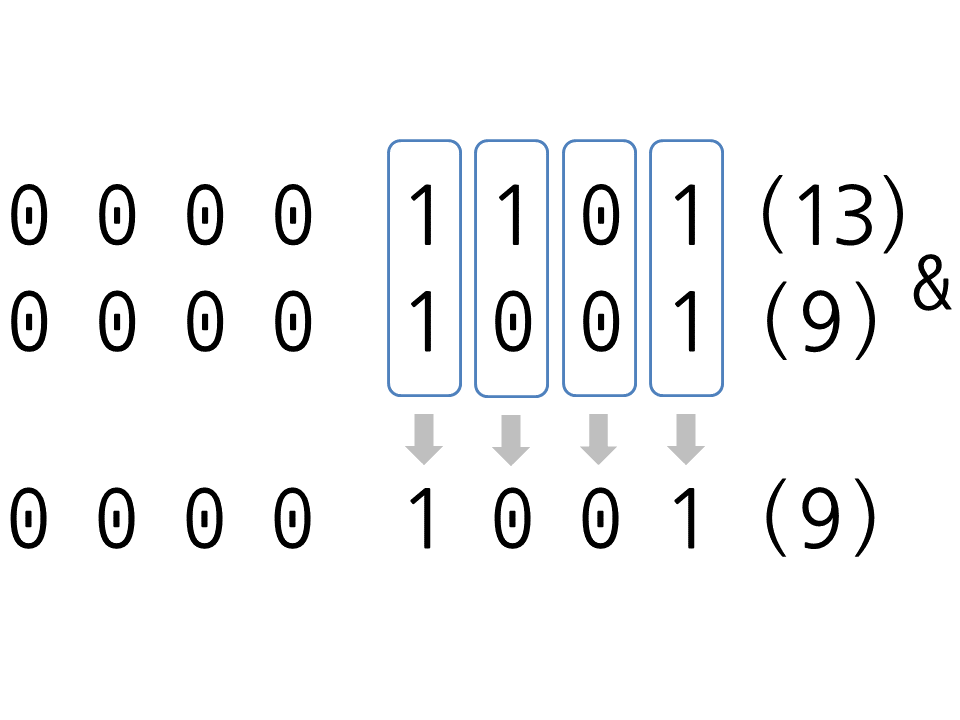
>>> bin(0b0101 & 0b1100)
'0b100'
>>> bin(0b0000000000000000000000000000101 & 0b1111111111111111111111111111100)
'0b100'이처럼 몇 비트로 표현하든 간에 AND 연산을 한 십진수 결과는 모두 4로 동일하다. 다음은 OR 연산 결과다.
>>> 5 | -4
-3
>>> bin(0b0101 | 0b1100)
'0b1101'
>>> bin(0b00000000000000000000000000000101 | 0b1111111111111111111111111111100)
'0b11111111111111111111111111111101'OR 연산도 마찬가지로 4비트로 나타내든 32비트로 나타내는 결과값은 똑같이 -3이다.
2의 보수 수학 연산
'2의 보수'라는 용어는 다소 모호함을 갖고 있다. 숫자 포맷을 쓰일 때와 수학 연산자로 쓰일 때, 2의 보수는 각기 서로 다른 의미를 지닌다. 기존에 이미 2의 보수 연산을 알고 있던 사람이라면, 앞서 숫자 포맷 의미로서의 2의 보수를 설명할 때 계속 혼동을 느꼈을 것이다. 여기서는 수학 연산의 의미로 2의 보수를 얘기할 때는 '연산'이라는 표현을 덧붙이기는 하나, 그것만으로 혼란이 가시진 않는다. '2의 보수 수학 연산'이란 무엇을 말하는 것인가?
수학적 정의를 포함해 다시 말하면, 2의 보수 수학 연산은 가산 역 연산이라고 부를 수 있다. 쉽게 설명하면 양수를 음수로, 음수를 양수로 바꾸는 작업을 말한다. 방법은 비트 연산자 NOT을 한 후에 1을 더하면 된다.
- '비트 연산자 NOT'은 2의 보수에서 1을 뺀 것이고,
- '2의 보수 수학 연산'은 비트 연산자 NOT에서 1을 더한 것이다.
즉 0110의 2의 보수 연산은 1000+1=1001이 된다. 1001의 비트 연산자 NOT은 0111-1=0110이다. 이 값은 ~1001로 표현하기도 한다.
2의 보수 연산은 정확히 양수를 음수로 또는 음수를 양수로 만들어준다. 둘을 더하면 당연히 0이 되고, 이진수로 계산할 경우 0111+1001=10000로 자릿수 오버플로가 발생하는데, 4비트 연산이므로 초과한 자릿수는 무시하며 따라서 0000, 즉 0이 된다.
비트 연산자 NOT
비트 연산자 NOT은 기준 비트 내에서 정확히 1을 0으로, 0을 1로 바꿔준다. 4비트라 가정할 때 0111은 1000이며 2의 보수 포맷에서는 0111은 7, 1000은 -8로 NOT x = -x - 1이 된다.
>>> bin(0b0101 ^ ~0b1100)
'-0b1010'이 값이 0b0110이 아닌 이유는 여기서 입력값이 4비트 포맷이 아니라는 점 때문이다. 만약 4비트 머신이라면 0b1100이 음수 -4여야 하는데, 실제로는 이 값을 양수 12로 가정했으므로 이미 오버플로가 발생한 상태라 전제조건에 문제가 있었던 셈이다. 이 문제는 다음과 같이 8비트 포맷 또는 좀 더 큰 형태로 바꿔야 제대로 계산할 수 있다.
>>> bin(0b00000101 ^ ~0b00001100)
'-0b1010'8비트 포맷으로 바꿔서 적용하였다. 계산 결과는 동일하다. 이번에는 두 번째 값을 직접 먼저 계산한 결과를 두고 다시 계산해보자.
>>> bin(0b00000101 ^ 0b11110011)
'0b11110110'여기서는 두 번째 값을 2의 보수로 직접 만들어 NOT 연산자부터 먼저 계산해봤다. 결과는 1111 0011이고 이 값과 XOR한 최종 결과는 1111 0110이다. 2의 보수이므로, 이 값은 -10이다. 앞서 결과였던 -0b1010도 -10이므로 동일하다. 이제 정확하게 계산할 수 있게 되었다. 8비트가 아니라 16비트 또는 그 이상이라도, 결과는 마찬가지로 다음과 같이 동일하다.
>>> bin(0b0000000000000101 ^ ~0b0000000000001100)
'-0b1010'