
이진 검색 (Binary Search)
이진 검색에 대해 조금 더 알아보았다.
LeetCode 349.Intersection of Two Arrays
두 배열의 교집합을 구하라.

우선 이진 검색을 이용하여 문제를 혼자 풀어보았다. 성능을 위해 길이가 더 짧은 배열을 순회하며 길이가 더 긴 배열을 이진 검색하며 해당 수가 있을 경우 결과 집합에 추가하도록 하였다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
if len(nums2)>len(nums1):
nums1, nums2=nums2, nums1
nums1.sort()
answer=set()
for i in range(len(nums2)):
left, right=0, len(nums1)-1
while left<=right:
mid=(left+right)//2
if nums1[mid]<nums2[i]:
left=mid+1
elif nums1[mid]>nums2[i]:
right=mid-1
else:
answer.add(nums1[mid])
break
return answer
파이썬에서 제공하는 집합의 연산을 사용해서도 풀어보았다. nums1과 nums2를 집합으로 변경한 후 두 집합의 교집합을 반환하도록 하였다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
n1=set(nums1)
n2=set(nums2)
return n1 & n2
Solution 1 브루트 포스로 계산
이 문제는 이진 검색과 투 포인터 등 다양한 풀이법을 시도할 수 있다. 먼저 가장 간단하고 직관적인 브루트 포스부터 풀이해본다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
result: Set = set()
for n1 in nums1:
for n2 in nums2:
if n1==n2:
result.add(n1)
return result
O(n^2)으로 반복하면서 일치하는 경우 무조건 추가한다. 데이터 타입은 집합이기 때문에 속도는 느리긴 해도 중복된 값은 알아서 잘 처리해준다.
Solution 2 이진 검색으로 일치 여부 판별
한쪽은 순서대로 탐색하고 다른 쪽은 정렬해서 이진 검색으로 값을 찾으면 검색 효율을 획기적으로 높일 수 있다. 이 경우 시간 복잡도는 O(n log n)이 된다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
result: Set=set()
nums2.sort()
for n1 in nums1:
i2=bisect.bisect_left(nums2, n1)
if len(nums2)>0 and len(nums2)>i2 and n1==nums2[i2]:
result.add(n1)
return result
Solution 3 투 포인터로 일치 여부 판별
이 문제는 양쪽 다 정렬하여 투 포인터로 풀이할 수도 있다. 이는 병합 정렬 시 마지막에 최종 결과를 비교하는 과정과 유사하다. 다만 일치하는 값을 판별한다는 차이만 있을 뿐이다. 이 경우 각각 정렬에 2O(n log n), 비교에 O(2n)이 소요되므로 O(n log n)에 풀이가 가능하다.
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
result: Set = set()
nums1.sort()
nums2.sort()
i=j=0
while i<len(nums1) and j<len(nums2):
if nums1[i]>nums2[j]:
j+=1
elif nums1[i]<nums2[j]:
i+=1
else:
result.add(nums1[i])
i+=1
j+=1
return result이 경우 정렬을 제외하면 비교에 따른 시간 복잡도는 상수항을 제외하여 O(n)에 불과하다.

O(n^2)인 부루트 포스의 풀이가 가장 느리고, 각각 O(n log n)인 이진 검색과 투 포인터는 비슷한 성능을 보인다.
LeetCode 167.Two Sum II - Input Array Is Sorted
정렬된 배열을 받아 덧셈하여 타겟을 만들 수 있는 배열의 두 숫자 인덱스를 리턴하라.
*주의: 이 문제에서 배열은 0이 아닌 1부터 시작하는 것으로 한다.
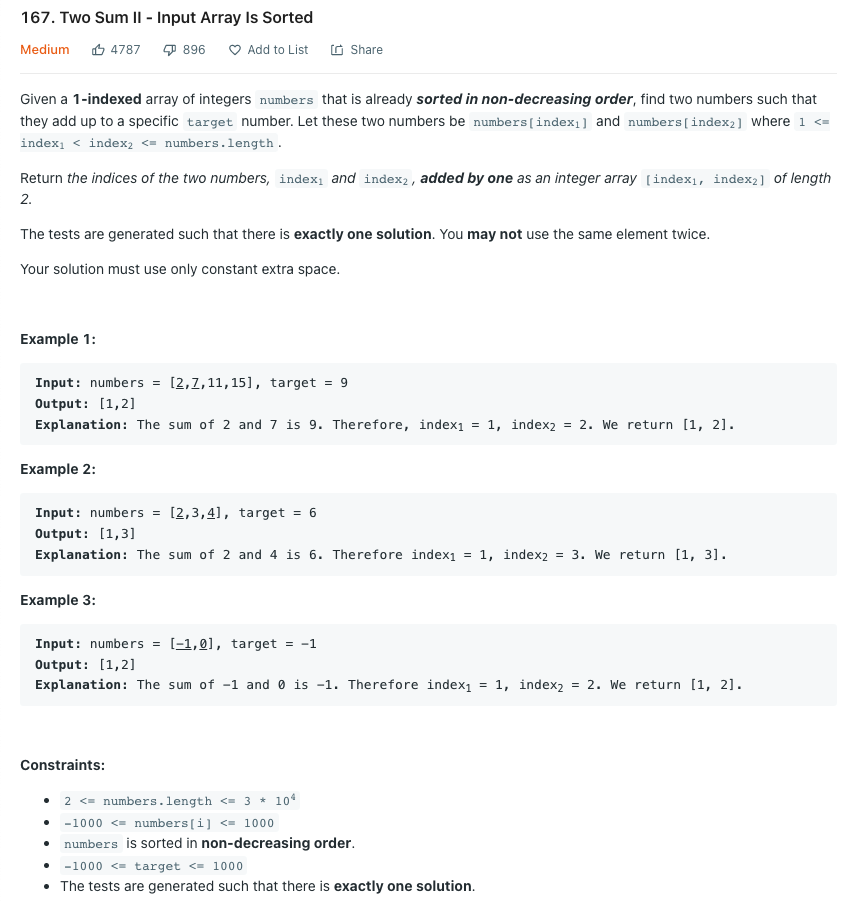
우선 투 포인터를 이용하여 혼자 풀어보았다. i는 가장 앞에서부터, j는 가장 뒤에서부터 시작하였다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
i, j=0, len(numbers)-1
while i<len(numbers) and j>=0:
if numbers[i]+numbers[j]>target:
j-=1
elif numbers[i]+numbers[j]<target:
i+=1
else:
return [i+1, j+1]
Solution 1 투 포인터
이 문제는 입력 배열이 정렬되어 있는 가정이 있기 때문에 투 포인터로 해결할 수 있다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left, right=0, len(numbers)-1
while not left==right:
if numbers[left]+numbers[right]<target:
left+=1
elif numbers[left]+numbers[right]>target:
right-=1
else:
return [left+1, right+1]이 풀이는 내가 혼자 작성했던 풀이와 거의 유사하다. O(n)에 풀이되는 코드이다.

Solution 2 이진 검색
이번에는 이진 검색으로 풀어본다. 현재 값을 기준으로 나머지 값이 맞는 지 확인하는 형태의 이진 검색 풀이를 시도해볼 수 있다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
left, right=k+1, len(numbers)-1
expected=target-v
while left<=right:
mid=left+(right-left)//2
if numbers[mid]<expected:
left=mid+1
elif numbers[mid]>expected:
right=mid-1
else:
return k+1, mid+1이 경우 이진 검색 log n을 n번 반복하므로 시간 복잡도는 O(n log n)이 된다. 이 두가지 방식만 놓고 본다면 투 포인터가 O(n)으로 이진 검색 풀이 O(n log n)에 비해 더 빠르게 실행된다. 그렇다면 이진 검색에 bisect 모듈을 사용해 좀 더 속도를 높일 수 있을까?

Solution 3 bisect 모듈 + 슬라이싱
bisect 모듈을 사용해 이진 검색을 구현해본다. 이렇게 하면 이진 검색 알고리즘을 직접 구현할 필요가 없기 때문에 코드도 한결 깔끔해진다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
left, right=k+1, len(numbers)-1
expected=target-v
i=bisect.bisect_left(numbers[k+1:], expected)
if i<len(numbers[k+1:]) and numbers[i+k+1]==expected:
return k+1, i+k+2left, right 변수도 필요 없고, 예상대로 코드는 깔끔해졌지만 실행 속도가 매우 느려졌다.

Solution 4 bisect 모듈 + 슬라이싱 최소화
이전 풀이에서 슬라이싱을 무리하게 적용하여 성능이 안좋았던 것 같아 nums 변수에 한 번만 사용해 담아두는 형태로 개선을 시도했다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
expected=target-v
nums=numbers[k+1:]
i=bisect.bisect_left(nums, expected)
if i<len(nums) and numbers[i+k+1]==expected:
return k+1, i+k+2
속도가 조금 개선되었다. 그래도 많이 느리기 때문에 더 개선해야 한다.
Solution 5 bisect 모듈 + 슬라이싱 제거
bisect 모듈의 공식 문서를 보면 다음과 같이 기본 파라미터 외에도 여러 추가 파라미터가 있는 것을 볼 수 있다.
bisect.bisect_left(a, x, lo=0, hi=len(a))이 문서를 참고하여 왼쪽 범위를 제한하는 파라미터인 lo를 찾아냈고, 이 값을 지정하는 것으로 풀이를 진행하였다.
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
for k, v in enumerate(numbers):
expected=target-v
i=bisect.bisect_left(numbers, expected, k+1)
if i<len(numbers) and numbers[i]==expected:
return k+1, i+1
투 포인터의 성능과 같아졌다. 슬라이싱은 편리하고 빠른 모듈이지만, 이처럼 무분별하게 남용하면 속도 저하의 주범이 되기도 한다. 경우에 따라서는, 꼭 필요한 곳에만 적절히 사용해야 실행 속도를 최적화할 수 있다.
LeetCode 240.Search a 2D Matrix II
mxn 행렬에서 값을 찾아내는 효율적인 알고리즘을 구현하라. 행렬은 왼쪽에서 오른쪽, 위에서 아래 오름차순으로 정렬되어 있다.

Solution 1 첫 행의 맨 뒤에서 탐색
이 문제는 열을 기준으로 이진 검색을 수행한 다음, 찾아낸 값을 기주능로 해당 위치의 각행을 기준으로 다시 이진 검색을 수행하면 해결할 수 있을 것 같다. 그러나 첫 번째 이진 검색은 쉽게 할 수 있지만, 두 번째 이진 검색은 생각보다 효율적으로 풀이하기가 쉽지 않다. 왜냐면 각 행에서 특정 인덱스를 기준으로 값을 추출해오는데 적지 않은 연산이 필요하기 때문이다. 예를 들어 각 행의 세 번째 인덱스를 가져온다고 해보자. 이 경우 matrix[n][3]과 같이 각 행에 대한 값 추출 작업이 필요하므로 결국 O(n)이 필요하며, 이진 검색으로 인한 O(log n) 성능을 누릴 수 없다. 또한 첫 번째 행을 찾아낸다 해도 그게 정확한지 확신할 수 없다. 얼마든지 다른 행에 정답이 있을 수 있기 때문이다.
따라서 여기서는 조금 더 단순한 방법을 사용한다. 첫 행의 맨 뒤 요소를 택한 다음, 타겟이 이보다 작으면 왼쪽으로, 크면 아래로 이동하게 하는 방법이다. 행렬은 왼쪽에서 오른쪽, 위에서 아래로 오름차순으로 정렬되어 있기 때문에, 작으면 왼쪽, 크면 아래로 이동하면 원하는 위치에 어렵지 않게 도달할 수 있을 것이다.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
if not matrix:
return False
row=0
col=len(matrix[0])-1
while row<=len(matrix)-1 and col>=0:
if target==matrix[row][col]:
return True
elif target<matrix[row][col]:
col-=1
elif target>matrix[row][col]:
row+=1
return False
Solution 2 파이썬다운 방식
이 문제는 파이썬다운 방식으로 한 줄 풀이도 가능하다. 파이썬 내부적으로 행렬에 값이 존재하는지 여부를 위에서부터 차례대로 한 줄씩 탐색하게 된다.
class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
return any(target in row for row in matrix)
이 문제는 이진 검색으로 풀이가 어렵고, 조금 다른 방식을 사용해야 했다. 이처럼 예상과 달리 다른 방법으로 풀리는 경우가 있으므로, 실제 코딩 테스트 시에도 예상 방식대로 풀이가 되지 않는다면 그 방식에 너무 많은 시간을 허비하지 않도록 유의해야 한다.
문법: any()와 all() 함수
>>> any([True, False, False])
Trueany()는 포함된 값 중 어느 하나가 참이라면 항상 참으로 출력한다. 논리 연산의 OR과 비슷하다.
>>> True or False or False
True반면 all()이라는 함수도 있다. 이 함수는 모든 값이 참이어야 True를 출력한다.
>>> all([True, False, False])
False
>>> all([True, True, True])
True이처럼 all()은 논리 연산의 AND와 유사하다.
>>> True and True and True
Trueany()와 all() 두 함수 모두 유용하게 활용할 수 있는 파이썬 내부 함수들이므로, 잘 기억하는 것이 좋다.
