[ Python_Algorithm ] 트리 (Tree) 1

황승환·2022년 2월 15일

Python_Algorithm

목록 보기

17/32

트리 (Tree)

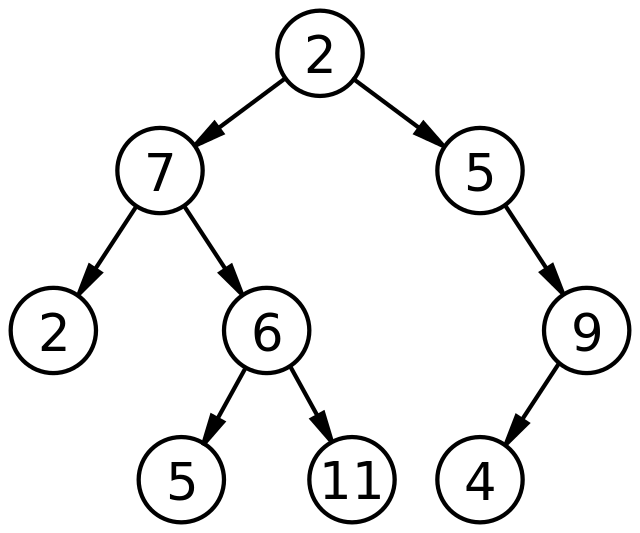
트리는 계층형 트리 구조를 시뮬레이션 하는 추상 자료형(ADT)으로, 루트 값과 부모-자식 관계의 서브 트리로 구성되며, 서로 연결한 노드의 집합이다.

트리는 나무의 뿌리에서 위로 뻗어나가는 형상처럼 생겨서 트리라는 명칭이 붙었고, 트리 구조를 구현할 때는 나무의 형상과는 반대 방향으로 표현한다. 트리의 속성 중 중요한 것은 재귀로 정의된 자기 참조 자료구조라는 것이다. 이는 자식도 트리이고, 그 자식도 트리, 즉 여러 개의 트리가 쌓아 올려져 큰 트리가 된다는 의미이다. 흔히 서브트리로 구성된다고 표현한다.

트리의 각 명칭

트리는 항상 루트(Root)에서부터 시작한다.
루트는 자식(Child) 노드를 가지며 간선(Edge)으로 연결되어 있다.
자식 노드의 개수를 차수(Degree)라고 한다.
자신을 포함한 모든 자식 노드의 개수를 크기(Size)라고 한다.
현재 위치에서부터 리프(Leaf)까지의 거리를 높이(Height)라고 한다.
깊이(Depth)는 루트에서부터 현재 노드까지의 거리이다.
레벨은 0에서부터 시작한다.
트리는 항상 단방향이기 때문에 간선의 화살표는 생략 가능하다.

그래프 vs 트리

그래프의 트리의 차이점에 대한 질문을 면접에서 받을 가능성이 있다. 그래프와 트리의 무엇보다도 가장 두드러지는 큰 차이점은 다음과 같다.
"트리는 순환 구조를 갖지 않는 그래프이다."
핵심은 순환 구조가 아니라는 데에 있다. 트리는 특수한 형태의 그래프의 일종으로 크게 그래프의 범주에 포함된다. 그러나 트리는 그래프와 달리 어떠한 경우에도 한번 연결된 노드가 다시 연결되지 않는다. 이 외에도 그래프는 단방향과 양방향을 모두 가리킬 수 있는 반면, 트리는 부모에서 자식으로의 단방향만 가능하다. 그리고 트리는 하나의 부모 노드를 갖게 되고, 루트 또한 하나이다.

이진 트리

이진트리의 정의는 매우 쉽다. 트리 중에서도 가장 널리 사용되는 트리 자료구조는 이진 트리와 이진 탐색 트리이다. 실제로 인터뷰 시에도 가장 자주 질문을 받게 되는 기본적인 트리 형태이다.

먼저 각 노드가 m개 이하의 자식을 갖고 있을 경우에는 m-ary 트리(다항 트리 or 다진 트리)라고 한다. m이 2일 경우, 즉 모든 노드의 차수가 2 이하일 경우에는 특별히 이진 트리라고 구분해서 부른다. 이진트리는 왼쪽 오른쪽 최대 2개의 자식을 갖는 매우 단순한 형태로, 다진 트리에 비해 훨씬 간결할 뿐만 아니라 여러 가지 알고리즘을 구현하는 일도 좀 더 간단하게 처리할 수 있다. 그래서 대체로 트리라고 하면 특별한 경우가 아니라면 대부분 이진 트리를 일컫는다.

이진 트리의 유형을 보면 다음과 같다.

정 이진 트리(Full Binary Tree)
완전 이진 트리(Complete Binary Tree)
포화 이진 트리(Perfect Bianry Tree)

정 이진 트리(Full Binary Tree)

모든 노드가 0개 또는 2개의 자식 노드를 가진다.

완전 이진 트리(Complete Binary Tree)

마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있다.

포화 이진 트리(Perfect Bianry Tree)

모든 노드가 2개의 자식 노드를 가지고 있으며 모든 리프 노드가 동일한 깊이 또는 레벨을 가진다. 문자 그대로 완벽한 유형의 트리이다.

LeetCode 104.Maximum Depth of Binary Tree

이진 트리의 최대 깊이를 구하라.

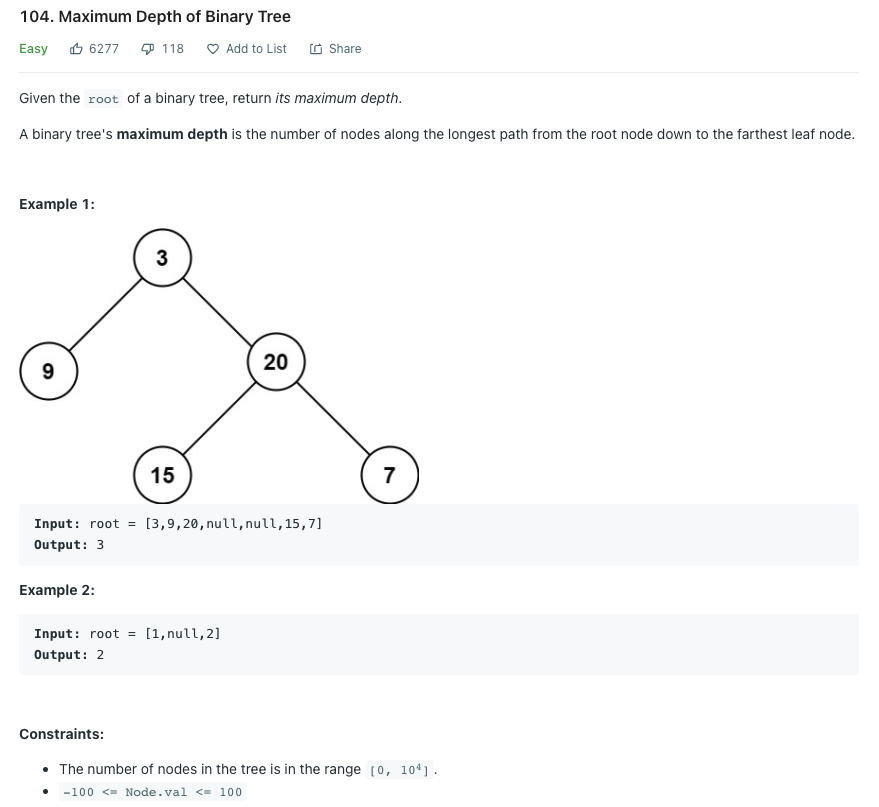
Solution 1 반복 구조로 BFS 풀이

깊이를 측정할 수 있는 여러 가지 방법 중 하나는 BFS를 통해 해결하는 것이다. BFS는 재귀가 아닌 반복 구조로 풀이할 수 있다. BFS는 큐를 사용하므로 다음과 같이 큐를 선언해준다.

def maxDepth(self, root:TreeNode) -> int:
    ...
    queue = collections.deque([root])
    depth = 0
    
    while queue:
        ...
    
    return depth

큐를 선언하고 반복 구조도 구성하여 BFS 반복을 이용해 풀이할 구조를 잡았다. 파이썬에서 큐는 일반적인 리스트로도 모든 연산이 가능하지만 데크 자료형을 사용하면 이중 연결 리스트로 구성되어 있기 때문에 스택 연산을 모두 자유롭게 활용 가능할 뿐만 아니라 양방향 모두 O(1)에 추출할 수 있기 때문에 좋은 성능을 보인다.

큐 변수에는 현재 깊이 depth에 해당되는 모든 노드가 들어있고, queue.popleft()로 하나씩 꺼내며 cur_root.has_child()로 자식 노드가 있는지 여부를 판별한 후 자식 노드를 다시 큐에 삽입한다.

동일한 큐에 삽입을 하면 행여나 자식 노드가 부모 노드와 섞이진 않을까 생각할 수 있다. 물론 섞이게 될 것이다. 그러나 이 반복문에서는 자식 노드가 추출되는 일이 없다. 그 이유는 처음 for문 진입 시 부모 노드의 길이만큼 반복되도록 선언했기 때문이다. 따라서 부모 노드가 모두 추출된 이후에는 for문을 빠져나가게 되고 다시 한바퀴 돌아 while queue 구문에서 이번에는 다음 번 깊이의 노드 반복이 진행될 것이다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root is None:
            return 0
        queue = collections.deque([root])
        depth = 0
        
        while queue:
            depth += 1
            for _ in range(len(queue)):
                cur_root = queue.popleft()
                if cur_root.left:
                    queue.append(cur_root.left)
                if cur_root.right:
                    queue.append(cur_root.right)
        return depth

LeetCode 543.Diameter of Binary Tree

이진 트리에서 두 노드 간 가장 긴 경로의 길이를 출력하라.

Solution 1 상태값 누적 트리 DFS

가장 긴 경로를 찾는 방법은 가장 밑단, 즉 리프 노드까지 탐색한 다음 부모로 거슬러 올라가면서 각각의 거리를 계산해 상태값을 업데이트하면서 누적하는 방법으로 풀이하는 것이다.

존재하지 않는 노드에도 -1이라는 값을 부여하고, 거슬러 올라가면 최종 루트에서 상태값은 2, 거리는 3이 된다. 정답은 거리인 3이 된다. 상태값은 리프 노드에서 현재 노드까지의 거리이다. 거리는 왼쪽 자식 노드의 상태값과 오른쪽 자식 노드의 상태값의 합에 2를 더한 값이 된다. 다시 정리하면 최종적으로 거리는 왼쪽 자식 노드의 리프 노드에서 현재 노드까지의 거리와 오른쪽 자식 노드의 리프 노드에서 현재 노드까지의 거리의 합에 2를 더한 값과 같다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    longest: int = 0
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        def dfs(node: TreeNode) -> int:
            if not node:
                return -1
            left=dfs(node.left)
            right=dfs(node.right)

            self.longest=max(self.longest, left+right+2)
            return max(left, right)+1
        dfs(root)
        return self.longest

문법: 중첩 함수에서 클래스 변수를 사용한 이유

위의 풀이에서 중첩 함수를 사용할 때 longest 변수를 함수 내에 선언하지 않고 클래스 변수로 선언하여 self.longest 형태로 사용한 것을 볼 수 있다. 중첩 함수는 부모 함수의 변수를 자유롭게 읽어들일 수 있다. 그러나 중첩 함수에서 부모 함수의 변수를 재할당하게 되면 참조 ID가 변경되며 별도의 로컬 변수로 선언된다. longest 변수에 값을 재할당하는 부분에서 self.longest를사용하여 부모 함수의 변수를 그대로 사용한 것이 아닌 함수 바깥에서 클래스 변수로 선언 후 사용한 것이다.

만약 longest의 값이 숫자나 문자가 아니라 리스트나 딕셔너리였다면 append() 등을 통해 재할당 없이 조작할 수 있다. 그러나 숫자나 문자의 경우에는 불변객체이므로 중첩 함수 내에서는 값을 변경할 수 없다. 이 때문에 클래스 변수를 사용하였다.