트리 (Tree)

트리에 대해 조금 더 알아보았다.

LeetCode 687.Longest Univalue Path

동일한 값을 지닌 가장 긴 경로를 찾아라.

Solution 1 상태값 거리 계산 DFS

트리의 리프 노드까지 DFS로 탐색해 내려가고 값이 일치할 경우 거리를 차곡차곡 쌓아 올려가며 백트래킹하는 방식으로 풀이가 가능하다. DFS 재귀 탐색은 다음과 같이 작성해야 한다.

def dfs(node: TreeNode):
    ...
    left=dfs(node.left)
    right=dfs(node.right)

이렇게 재귀 호출로 내려가면 left, right는 각각 리프 노드에 이르러서 값을 반환받게 된다. 더 이상 존재하지 않는 노드까지 내려가게 되면 다음과 같은 형태로 값을 반환한다.

if node is None:
    return 0

존재하지 않는 노드까지 내려가게 되면 거리 0을 반환한다. 이제 이 값이 점점 백트래킹을 통해 커질 것이다. 이 문제는 동일값의 여부를 판단하여 거리를 계산하는 문제이기 때문에 다음과 같이 자식 노드가 동일한 값인지 확인하는 과정이 필요하다.

if node.left and node.left.val==node.val:
    left+=1
else:
    left=0
if node.right and node.right.val==node.val:
	right+=1
else:
	right=0

왼쪽 오른쪽 자식 노드를 각각 확인하며 현재 노드, 즉 부모 노드와 동일한 경우 각각 거리를 1 증가한다. 결과는 왼쪽 오른쪽 자식 노드 간 거리의 합으로 취한다.

result=max(result, left+right)

합이 가장 큰 값을 최종 결과로 한다. 이제 다음 번 백트레킹 시 계산을 위해 상태값을 셋팅해서 부모 노드로 올려야 한다. 다음과 같이 부모 노드를 위해 현재까지의 거리를 반환한다.

return max(left, right)

여태 합의 최대값을 계산하였기 때문에 상태값도 합으로 반환해야 할 것 같지만 이 문제에서는 양쪽 노드를 동시에 연결할 수 없고, 단방향이기 때문에 양쪽 자식 중 하나의 자식만을 택할 수 있으며, 이는 트리의 특징이기도 하다. 따라서 둘 중 큰 값을 상태값으로 반환한다. 한 군데만 방문한다면 더 큰 쪽을 방문하는 것이 더 낫기 때문이다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    result: int=0
    def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
        def dfs(node: TreeNode):
            if node is None:
                return 0
            left=dfs(node.left)
            right=dfs(node.right)
            if node.left and node.left.val == node.val:
                left+=1
            else:
                left=0
            if node.right and node.right.val == node.val:
                right+=1
            else:
                right=0
            self.result = max(self.result, left+right)
            return max(left, right)
        dfs(root)
        return self.result

LeetCode 226.Invert Binary Tree

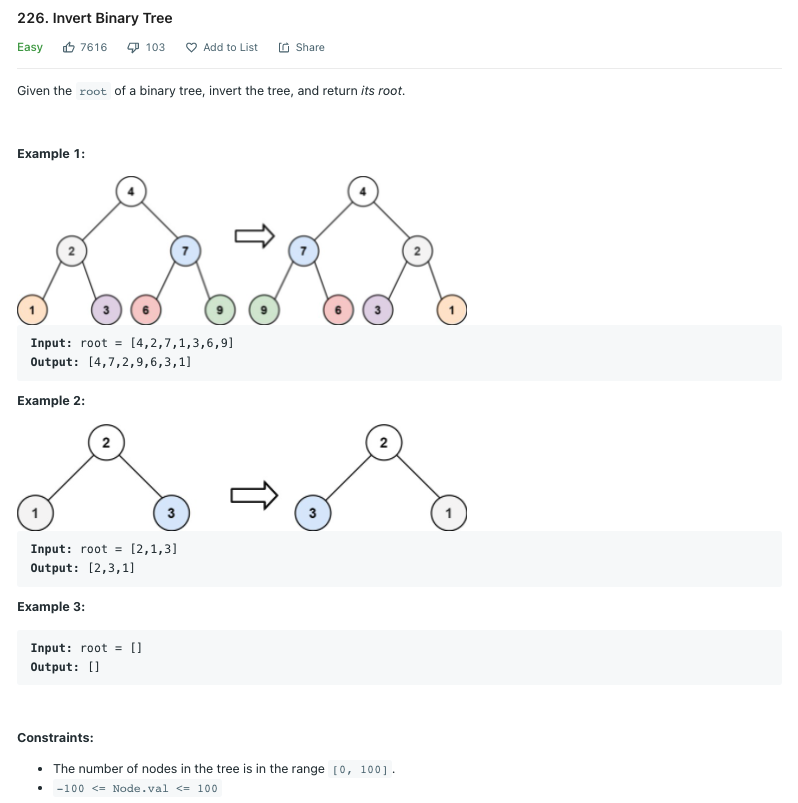
Solution 1 파이썬다운 방식

이 문제는 파이썬다운 방식으로 매우 짧고 간결하게 해결할 수 있다. 우선 이번 코드는 재귀함수를 통하여 리프 노드인 9에서 처음으로 스왑이 발생한다. 그리고 왼쪽으로 가서 3과 1 간의 스왑이 발생하게 된다. 마지막으로는 2와 7이 스왑되어 끝이 난다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if root:
            root.left, root.right=self.invertTree(root.right), self.invertTree(root.left)
            return root
        return None

재귀 함수를 이용하여 매우 간단하게 작성하였다.

Solution 2 반복 구조로 BFS

이번에는 간단한 BFS를 이용하여 풀이해보았다. BFS대로 큐에 하나씩 노드를 담은 뒤에 매 반복마다 left와 right를 바꿔주고 반복 종료 전에 left와 right를 큐에 넣어주는 방식으로 하여 모든 노드에 접근하여 반전시키도록 작성하였다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        q=collections.deque([root])
        while q:
            node=q.popleft()
            if node:
                node.left, node.right=node.right, node.left
                q.append(node.left)
                q.append(node.right)
        return root

앞에서 풀어보았던 재귀 풀이는 리프 노드까지 내려간 뒤에 백트레킹을 통해 스왑하는 상향 방식이고, 이번 풀이 방식은 부모 노드부터 스왑하면서 계속 아래로 내려가는 하향 방식이다.

Solution 3 반복 구조로 DFS

이 풀이 방법은 BFS와 매우 유사하지만 큐 대신 스택을 사용하여 뒤에서부터 꺼내어 스왑하는 방식으로 구현되었다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        stack=collections.deque([root])
        while stack:
            node=stack.pop()
            if node:
                node.left, node.right=node.right, node.left
                stack.append(node.left)
                stack.append(node.right)
        return root

Solution 4 반복 구조로 DFS 후위 순회

Solution 3 또한 전위 순회 형식으로 처리되었다. 이번에는 DFS를 통한 후위 순회 형식으로 풀이해보았다. 탐색의 순서만 바뀌게 될 뿐 아무런 문제도 되지 않는다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        stack=collections.deque([root])
        while stack:
            node=stack.pop()
            if node:
                stack.append(node.left)
                stack.append(node.right)
                
                node.left, node.right=node.right, node.left
        return root

LeetCode 617.Merge Two Binary Trees

두 이진 트리를 병합하라. 중복되는 노드는 값을 합산한다.

Solution 1 재귀 탐색

이번에는 간단한 재귀 탐색을 통해 해결해보았다. 각각 이진 트리의 루트부터 시작하여 합쳐 나간다. 좌, 우 자식 노드 또한 병합될 수 있도록 각 트리 자식 노드를 재귀 호출한다. 만약 어느 한쪽에 노드가 존재하지 않을 경우 존재하는 노드만 반환하고 더 이상 재귀호출을 진행하지 않는다. 만약 양쪽 노드가 모두 존재하지 않는다면 None이 반환될 것이다. 이 풀이 방법은 리프노드부터 탐색하는 후위 순회 방식이다.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        if root1 and root2:
            node=TreeNode(root1.val + root2.val)
            node.left=self.mergeTrees(root1.left, root2.left)
            node.right=self.mergeTrees(root1.right, root2.right)
            return node
        else:
            return root1 or root2