백준 11057 오르막 수 (C++)

11057번: 오르막 수

dp를 이용한 문제이다. 점화식을 먼저 생각해 봐야한다. 아래 표를 통해 도출해볼 수 있다.

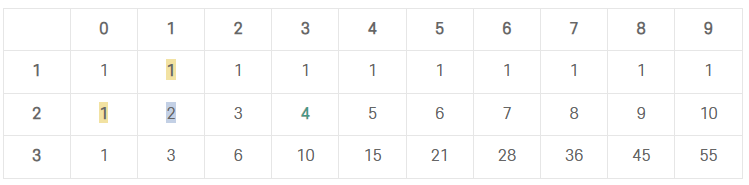
행은 N에, 열은 맨 앞자리 수에 해당한다. 에를 들어 dp[2][9]일 경우, 길이가 2이고 맨 앞자리가 9인 오르막 수의 갯수가 10개에 해당한다. 이를 점화식으로 나타내면 dp[i][j] = dp[i][j-1] + dp[i-1][j] 가 된다. 반복문을 통해 모든 dp를 구하고 dp[N]에 해당하는 값들을 더해 나눈 나머지를 출력해주었다.
점화식을 생각해내는 데 시간이 오래 걸렸다.

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

int N, res = 0;
int dp[1001][10];

void solution() {
	for (int i = 0; i < 10; i++) {
		dp[1][i] = 1;
	}

	for (int i = 2; i <= N; i++) {
		for (int j = 0; j < 10; j++) {
			if (j == 0) {
				dp[i][j] = 1;
				continue;
			}

			dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
			dp[i][j] %= 10007;
		}
	}

	for (int i = 0; i < 10; i++) {
		res += dp[N][i];
	}

	cout << res % 10007;
}

int main(){
	ios_base::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	cin >> N;

	solution();
	
	return 0;
}