백준 12865 평범한 배낭 (C++)

12865: 평범한 배낭

아주 유명한 0-1 배낭 문제이다. dp를 활용하여 갯수와 무게 총합마다 총 가치를 구해주는 방식을 사용한다. 문제를 푸는 핵심으로 점화식이 중요하다. i 는 물건 번호, j 는 현재 배낭 무게이다.
dp[i][j] = max(dp[i-1][j], dp[i-1][j-W[i]] + V[i])

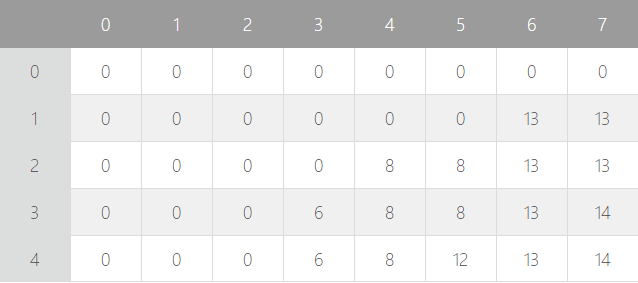
위 그림은 점화식을 이용하여 문제 예제를 표로 나타낸 것이다.
dp[3][7]을 살펴보면, dp[2][7]과 dp[2][7-(3번 물건 무게) + v[3]] 중 큰 값을 가지게 된다. dp[3][4]는 6이고 v[3]은 8이므로 dp[2][7]은 13, dp[3][7]은 14이므로 dp[3][7]은 14를 가지게 된다. 이를 반복하여 최종 값을 구할 수 있게 된다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int N, K;
vector<pair<int, int>> v;
int dp[101][100001];

void solution() {
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= K; j++) {
            if (j - v[i].first >= 0) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i].first] + v[i].second);
            }
            else
                dp[i][j] = dp[i - 1][j];
        }
    }

    cout << dp[N][K];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    cin >> N >> K;
    
    v.push_back({ 0,0 });  // 안쓰는 값
    for (int i = 0; i < N; i++) {
        int a, b;
        cin >> a >> b;
        v.push_back({ a,b });
    }

    solution();

    return 0;
}