트리 구조란?
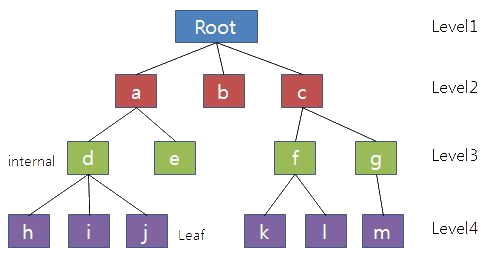
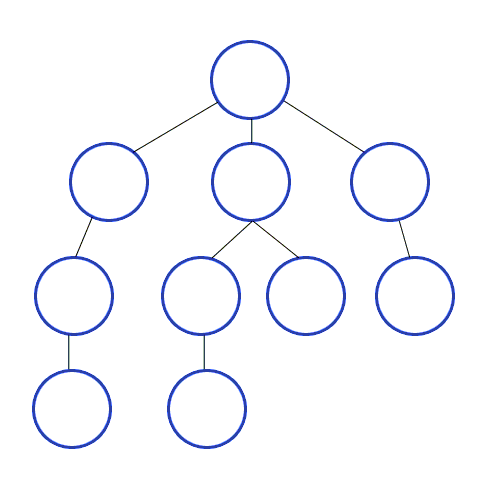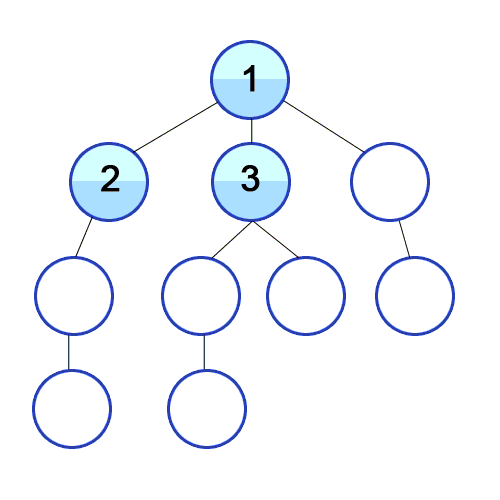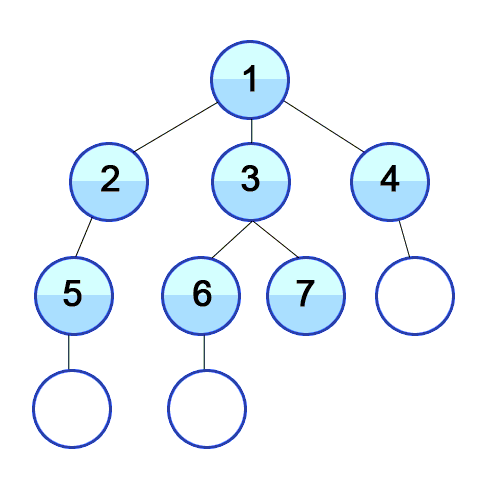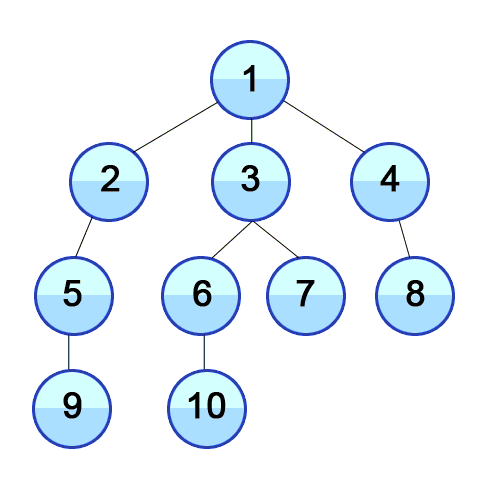
오늘은 트리 구조에 대해서 알아보겠습니다. 트리라는 이름은 나무와 닮아있어서 붙은 이름입니다. 위의 그림을 거꾸로 보면 뿌리, 줄기, 잎을 가진 나무의 형상과 비슷하죠. 트리 구조에서도 뿌리, 줄기, 잎에 해당하는 노드들이 있습니다.
맨 위의 노드를 root, 맨 아래의 노드를 leaf , 그 중간에 있는 노드들을 내부 노드라고 합니다. 노드와 노드를 이어주는 다리를 branch 혹은 edge라고 부르죠. 그리고 root 부터 특정 leaf까지 가는 길을 path라고 합니다. 위의 그림에서 root 부터 j까지 가는 path는 높이 3을 가지겠죠. 3단계의 branch를 거쳤으니까요. 이렇게 부모와 자식 노드 사이의 branch 갯수를 height라고 합니다.
트리 구조의 용도
트리 구조는 일상 생활에서도 많이 쓰입니다. 군대를 다녀온 남자분들은 아실텐데요. 군대에서의 계급체계 또한 트리 구조로 되어있죠. (확 체감이 되네요...) 실제 컴퓨터에서 리눅스, 윈도우 파일시스템 또한 트리 구조로 되어있습니다. 트리 구조를 활용하면 엄청난 양의 데이터를 저장하는 데 용이합니다.
트리의 시간복잡도
javascript 트리 구현
구현에서 중요한 점은 자식의 주소를 어떻게 부모 노드에 저장할 것인지 입니다. 배열에 자식 노드들의 주소를 담으면 되죠. 자식 노드를 생성하고 배열을 사용해 부모 노드에 담으면 자바스크립트가 알아서 자식노드의 주소를 매핑해줍니다.
class Node {
constructor(data) {
this.data = data;
this.children = []; // 자식 노드들이 담길 배열입니다.
}
add(data) {
// 자식 노드를 추가하는 메서드입니다. 시간복잡도 O(1)이겠죠.
this.children.push(new Node(data));
}
remove(data) {
// 자식 노드를 삭제하는 메서드입니다.최악의 경우 시간복잡도 O(N)입니다.
this.children = this.children.filter((child) => child.data !== data);
}
}
class Tree {
constructor() {
this.root = null;
}
}
const tree = new Tree();
tree.root = new Node("루트 노드입니다.");
tree.root.add("자식1");
tree.root.add("자식2");
tree.root.add("자식3");
tree.root.add("자식4");
console.log(tree);
//
Tree {
root: Node {
data: '루트 노드입니다.',
children: [ [Node], [Node], [Node], [Node] ]
}
}BFS(Breadth Frist Search) 너비우선탐색
BFS(너비우선탐색)은 root 노드부터 시작해서 가장 가까운 노드를 먼저 탐색합니다. 장점으로 최단거리를 찾을 때 주로 사용하죠. 예를 들어 구글 맵에서 특정 위치까지의 최단거리를 안내하거나, 페이스북에서 친구 추천을 할 때 BFS를 활용합니다. 반면, BFS는 큐를 활용해 노드를 담았다 뺐다 하기 때문에 메모리를 많이 잡아먹는다는 단점이 있습니다.
우리가 아직 방문하지 않은 노드들이 생성한 큐에 담기기 때문에 만약 큐에 노드가 있으면 탐색이 끝나지 않은 것입니다. 따라서 우리는 큐의 길이가 0이 될 때까지 반복문을 돌리면 되겠죠?
구현
class Tree {
constructor() {
this.root = null;
}
BFS(callback) {
if (this.root === null) return;
const queue = [this.root];
while (queue.length !== 0) {
const currentNode = queue.shift();
queue.push(...currentNode.children);
let bool = callback(currentNode);
if (bool) {
console.log("일치", currentNode);
} else {
console.log("불일치");
}
}
}
}
function findNodeCallback(node) {
if (node.data === "2-3") {
return true;
}
return false;
}
const tree = new Tree();
tree.root = new Node("루트 노드입니다.");
tree.root.add("자식1");
tree.root.children[0].add("1-1");
tree.root.add("자식2");
tree.root.children[1].add("2-1");
tree.root.children[1].add("2-2");
tree.root.children[1].add("2-3");
tree.root.add("자식3");
tree.root.children[2].add("3-1");
tree.root.children[2].add("3-2");
tree.root.add("자식4");
tree.root.children[3].add("4-1");
tree.BFS(findNodeCallback);
//
불일치
불일치
불일치
불일치
불일치
불일치
불일치
불일치
일치 Node { data: '2-3', children: [] }
불일치
불일치
불일치여기 이해하는 키 포인트는 queue에 탐색할 요소들이 push() 메서드로 뒤에 쌓이는 것입니다. 너비탐색의 순서대로 쌓이기 때문에 BFS를 탐색 방법을 유지할 수 있죠. 그러다가 queue가 빈 배열이 되게 되면 끝나겠죠.
위의 코드에서는 '2-3'의 데이터를 가지는 노드를 찾는 콜백함수를 인자로 넘겨줬습니다. 따라서 노드를 찾았을 때 콘솔 창에 노드를 출력한 것을 볼 수 있죠.
DFS(Depth First Search) 깊이우선탐색
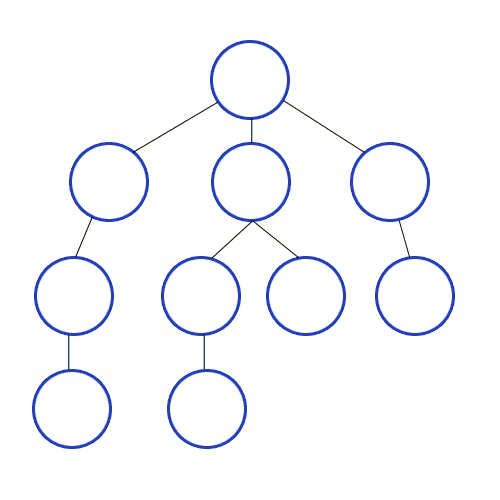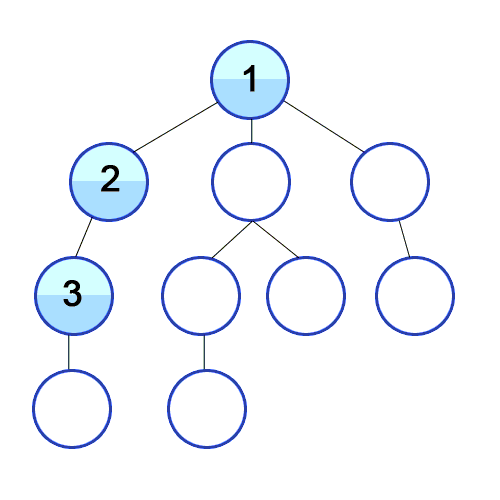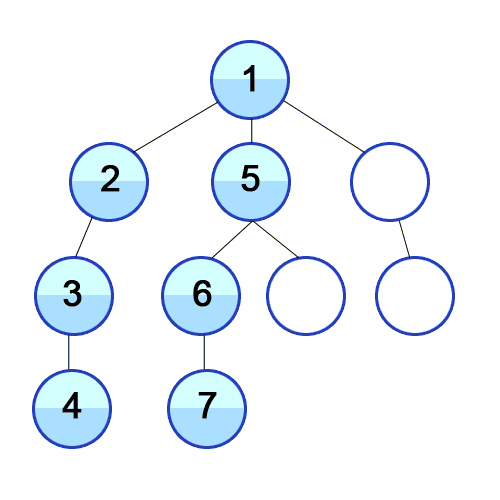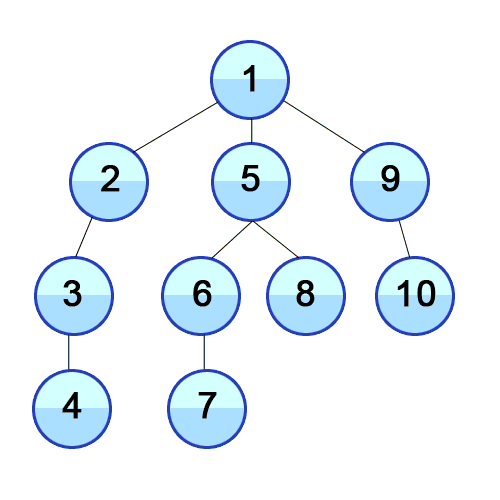
BFS의 개념을 이해했다면 DFS는 금방 이해할 것 입니다. BFS 구현에서 우리는 부모 노드와 가장 가까운 자식 노드를 먼저 다 찾고나서 그 다음 depth로 넘어갔죠? DFS는 한 자식만 주구장창 파고 내려갑니다. 그러다 더는 내려갈 깊이가 없으면 옆에 있는 자식을 같은 방식으로 탐색하죠.
구현
BFS는 queue에서 노드를 추가할 때 push() 메서드로 뒤에다 추가해줬었죠. DFS를 구현할 때는 unshift() 메서드로 앞에다 추가해주면 됩니다.
class Tree {
constructor() {
this.root = null;
}
DFS(callback) {
if (this.root === null) return;
const queue = [this.root];
while (queue.length !== 0) {
const currentNode = queue.shift();
queue.unshift(...currentNode.children);
let bool = callback(currentNode);
if (bool) {
console.log("일치", currentNode);
} else {
console.log("불일치");
}
}
}
}
function findNodeCallback(node) {
if (node.data === "2-3") {
return true;
}
return false;
}
const tree = new Tree();
tree.root = new Node("루트 노드입니다.");
tree.root.add("자식1");
tree.root.children[0].add("1-1");
tree.root.add("자식2");
tree.root.children[1].add("2-1");
tree.root.children[1].add("2-2");
tree.root.children[1].add("2-3");
tree.root.add("자식3");
tree.root.children[2].add("3-1");
tree.root.children[2].add("3-2");
tree.root.add("자식4");
tree.root.children[3].add("4-1");
tree.DFS(findNodeCallback);
//
불일치
불일치
불일치
불일치
불일치
불일치
일치 Node { data: '2-3', children: [] }
불일치
불일치
불일치
불일치
불일치마치며
본격적으로 자료구조, 알고리즘을 시작했는데 용어만 들었고 정확히 무엇인지 몰랐던 트리, BFS, DFS를 한 번 정리하고 나니까 조금은 마음이 차올랐다.(?) 실무 능력도 중요하겠지만 알게 모르게 차이를 만드는 개발자의 기본 지식이라고 할 수 있는 알고리즘, 자료구조 열심히 공부해서 좋은 회사에 들어가고 싶다!
