개념

---

이진탐색트리 설명에 앞서 이진트리를 설명해보겠습니다. 여러개의 자식을 가질 수 있는 트리와는 다르게 이진트리는 최대 2개의 자식만을 가질 수 있는 트리입니다.

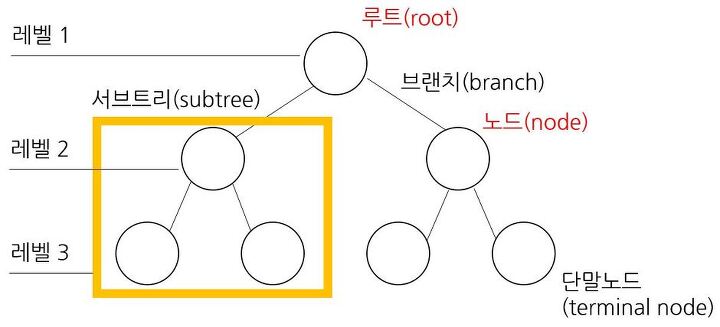
그럼 이진탐색트리는 뭘까요? 이진탐색트리는 이진트리에서 2개의 규칙을 적용한 트리를 말합니다. 2개의 규칙은 아래와 같습니다.

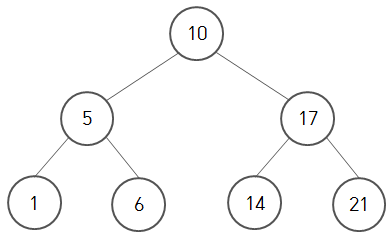
• 왼쪽 자식 노드는 부모 노드보다 값이 작다.
• 오른쪽 자식 노드는 부모 노드보다 값이 크다.

따라서 이를 구현하면 다음과 같은 그림의 트리 구조를 얻게 됩니다.

시간복잡도

---

이진검색트리의 시간복잡도는 $logN$입니다. 왜 그런지 알아보죠. 이진검색트리의 노드의 갯수를 N개라고 가정해봅시다. 만약 브랜치 하나를 내려오게 되면 반대쪽 서브트리들은 검색 대상에서 제외됩니다. 즉,

• 처음 검색 시행 후 노드의 갯수는 $\frac{N}{2}$
• 두번째 검색 시행 후 노드의 갯수는 $\frac{1}{2}*\frac{N}{2}$
• k번 검색 시행 후 노드의 갯수는 $(\frac{1}{2})^k * N$

이렇게 반복해서 검색을 시행하다가 최악의 경우 탐색이 끝나는 시점에서 남은 노드는 1개가 남을 것입니다.

$(\frac{1}{2})^kN = 1$

이라고 할 수 있겠죠. 양변에 $2^k$를 곱하면

$N = 2^K$

가 되고 양변에 $log_2$를 취하게 되면 결과적으로 다음과 같은 결과를 얻게됩니다.

$log_2N = K$

즉, $K$는 시행횟수이고 시간복잡도는 상수부분을 무시하기 때문에 이진탐색트리의 시간복잡도는 $`logN`$이 됩니다.

구현

---

이진탐색트리 구현의 핵심은 노드 메소드에 left, right를 만들어 각각이 자식 노드의 주소를 가르키도록 하는 것입니다. 시나리오를 써보죠.

1. insert 메소드를 호출해 data를 넘겨주면 data가 부모의 data보다 큰 지 작은 지 판별합니다.
2. 만약 작다면 부모의 left를 호출하고 크다면 right를 호출합니다.
3. 그 자리에 이미 노드가 있는지 없는지를 판별합니다.
4. 만약 있다면 그 자식 노드의 insert를 호출합니다. this.left.insert(data), 없다면 this.left = new Node(data)로 노드를 삽입해주면 되겠죠. 여기서 left가 right가 될 수도 있겠죠?

4번에서 만약 자식 노드가 이미 있다면 그 노드의 insert 메서드를 다시 호출했죠. 여기서 재귀함수의 개념이 사용됩니다. 이를 염두해서 구현을 하시면 쉽게 할 수 있을겁니다.

직접 만들어보느라 깔끔한 코드는 아니지만 삽입과 검색 메서드를 구현했습니다.

class Node {
    constructor(data) {
        this.data = data;
        this.left = null;
        this.right = null;
    }
}

class BinarySearchTree {
    constructor(data) {
        this.root = new Node(data);
        this.current = this.root;
    }

    // 삽입
    insert(data) {
        if (data < this.current.data) {
            if (this.current.left) {
                this.current = this.current.left;
                this.insert(data);
            } else {
                this.current.left = new Node(data);
                this.current = this.root;
            }
        } else if (data > this.current.data) {
            if (this.current.right) {
                this.current = this.current.right;
                this.insert(data);
            } else {
                this.current.right = new Node(data);
                this.current = this.root;
            }
        } else {
            console.log("노드가 이미 존재합니다.", data);
            this.current = this.root;
        }
    }
		
    // 검색
    search(data) {
        if (data === this.current.data) {
            console.log("데이터 찾았습니다.", this.current);
            this.current = this.root;
            return;
        }

        if (data < this.current.data) {
            if (this.current.left) {
                this.current = this.current.left;
                this.search(data);
            } else {
                console.log("없는 데이터입니다.");
                this.current = this.root;
                return;
            }
            this.current = this.current.left;
        } else {
            if (this.current.right) {
                this.current = this.current.right;
                this.search(data);
            } else {
                console.log("없는 데이터입니다.");
                this.current = this.root;
                return;
            }
        }
    }
}