perception은 주행 환경을 인지하는 과정으로 유의미한 정보를 생성하는 단계가 필요하다. 영상 데이터의 경우 이미지 영역에서 객체를 인식하는 것이 아닌 객체와 차량의 관계를 파악하는 것이 중요하다.
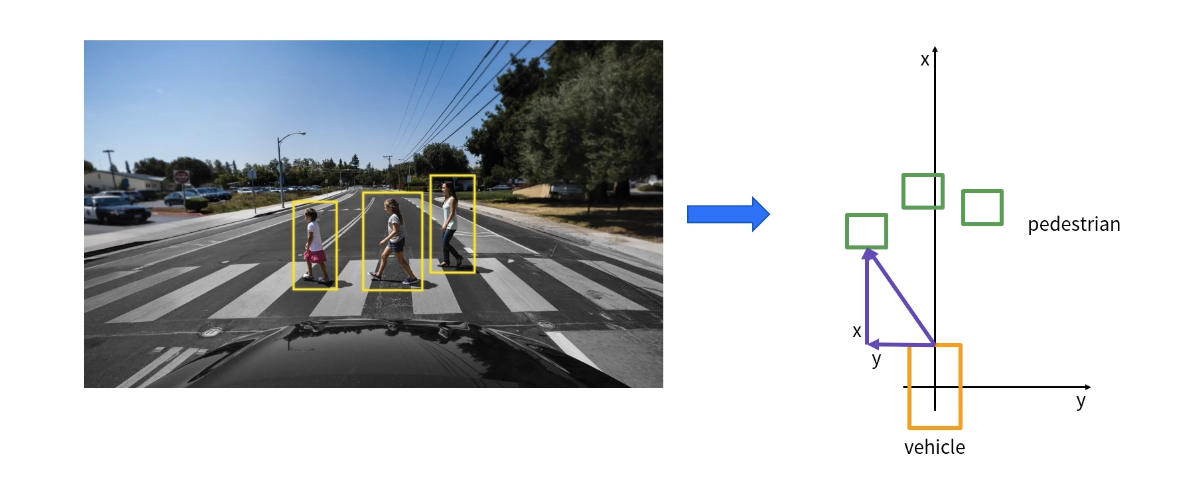
위와 같이 영상에 존재하는 객체의 위치를 카메라로부터 어디에 위치하고, 어떤 방향을 보고 있는지를 예측하는 기술이 필요하며 이를 3D POSE(Position and Orientation) estimation 이라고 한다. 이를 위해서는 기하학적인 지식을 필요로 한다.
Camera model
카메라는 3차원 공간인 실세계를 2차원 평면인 이미지 공간으로 투영하는 센서이다. (빛을 감지하는 센서) camera model은 카메라의 투영 과정을 수학 모델로 표현한 것이다.
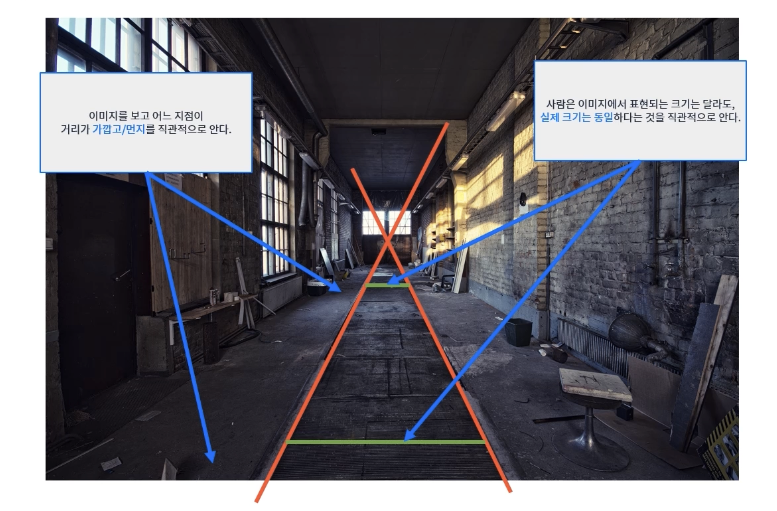
사람은 이미지 한장을 봐도 원근을 이해할 수 있지만 카메라는 그렇지 못한다. 하지만 영상의 경우 하나의 구멍으로 들어온 빛을통해 영상을 기록하기 때문에 특정 영역으로 모여 들어가는 형태로 나타나며 이를 소실점이라 한다.
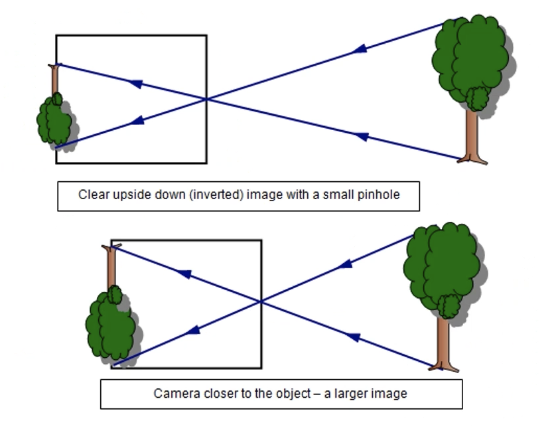
빛은 직선으로 들어온다. 카메라와 물체의 거리가 멀어질수록 객체의 크기는 작아진다.
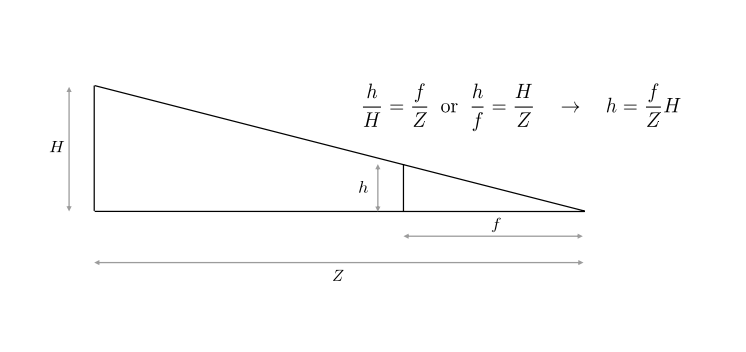
카메라는 위와 같이 실세계의 물체와 이미지 공간에 표현되는 물체간의 관계를 정의할 수 있다.
Intrinsic calibration
Intrinsic은 카메라가 가지고 있는 고유한 특성을 의미한다. 여기에는 렌즈와 이미지 센서 사이의 거리(초점 거리)와 굴곡 등이 포함된다. Intrinsic calibration은 intrinsic 값을 구하는 과정을 의마한다. 다시 말해 카메라가 가지고 있는 고유한 특성을 파악하는 과정이라고 볼 수 있다.
초점거리가 클수록, 믈체와의 거리가 가까울수록 피사체를 크게 촬영된다.

Intrinsic에는 초점거리(fx, fy)와 주점(cy, cx)이 포함된다. 초점거리는
이상적인 카메라의 경우 fx와 fy가 유사하다.
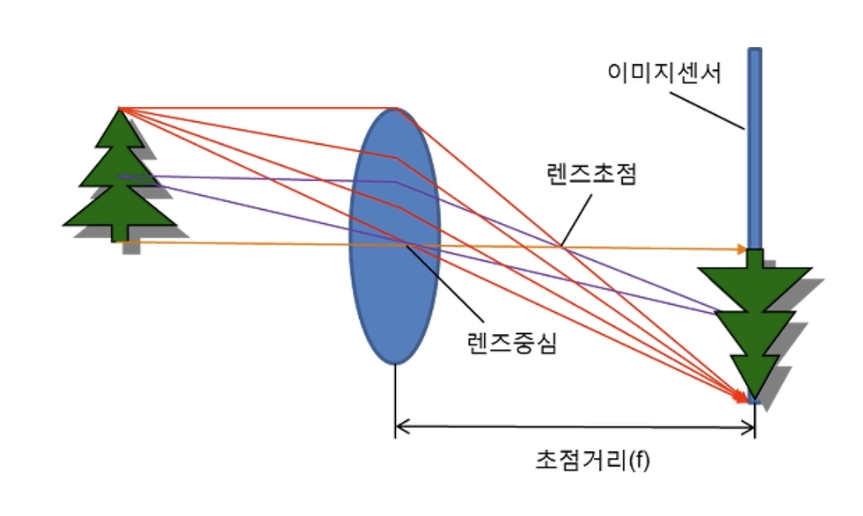
상이 맺히는 이미지 센서와 렌즈와의 거리를 초점거리(Focal length)라고 하는데 초점거리가 너무 가깝거나 멀면 상이 흐려진다. 우리가 카메라나 빔프로젝터를 사용할 때 앞에있는 렌즈를 돌려 초점을 맞추는 원리가 이 경우에 해당한다.
핀홀(Pinhole)은 렌즈, 상이 맺히는 벽은 이미지 센서이다.
초점 거리의 물지적인 단위
카메라에서는 이미지 센서(CCD or CMOS)와 렌즈의 중심 거리 사이의 거리는 실제 물리 단위인 mm로 표현한다. 특히 Computer vision에서는 이미지 센서의 Cell 크기에 대한 상대적인 pixel로 표현한다.
초점거리 pixel을 mm로 변환하는 방법은 다음과 같다. 만약 이미지 센서의 한 cell의 크기가 0.1mm 이고, 초점거리가 500pixel이라고 한다면, 이미지 센서와 렌즈 중심과의 거리는 가 된다.
또한 이미지 센서의 크기는 변하지 않기 때문에 해상도에 따라 초점거리가 달리는 것을 설명할 수 있다.
예를 들어, 한 cell의 크기가 0.1mm인 100x100 크기의 이미지 센서가 있고, 이 센서로 100x100 해상도를 갖는 이미지를 표현한다면 이미지의 한 픽셀은 하나의 이미지 센서로 표현된 것이라고 할 수 있다. 만약 이미지의 해상도를 절반으로 줄인다고 하면, 이미지의 한 픽셀은 이미지 센서의 4개의 cell로 표현될 것이다. 이때 초점거리가 50mm라고 한다면, 을 으로 초점거리가 절반으로 줄어든 것을 확인할 수 있다. 즉, 초점거리를 줄이면 이미지 해상도가 줄어든다는 것을 설명할 수 있다.
주점(Principal point)은?
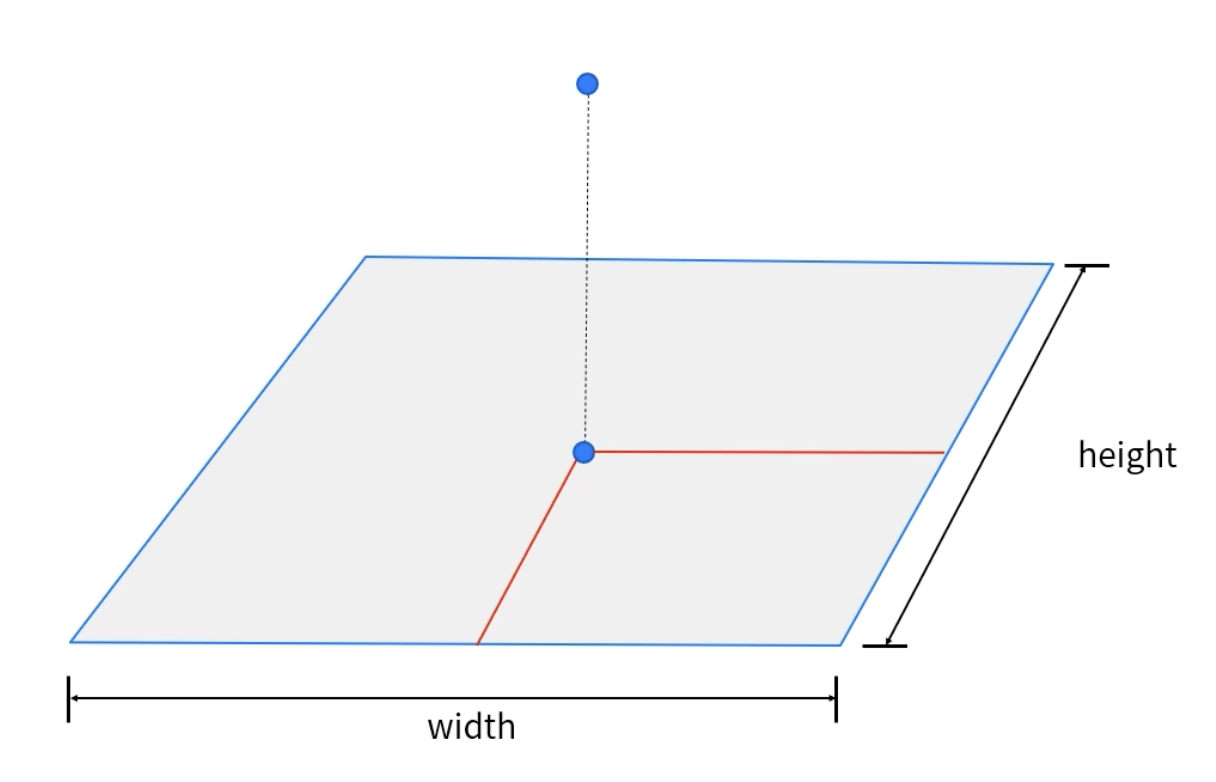
주점은 렌즈의 중심으로부터 내려온 수직선이 이미지 센서에 만나는 지정을 의미한다. 주점은 이미지의 중심점과 다를 수 있다.(제조 과정에의 문제) 때문에 주점의 위치를 알기 위해서는 calibration 과정이 수행되어야 한다.
Intrinsic calibration 이란?
Intrinsic calibration은 Intrinsic parameter를 파악하는 과정이다.
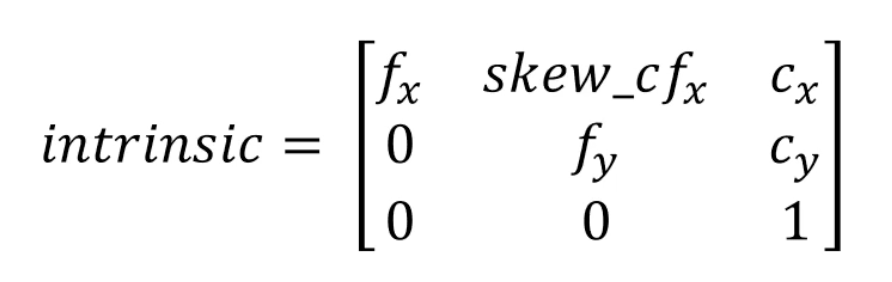
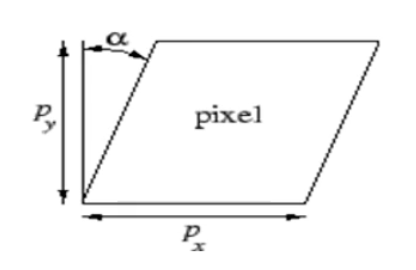
skew는 이미지 센서가 y축 방향으로 기울어진 정도를 나타내는 척도로 요즘에는 잘 사용되지 않는다.
Intrinsic calibraion이 필요한 이유
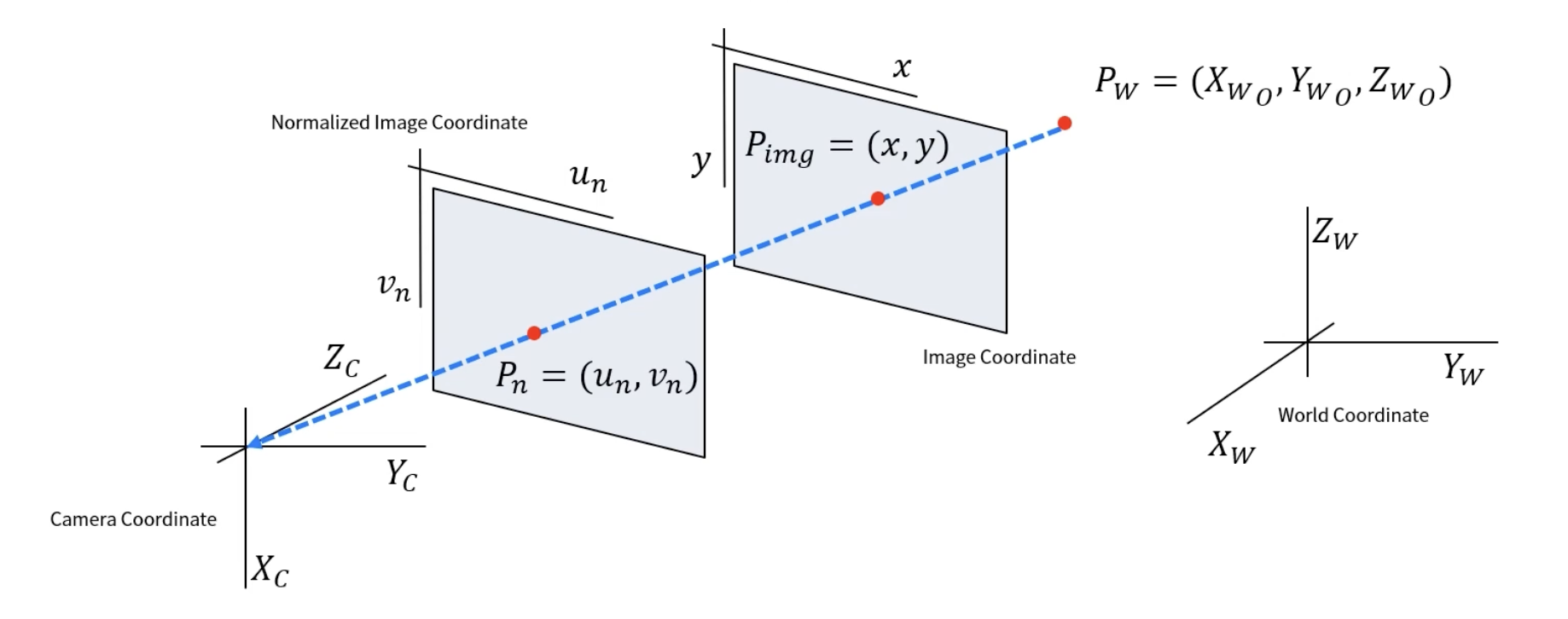
정규 이미지 좌표계는 카메라 좌표계에서 1만큼 떨어져 있는 가상의 좌표계로 서 로다른 카메라에서 영상 처리를 위해 통일화 시키기 위해 만든 좌표계이다.
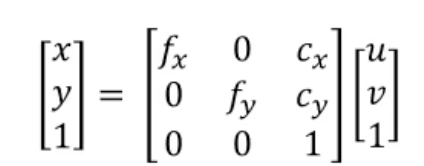
카메라의 Intrinsic calibration 정보를 알면 이미지 좌표계에서 정규 이미지 좌표계로 혹은 정규 이미지 좌표계를 이미지 좌표계로 변환이 가능하다.
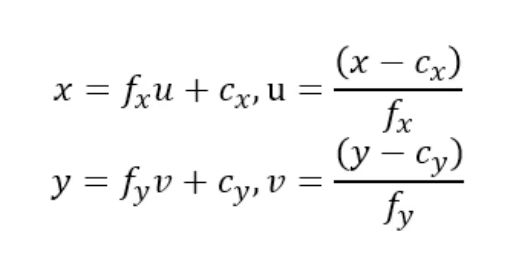
위 행렬식을 풀어 u와 v에 대한 값을 구할 수 있다. 또한 이를 통해 만든 정규 이미지 좌표계는 다른 카메라의 intrinsic 정보를 알면 해당 카메라의 이미지 공간으로 이동시킬 수 있다.
Distortion(왜곡)

빛의 굴절에 의해 이미지가 왜곡되는 현상을 의미한다. 렌즈를 통과하는 과정에서 빛이 굴절되거나 산란되기 때문에 이미지 센서에 상이 한 점으로 모이지 않아 이미지에 왜곡이 발생할 수 있다.
왜곡은 왜 발생하는가?
- 렌즈에 특성에 의해서 발생한다.
- 렌즈와 이미지 센서 간의 관계에 의해서 발생한다.
렌즈의 곡률에 의한 왜곡
왜곡은 렌즈의 형상이 곡률을 갖는 구면 형태이기 때문에 발생한다. 때문에 이미지의 중심(주점)으로부터 멀어질수록 비율이 달라진다 이는 아래 그림과 같으며, 오른쪽의 수식으로 표현이 가능하다.
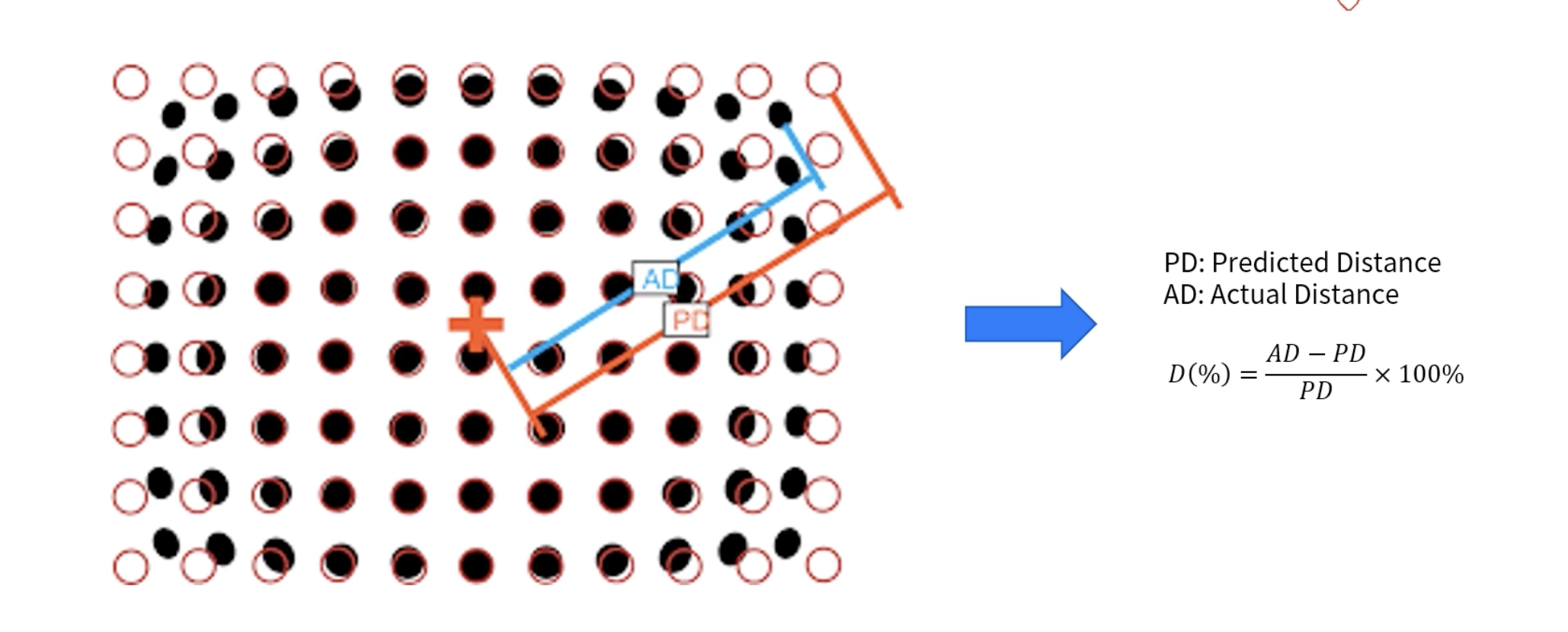
왜곡의 종류
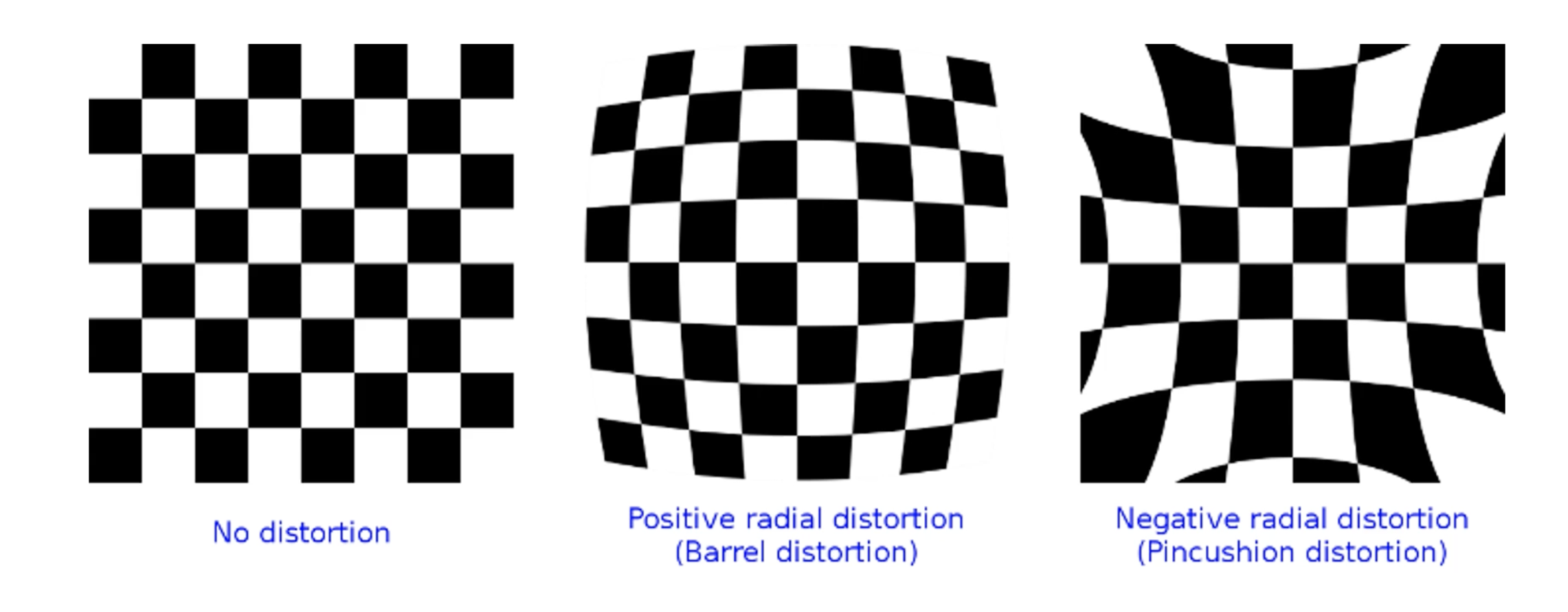
- 방사 왜곡이 대표적인 형태로 두 형태로 나타난다.
Barrel distortion: 중심부로 갈수록 왜곡이 심해지는 형태
Pincushion distortion: 외각으로 가수록 왜곡이 심해지는 형태
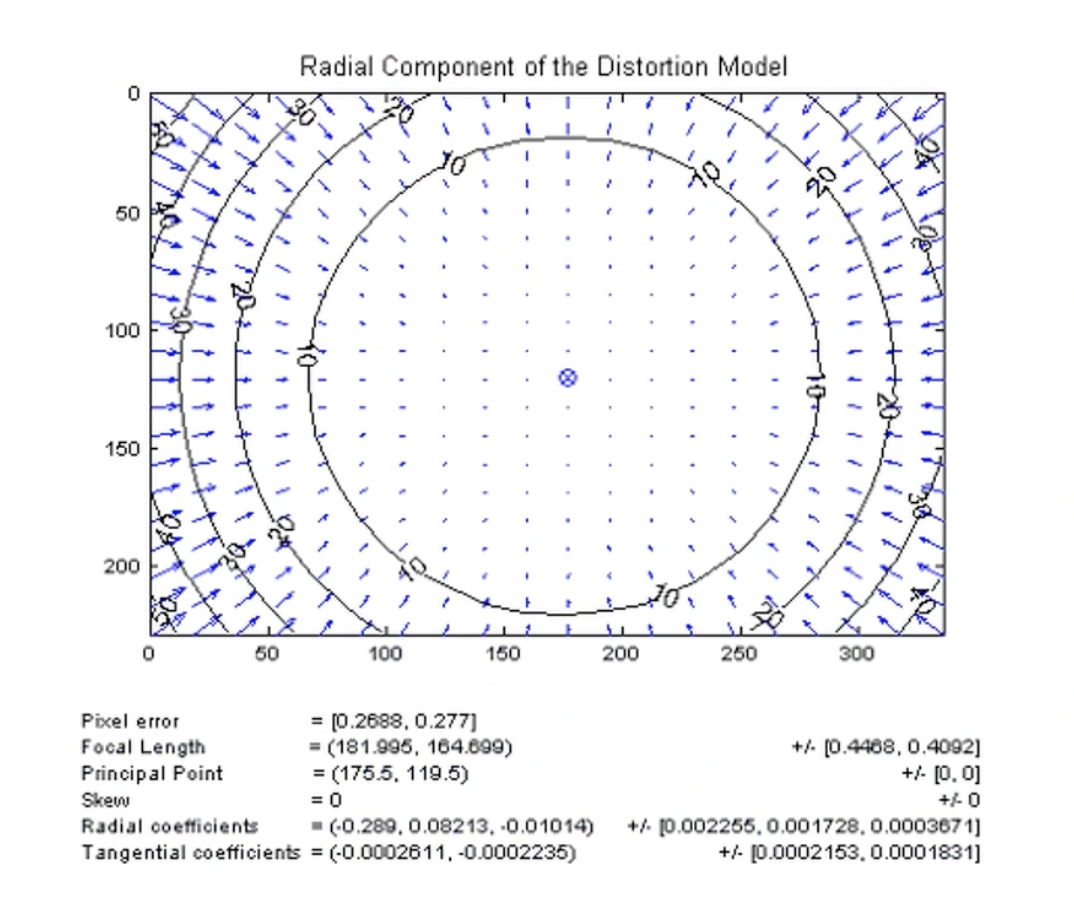
- 접선 왜곡(Tangential distortion)
접선 왜곡은 렌즈와 이미지 센서간의 수평이 맞지 않은 경우에 발생한다.
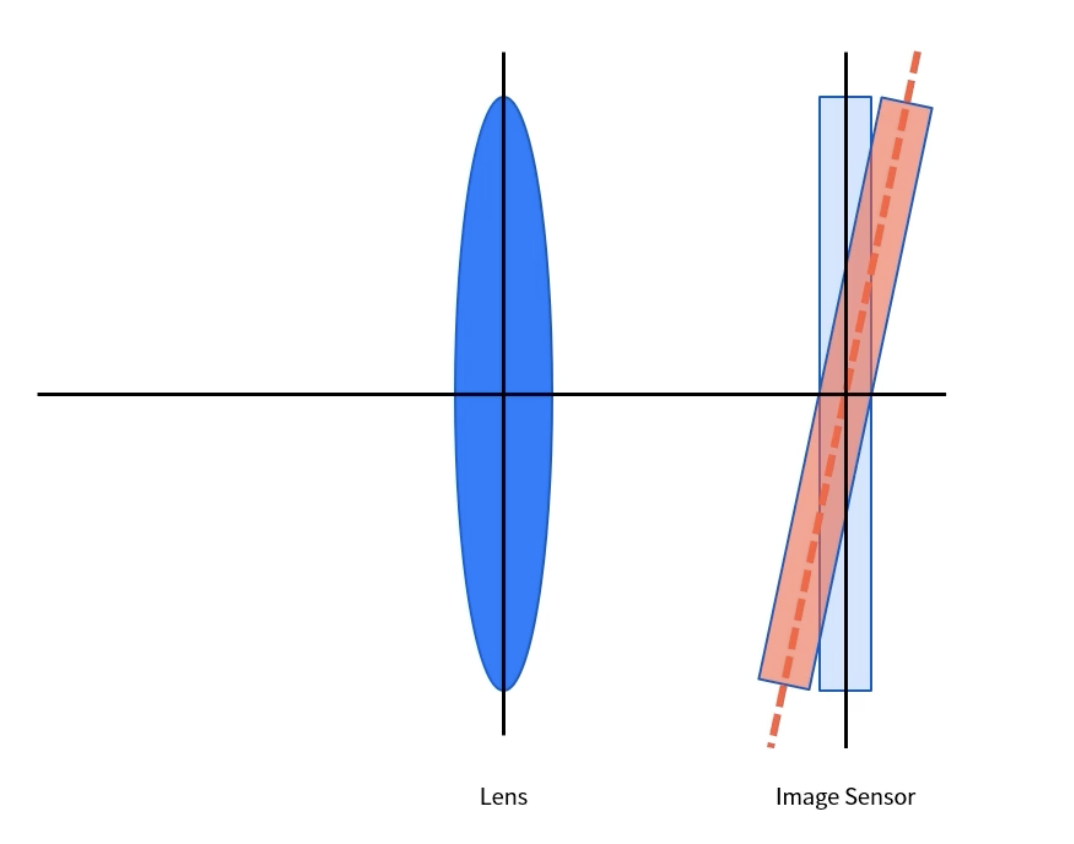
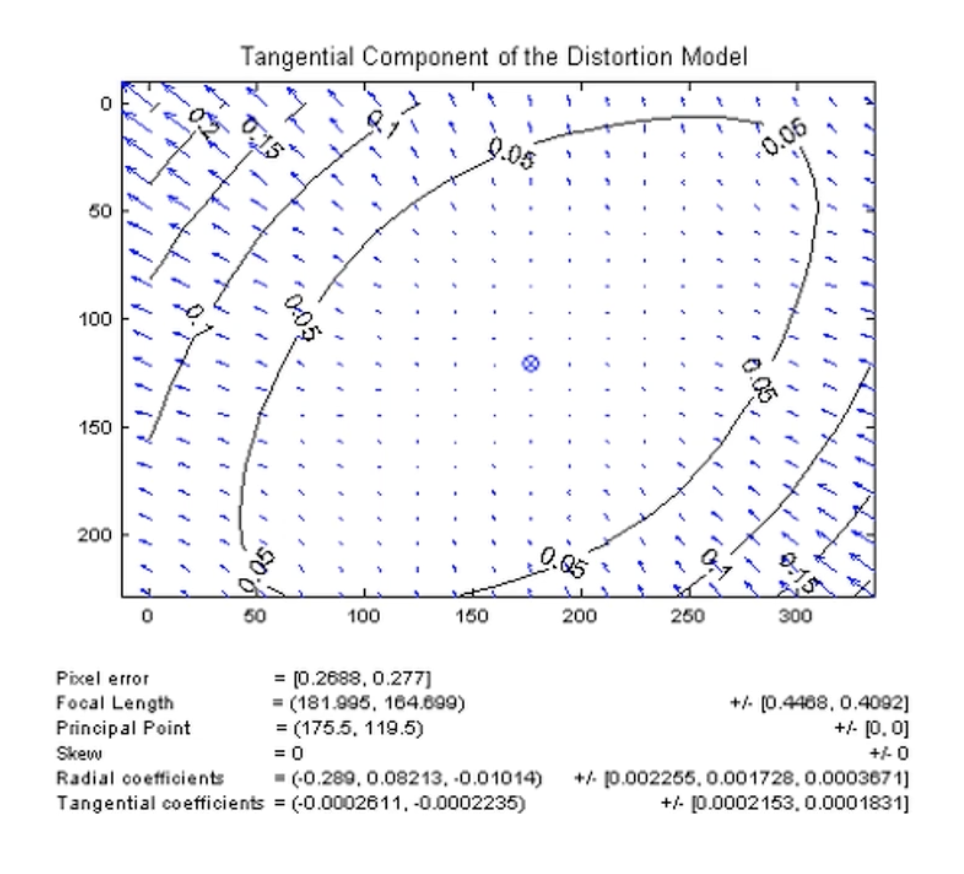
- 원근 왜곡(Perspective distortion)
3차원 공간이 2차원 공간으로 투영되면서 발생하는 왜곡이다. 이미지는 깊이 정보를 하나의 평면으로 투영하는 데이터이기 때문에 다음과 같은 원근 왜곡이 나타날 수 있다.

원근 왜곡의 경우 위 두 왜곡과 달리 한장의 이미지로는 원근 왜곡을 보정할 수 없다. 하지만 다수의 이미지 혹은 카메라를 이용해서 보정할 수 있다.
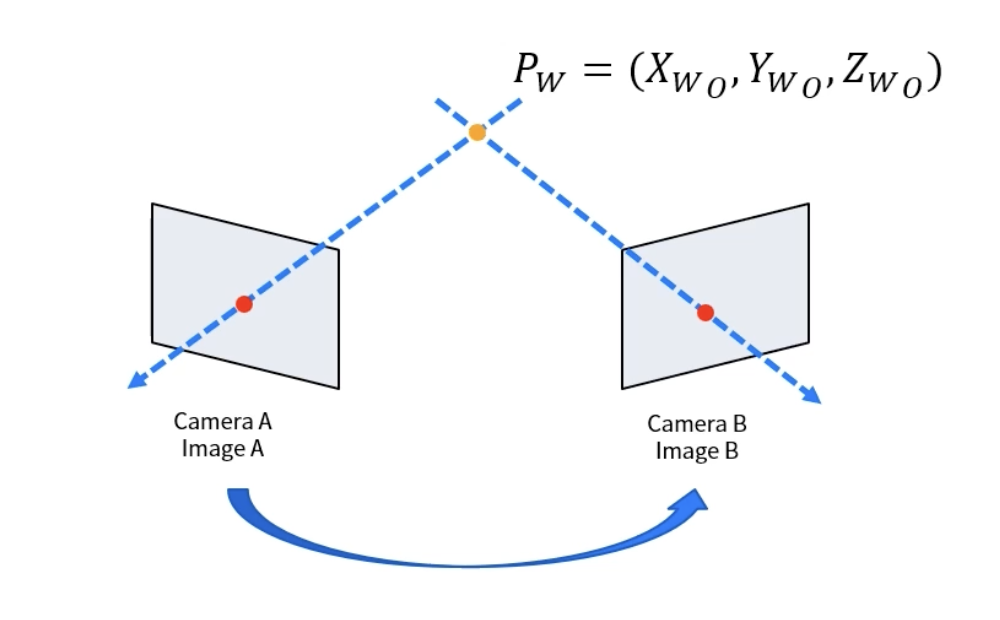
- 두 개의 카메라를 이용하는 방법
* 각 카메라의 Extrinsic parameter를 알아야 정확한 정보를 추정할 수 있다. - 두 장 이상의 이미지를 이용하는 방법
* 동일한 카메라를 통해 움직이는 과정에서 얻은 이미지 정보를 활용하여 3차원 위치 정보를 추정할 수 있다. 다만 카메라의 움직임 정보를 정밀하게 측정 및 추정해야 한다.
이미지 왜곡은 왜 문제가 되나?
이미지의 기하학적 정보를 해석하는데 방해되기 때문이다.

왜곡 모델링
왜곡이 없는 경우
3차원 공간의 물체를 2차원 이미지 공간에 투영하기 위해서는 위와 같이 Extrinsic과 Intrinsic 행렬을 통해 변환된다.
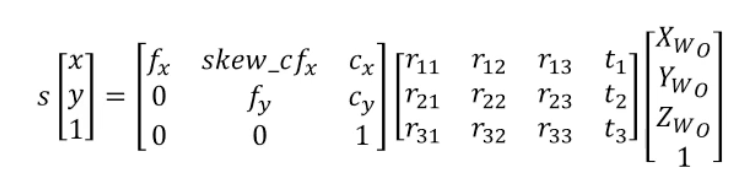
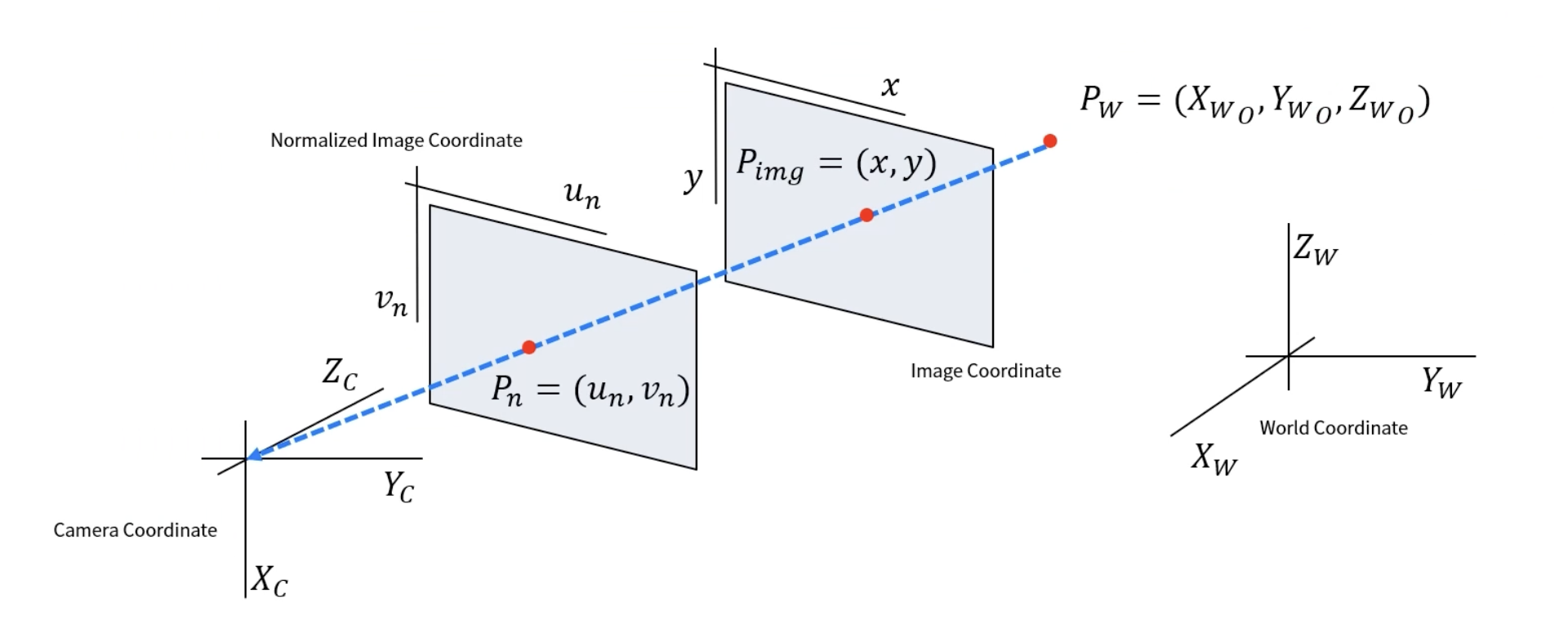
왜곡을 모델링하기 위해서 카메라 좌표계를 기준으로 설명한다. 먼저 3차원의 물체를 2차원 공간으로 투영한다고 했을 때,
카메라 모델은 위와 같다. 먼저 Extrinsic은 회전과 이동에 관한 정보를 가지고있는 3x4 크기의 행렬로 구성된다. 하지만 현재 단계에서는 카메라의 회전과 이동이 왜곡에 영향을 미치지 않는다고 가정한다. 또한 정규 이미지 공간에 이미지를 투영하는 경우에는 Intrinsic 정보 또한 필요가 없다.
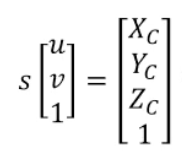
즉, 3차원에 물체를 2차원으로 투영하는 과정을 위와 같이 정리할 수 있다.
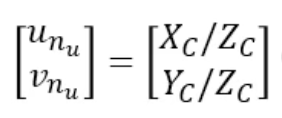
마지막으로 위와 같이 벡터의 마지막 요소로 나눠주면, 왜곡이 없는 상태에서의 3차원의 2차원 변환 과정이 끝난다.
왜곡이 있는 경우
방사 왜곡와 접선 왜곡은 다음의 두 형태로 모델이 가능하다. 왜곡 모델은 정규 이미지 공간에서 정의된다. 왜곡을 제거하는 방법은 왜곡 이미지를 왜곡이 없는 이미지로 mapping하는 것을 의미한다.
다음은 왜곡이 없는 이미지를 왜곡된 이미지로 만드는 과정이다.
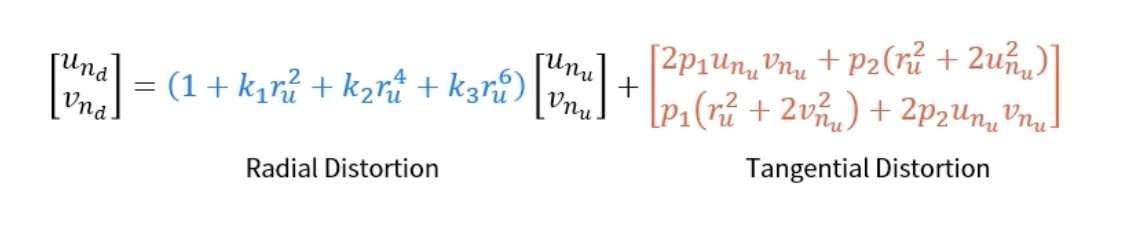
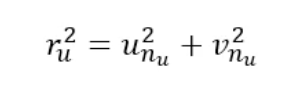
r은 주점으로 부터 특정 픽셀이 떨어진 거리를 의미한다.
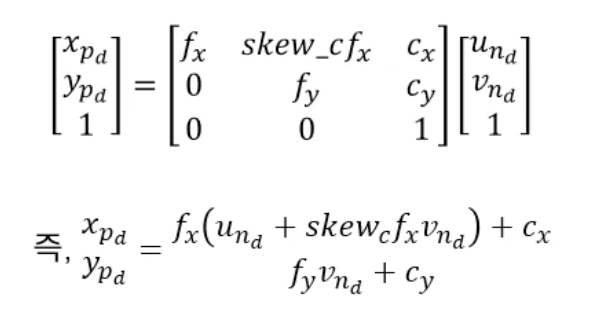
반대로 왜곡이 있는 이미지를 왜곡이 없는 이미지로 만드는 방법이다.

