[VSLAM 5] Camera projection

Camera obscura

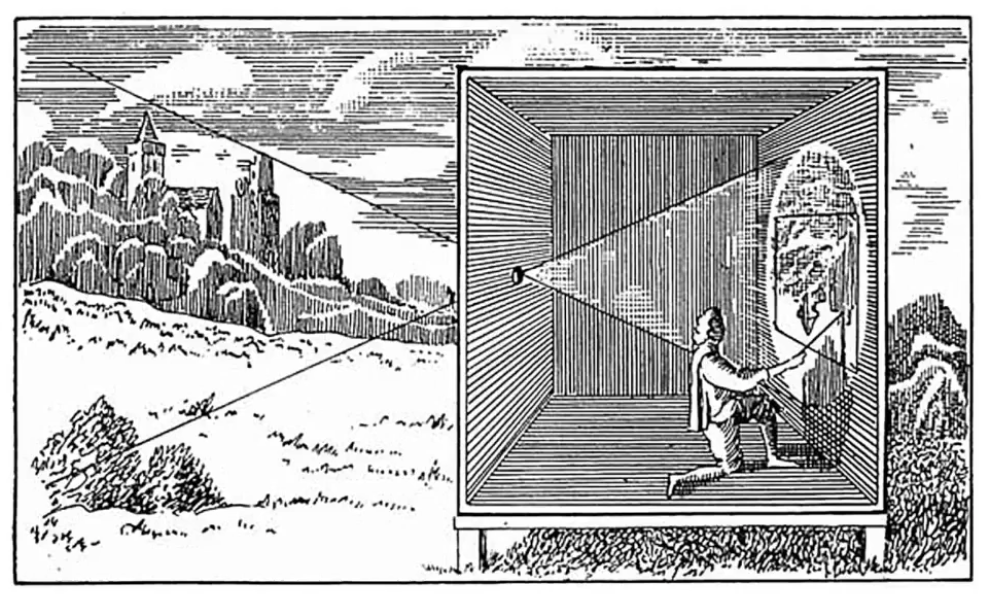
바늘 구멍 사진기의 원리는 암실로된 상자에 작은 구멍으로 들어온 빛이 상자 반대에 상으로 맺히는 것을 기본적인 원리로 한다. 이를 통해 투영과 같은 수학적인 원리를 만드는데 많은 기여를 했다.

원리1. 빛은 직선으로 이동한다. 상이 거꾸로 맺히는 것이 바로 이 원리에 의한 것이다.
원리2. 상 맺힘이다. 3D 공간이 2D 이미지 즉 하나의 상으로 투영된다는 것이다.

현대의 카메라도 이러한 원리를 그대로 계승한다.

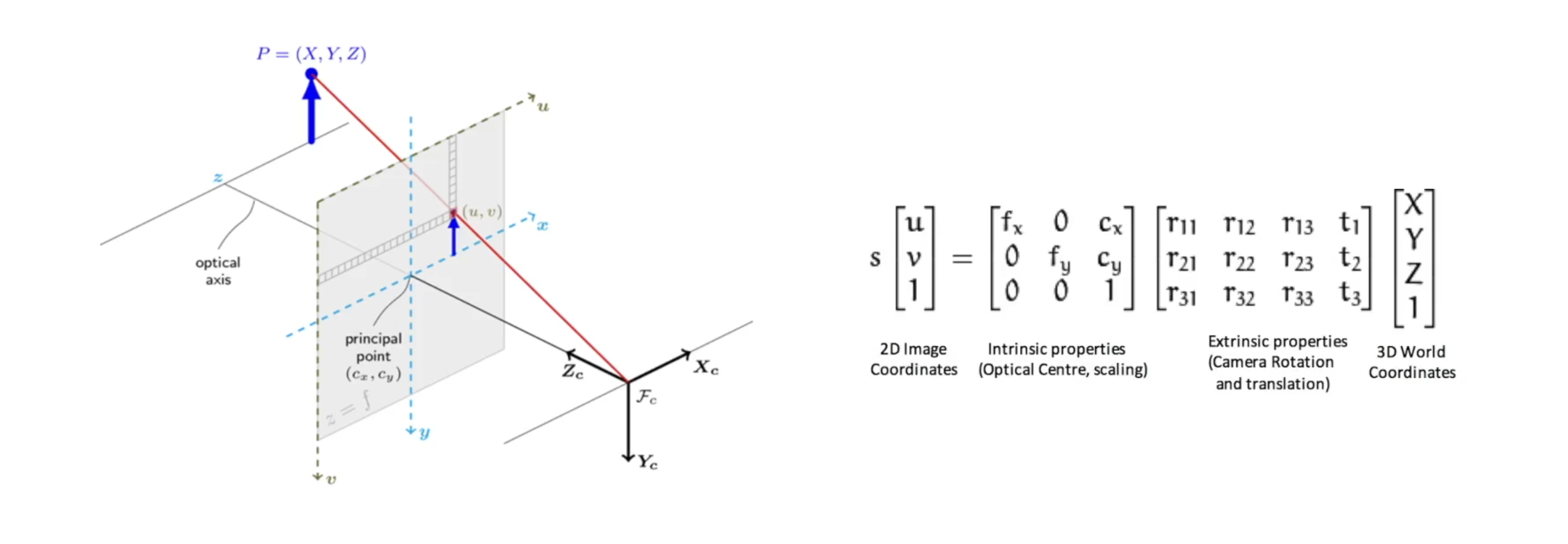
Camera projection

3D 좌표계를 2D 좌표계로 맵핑하는 과정이다.

카메라 투영은 위 식으로 표현이 가능하다. x는 2d 공간의 좌표계, P는 3d to 2d 투영을 위한 matrix 그리고 X는 3d 좌표계를 의미한다.

또한 projection은 world coordinate system(3D)을 camera coordinate system으로 바꾸고 이를 다시 image coordinate system(2D)로 바꾸는 과정을 통해 이루어진다.

World coordinate to camera coordinate transformation

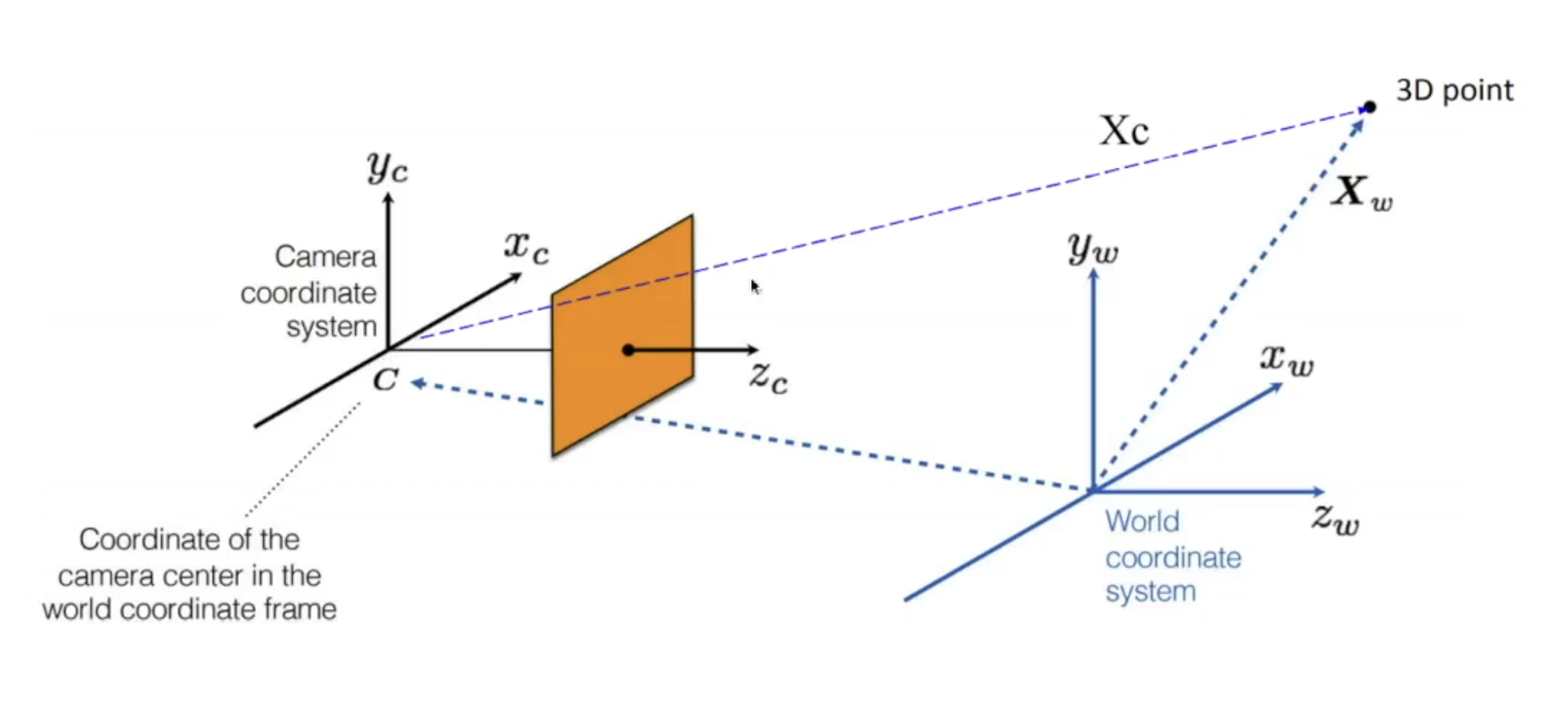
3d 좌표계를 camera 좌표계로 바꾸는 과정이다. 이 과정에서 3d 상의 한 객체는 회전과 이동 변환을 통해 camera 좌표계의 이동을 변환이 가능하다.

3d world 정보를 camera coordinate로 변환함으로써 3d world에 관한 계산을 고려하지 않을 수 있다. (world frame 제거)

Camera coordinate to image coordinate transformation

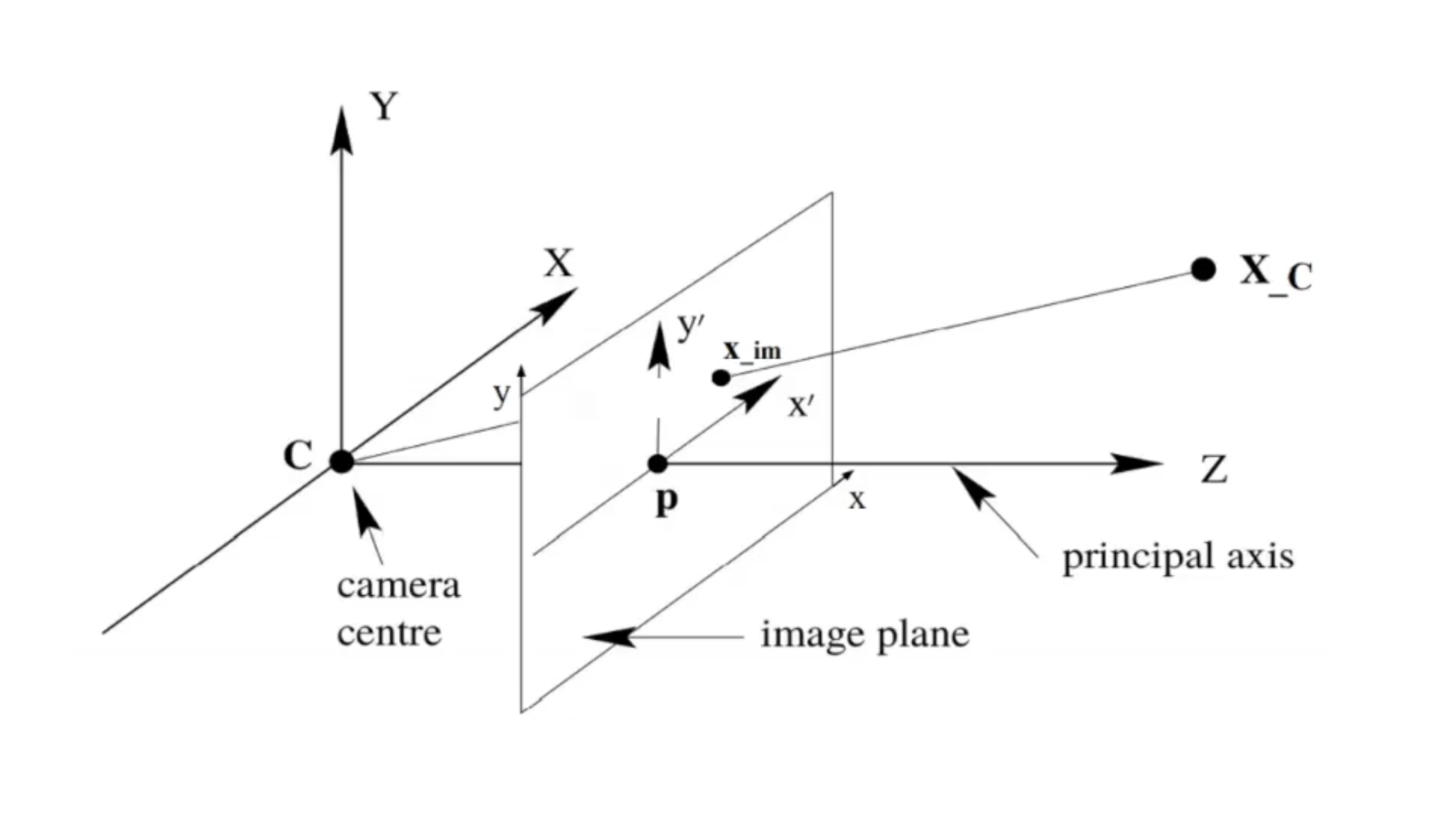
위 과정을 통해 world coordinate가 제거되어 $X_c$와 camera coordinate만 남게된다. 이때 world coordinate의 한 점인 $X_c$과 camera coordinate의 원점을 지나는 직선을 그리게 되면 Image plane의 한 곳을 지나는 점을 얻을 수 있다. camera projection은 world coordinate의 $X_c$를 image plane 상의 한 점으로 바꾸는 역할을 하는 수식을 찾는 과정이라고 할 수 있다.

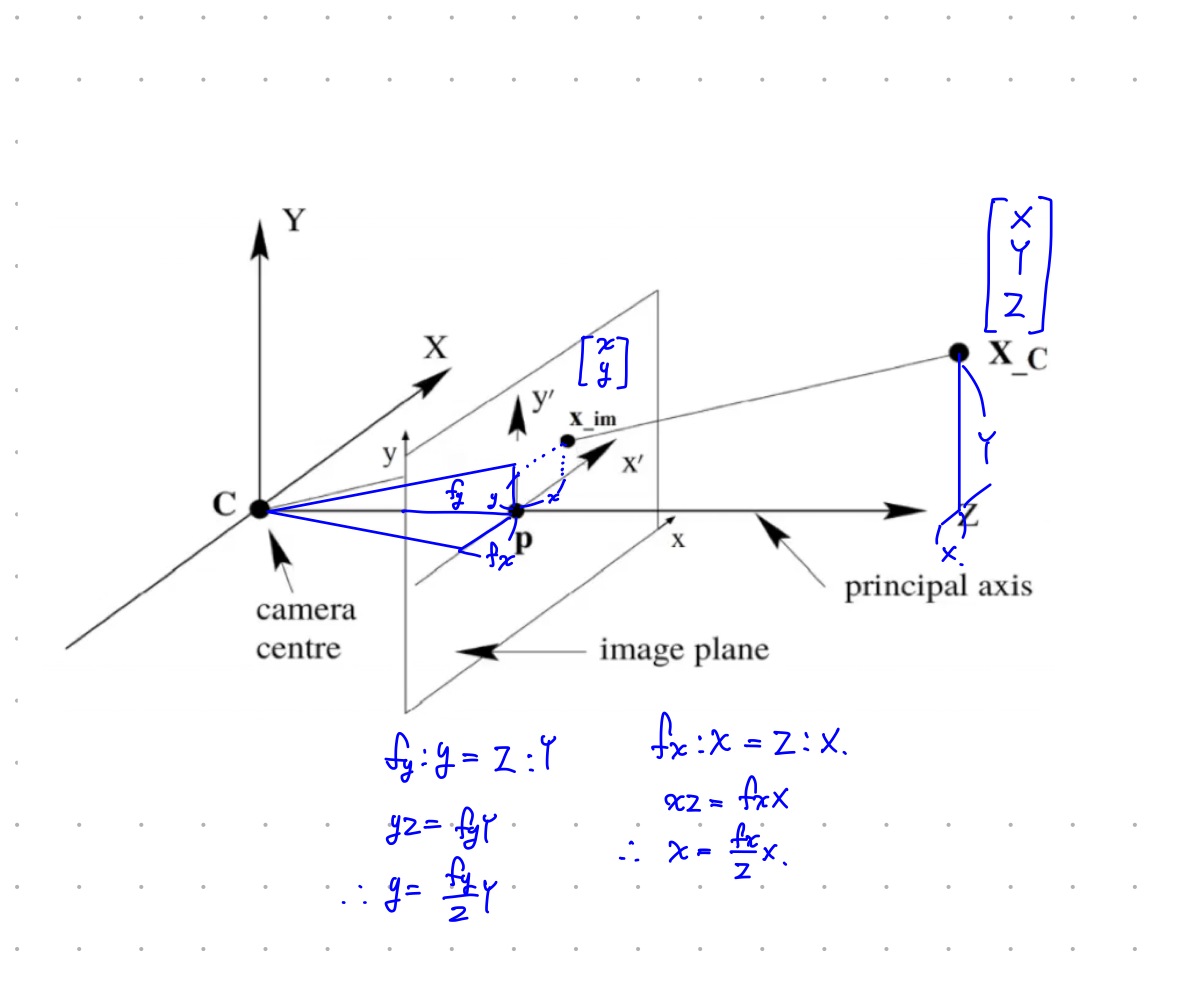
위 방법을 통해 2d 변환하였다. 하지만 아직 이미지 픽셀로 표현된건 아니다. C의 경우 이미지의 중심을 가로지르고 있다. 하지만 이미지의 원점(0, 0)은 이미지의 좌측 상단이다.

위 식처럼 principal point를 이미지의 중점으로 옮겨주는 과정을 통해 픽셀상의 한 점으로 나타낼 수 있다. 정확하게는 이미지의 중심 (Width/2, Height/2) 이어야 하지만 하드웨어 제작 과정에서 틀어지기 때문에 오류를 포함하게 된다.

위 식처럼 행렬의 형태로 표현이 가능하다. 이 행렬은 Intrinsic parameter를 나타내며, parameter를 찾는 과정을 camera calibration이라고 한다. 다시 말해 카메라 시점에서 본 3D 포인트를 2D 이미지 쌍의 포인트로 맺히게 하는 과정이라고 볼 수 있다.

정리

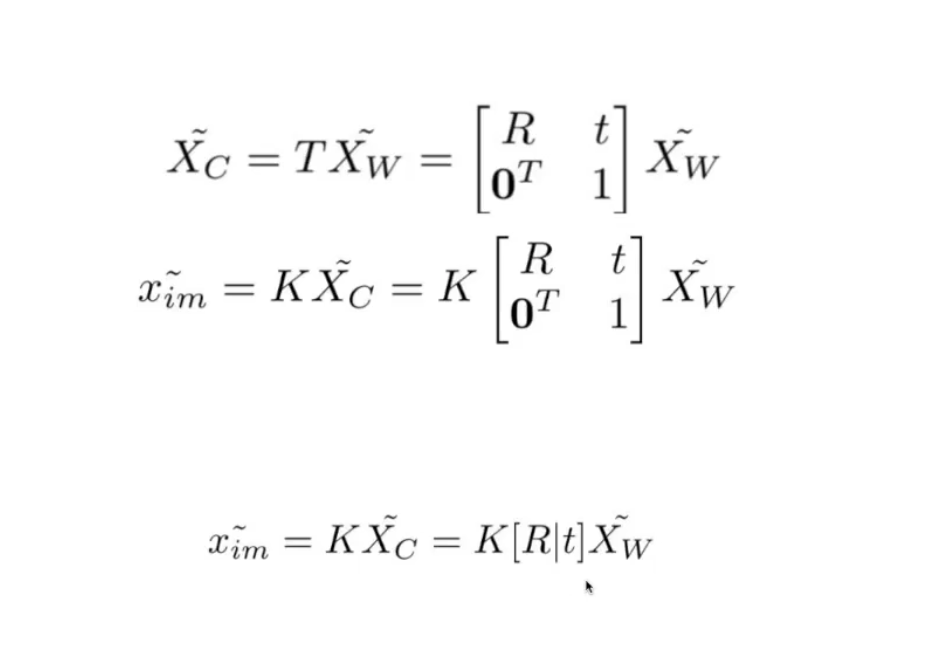
$\begin{bmatrix} R|t \end{bmatrix}$는 Extrinsic matrix를
$K$는 Intrinsic matrix 를 의미한다.