Projective geometry (사영기하학)
강체의 움직임(Rigid body motion)은 유클리드 기하학을 따른다. 또한 한 점만 이동시키는 affine geomotry와 닮음을 이용한 Similarity geometry 또한 기하 중 하나이다.

유클리드 공간에서의 평행한 두 직선은 무한의 거리에서 교차하지만 실세계에서는 이를 관측할 수 없다.
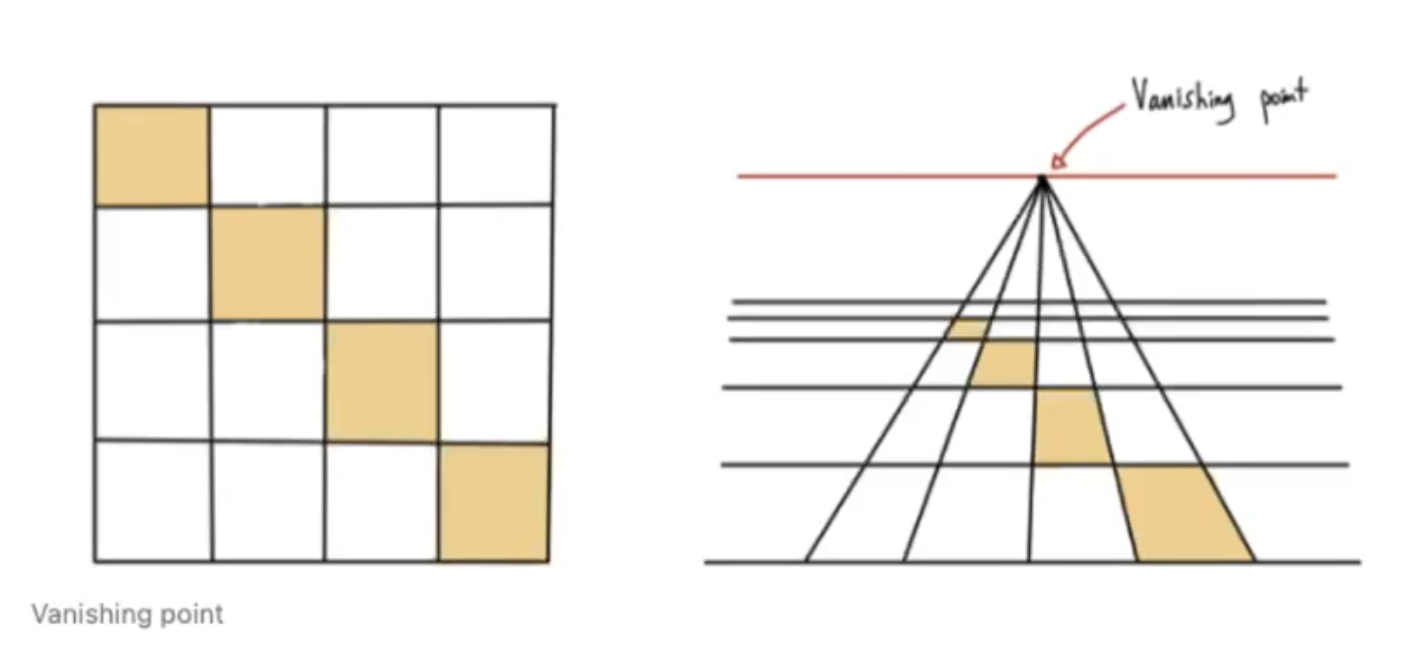
반면 이미지 상에서는 평행한 두 직선이 소실점을 통해 교차하는 것을 확인할 수 있으며 이를 통해 2D 공간의 소실점은 3D 세상의 무한의 위치에 대한 매핑이라고 생각할 수 있다.
N+1차원을 한 차원 작은 N차원으로 차원 축소를 할 때 통용되는 기하학이다. 이때, 3차원이 2차원으로 투영될 때 3차원에서 가지고 있던 scale이 필요하게 된다. 이를 표현하는 것이 바로 Homogeneous coordinate이다.
Homogeneous coordinates
Definition
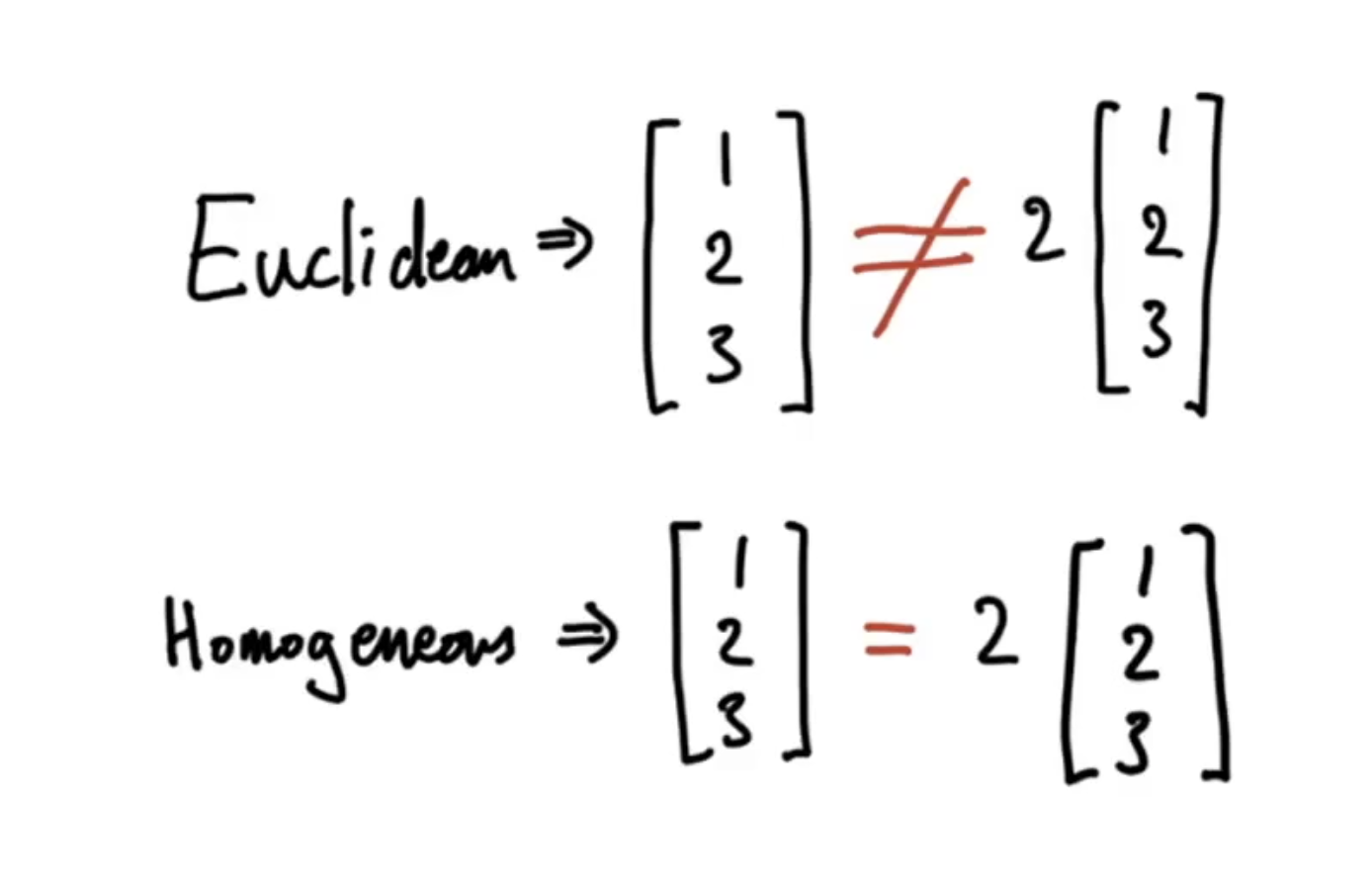
동차좌표계는 벡터에 어떤 스칼라를 곱해도 곱하기 전의 원래 벡터와 같은 값을 갖는다.

만약 x, y가 2, 4라고 할 때, 여기에 2를 곱하면 동차좌표계에는 4, 8, 2가 되고 이때 scale인 2로 동차좌표계를 나눠주면, 유클리드 좌표계와 동일한 것을 알 수 있다.
Projective space
유클리드 공간은 사영 공간에서 scale이 1에 해당하는 공간을 의미한다.

SO(3)와 SE(3) 좌표계에서 1에 해당하는 부분이 scale을 의미하는 것으로 Euclid 공간 인 것을 알 수 있다.
