[Cryptography(암호학)] 4주차-Message Authentication Codes

본 포스팅은 Coursera | Cryptography - Jonathan Katz 강의를 수강하며 정리했습니다.

1-1 Message Integrity

Cryptography 4주차 강의정리를 시작하겠습니다. 지난 시간에 PRF(Pseudorandom function)에 대해 살펴보며 key를 굳이 한 번만 사용하지 않더라도 동일한 메시지에 서로 다른 암호화 결과값이 나오는 암호화 scheme을 살펴봤습니다. 대표적인 block cipher의 한 종류로 AES의 여러 운용모델을 비교하며, CCA로부터 안전한지에 대해서도 공부했습니다.

1. Secrecy vs integrity

지금까지 공부한 암호화 scheme들은 message 자체가 알맞은 암호화 과정을 거쳐 잘 암호화되었는지에 대해 초점을 맞췄습니다. 공격 모델 또한 공격자에게 key를 유추할 수 없도록 하는 데에 집중했고요. 하지만 실제로 능동적인 공격자는 분명 존재할 것이고, 송신자가 만든 ciphertext를 조작하여 틀린 ciphertext를 원본 대신 전송할 수 있습니다.
어떤 message가 전송 도중에 수정되지 않고(not modified) 송신자가 보낸 message 그대로에 대한 암호임을 보장하는 개념을 integrity(무결성)이라고 합니다. 무결성을 검증할 수 있는 MAC(Message Authentication Codes)에 대해 알아보겠습니다.

그림은 MAC의 작동 방식을 설명하고 있습니다. MAC을 작동하는 큰 흐름은 tag를 만드는 알고리즘과 이를 검증하는 알고리즘으로 되어있습니다. 그림에서 Bob은 Alice에게 message $m$에 대하여 MAC 알고리즘 $Mac_k(m)$을 통해 생성한 tag $t$를 $m$과 함께 보냅니다. 이를 받은 Alice는 tag $t$가 잘 만들어졌는지 확인하는 알고리즘 $Vrfy_k(m, t)$를 통해 $m$이 $m'$으로 위조되었는지 여부를 확인합니다. 검증 알고리즘의 결과값이 0이 나오면 오류인 tag이고, 1이면 message가 변조되지 않고 잘 전송된 것을 의미합니다. 따라서 중간에 공격자에 의해 message와 tag가 각각 $m'$와 $t'$로 변조되더라도, 검증 알고리즘을 통해 무결성을 확인할 수 있습니다.

위 그림에서 무결성(integrity)를 판단할 때, message $m$을 그대로 전송했습니다. 이는 무결성(integrity)과 비밀성(secrecy)이 무관함을 뜻합니다. 다시 말해, 무결성이 검증된다고 비밀성이 보장되는 것이 아니고 반대의 경우도 마찬가지기 때문에 무결성과 비밀성은 독립적으로 봐야하는 개념입니다.

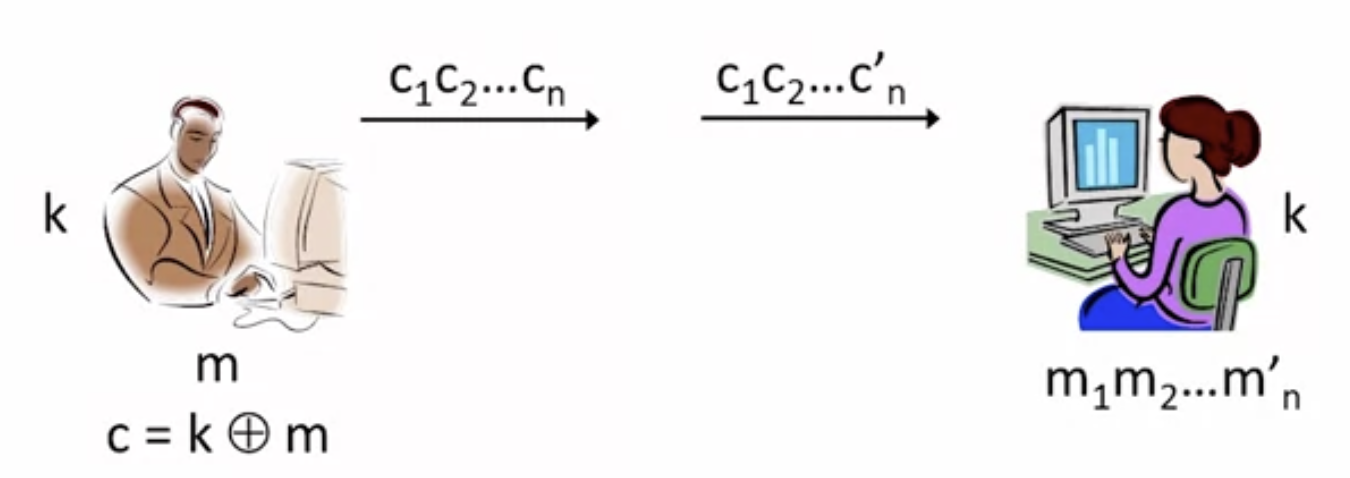
두 개념을 독립적으로 살펴보기 위해 secrecy의 일환인 암호화 scheme을 무결성(integrity) 인증 수단으로 사용한다고 가정해봅시다. 이 암호화 scheme이 OTP(One-Time Pad)라면 $c=k\oplus m$일 것입니다. 만약 어떤 공격자가 ciphertext $c_1,c_2,...,c_n$의 나열에서 $c_n$의 마지막 bit를 제외한 $c'_n$를 Alice에게 전송한다고 합시다. 이를 전송받은 Alice는 그렇게 받은 ciphertext가 Bob에게 온 것인지 아닌지에 대해 message 위조에 대한 구별 능력이 없습니다. 더군다나 비트 하나를 뺐을 뿐이지 제외된 비트를 제외한 다른 모든 문자에서는 정상적으로 암호화가 작동했기 때문에 그 무결성을 판단하기 더욱 어렵습니다. 즉 지금까지 배운 암호화 scheme 자체만 이용해서는 무결성(integrity)을 인증할 방법이 없습니다.

2. Message authentication code (MAC)

MAC은 key를 생성하는 $Gen$알고리즘, message에 대한 tag $t$를 출력하는 $Mac$알고리즘, tag가 잘 만들어졌는지 확인하는 $Vrfy$알고리즘까지 총 세 개의 PPT 알고리즘으로 이루어져 있습니다. 정의는 아래와 같습니다.

$Gen(1^n) = k\;$ (Assume $|k| \ge n$)
$Mac_k(m) = t\;$ ($m \in \{0,1\}^*$)
$Vrfy_k(m, t) = 1$
$\Leftrightarrow$ For all $m$ and all $k$ output by $Gen$, $Vrfy_k(m, Mac_k(m)) = 1$

3. Security

| Threat model & security goal

MAC에 대한 안전성 검증을 해보도록 하겠습니다. 먼저 threat model과 security goal에 대해 알아봅시다. MAC에서는 'Adaptive chosen-message attack' 이라는 공격 모델을 사용합니다. Adaptive chosen-message attack에서는 공격자가 선택한 임의 message를 수신자가 인증하도록 유도할 수 있다고 가정합니다. Security goal은 'Existential unforgeability', 즉 공격자가 수신자가 아직 인증하지 않은 message에 대해 유효한 tag를 위조할 수 없어야 합니다.

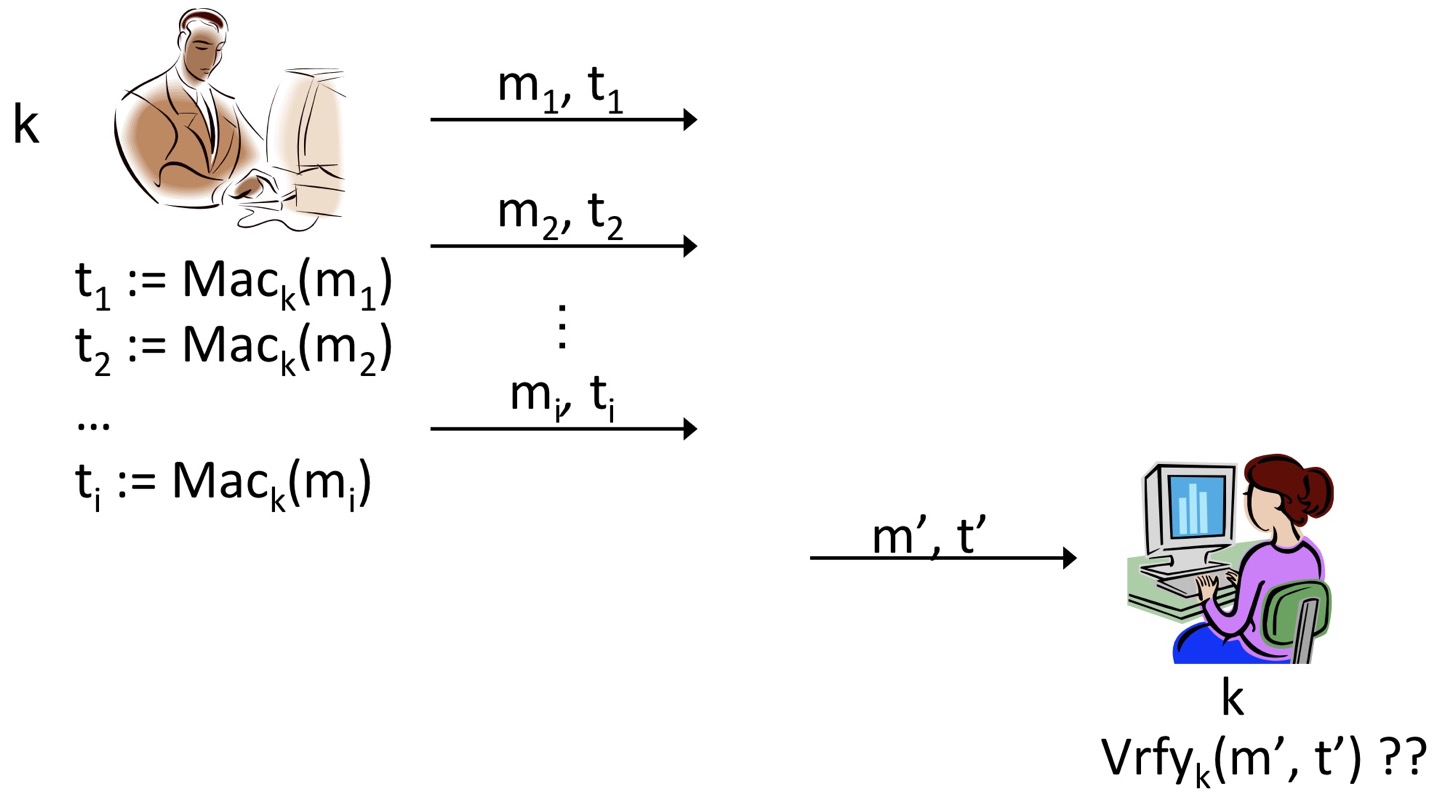
그림으로 더 쉽게 이해해봅시다.공격자와 수신자는 서로 상호작용이 가능합니다. 공격자가 요청한 message가 i개라고 할 때, 송신자는 message ($m_1,m_2,...,m_i$)에 대하여 각각 tag를 생성해 전송합니다. Tag를 확인한 공격자는 본인이 요청한 message 이외의 어떤 message에 대해 tag를 생성하여 이 tag가 $Vrfy_k(m',t')=1$이 나오지 않도록, 즉 공격자가 새로운 유효한 tag를 생성하는 것이 불가능하도록 해야합니다.

| Formal definition

공격 과정에 대해 정리하면 아래와 같습니다.

$\begin{aligned} Fix& \;\; Scheme \; \mathrm{\Pi} \;\;\;\; Attacker \; A \\ For&ge_{A, \Pi}(n): \\ 1.& \;\; k \leftarrow Gen(1^n) \\ 2.& \;\; A \;interacts \; with \; an \; oracle \; Mac_k(\cdot) \; in \;|M| \\ 3.& \;\; A \; output \; (m, t) \\ 4.& \;\; A \; succeeds, \; and \; the \; experiment \; evaluates \; to \; 1, \\ & \;\;\;\;\; if \; Vrfy_k(m,t) = 1 \; and \; m \notin M \end{aligned}$

위 과정에서 공격자는 2번 과정을 반복하며 임의의 메시지에 대한 태그를 생성받을 수 있고, $Forge_{A, \Pi}(n)$는 공격자 $A$가 $Vrfy_k(m, t)=1$을 맞출 확률을 나타냅니다.

이때, MAC에 대한 secure는 아래와 같습니다.

4. Replay attacks

무결성(integrity)을 검증할 수단으로 MAC을 살펴보았습니다. 하지만 MAC은 재생 공격(replay attacks)을 막을 순 없습니다. 재생 공격(replay attacks)은 공격자가 송신자로부터 전송받은 메시지를 단순 반복할 때 발생합니다. MAC을 사용하여 "1,000 만원 전송"이라는 메시지에 대해 무결성 검증을 했더라도, 공격자가 위 메시지를 10번 반복하여 전송할 경우 1억 원 상당의 금액을 갈취할 수 있게 됩니다. 현실에서는 재생 공격(replay attacks)이 충분히 일어날 수 있으므로 이에 대한 조치가 필요합니다.

1-2 A fixed-length MAC

1. Intuition & Construction

MAC 알고리즘 중 tag $t$를 생성하는 알고리즘 $Mac_k(m)$은 $Gen$에서 제공하는 key가 사용됩니다. Key가 필요한 이유는 서로 다른 메시지를 공격자가 요청했을 때 같은 알고리즘을 사용해서 생길 수 있는 규칙성을 감추기 위함입니다. 그래서 keyed function이 필요합니다. 지난 시간에 keyed function은 PRF(pseudorandom function)를 정의할 때 봤었는데요, MAC의 $Mac_k(m)$ 알고리즘 또한 PRF와 비슷한 속성을 가지고 있습니다. 그래서 $Mac_k(m)$를 PRF의 한 종류인 block cipher처럼 message와 key의 길이가 정해져 있는(fixed-length) function이라고 가정하고 재정의하겠습니다.

$MAC \; \Pi$ :

• $Gen$ : choose a uniform key $k$ for $F$
• $Mac_k(m) = F_k(m)$ ($F$ be a length-preserving pseudorandom function (PRF))
• $Vrfy_k(m, t)$ : output 1 iff $F_k(m)=t$

이때 F가 PRF(pseudorandom function)라면 $\Pi$ 는 secure MAC 입니다. 이에 대한 증명도 진행해 보겠습니다.

2. Proof of reduction

이번에도 proof of reduction 방식으로 증명을 해보겠습니다. 조금 전 재정의한 MAC $\Pi$를 공격하는 공격자 A가 있다고 합시다.

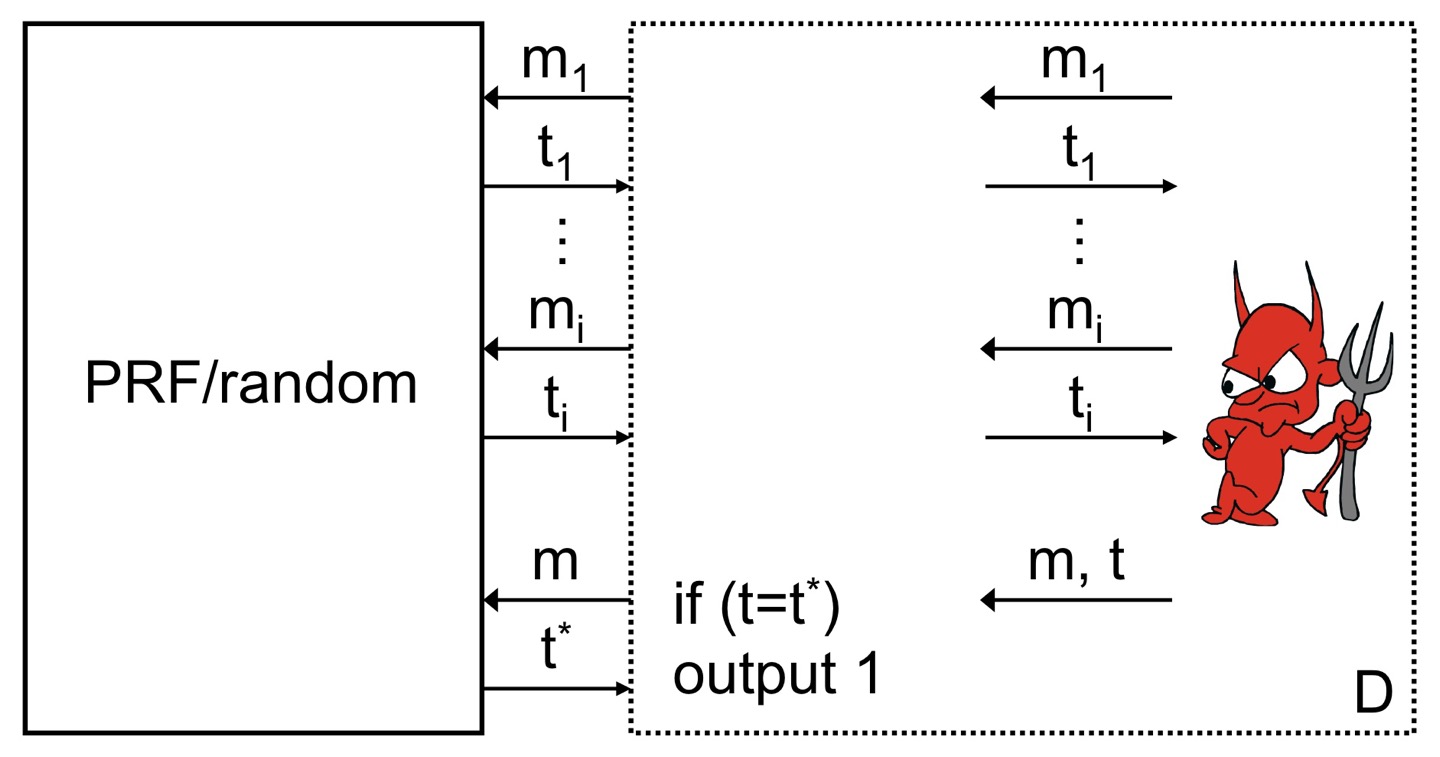
공격자는 PRF 혹은 uniform key $k$로 random function 혹은 PRF로 된 오라클과 상호작용합니다.
공격자는 $m_1$부터 원하는 만큼 i 번의 message를 요청할 때마다 oracle을 통해 tag를 반환받습니다. 이 과정이 끝나면 공격자는 새로운 message $m$에 대한 tage $t$를 만드는데, 공격자가 직접 만든 tag $t$와 외부 오라클로부터 만들어진 tag $t'$가 동일하면 D 알고리즘은 1을 반환하고, 공격자가 실패할 경우 0을 반환합니다.

함수 $F_k$ 와 상호작용하는 알고리즘 $D$ 가 존재할 때, $D$ 가 1을 반환할 확률은 공격자의 위조 가능 확률과 동일합니다.

앞서 우리는 함수 $F_k$가 입력값과 출력값의 길이가 고정된 PRF라고 가정했습니다. 따라서 PRF에서 나온 출력값은 uniform한 성질을 가질 것입니다. 공격자가 최종적으로 알고싶은 message $m$은 기존에 공격자가 요청했던 ${m_1, m_2,...,m_i}$에는 없는 값입니다. PRF에서 나온 출력값은 아무리 상호작용을 하더라도 uniform하기 때문에 예측이 불가합니다. 따라서 $Pr[D^{F_k} \; outputs \; 1] = 2^{-n}$ 확률을 만족합니다. 이를 통해 우리는 MAC scheme $\Pi$가 secure 함을 보일 수 있습니다.

3. Drawbacks?

MAC에 대한 scheme $\Pi$가 안전한지에 대해 살펴보았습니다. 그렇다면 실제로도 PRF를 사용하여 만든 $\Pi$는 안전할까요? 현실에서 PRF는 block cipher로 주로 구현된다고 했습니다. 가장 대표적인 block cipher인 AES는 128bits의 블록 크기를 지니고 있습니다. Block cipher는 입출력값의 길이가 동일하므로, 그럼 MAC 알고리즘에서 출력되는 tag의 길이도 128 bits가 될 것입니다. 하지만 만약 매우 긴 message에 대한 MAC을 만들어야 할 경우, 이 길이적 제한은 큰 단점이 됩니다. 비효율적이기도 하고요. 그래서 길이가 길고 128 bits 이외 다양한 message에 대해 어떻게 MAC을 만드는 것이 효율적인지에 대해 고민해 볼 것입니다.

2-1 CBC-MAC

앞선 강의에서 언급한 MAC의 한계를 극복하기 위해 이번에는 임의의 길이의 message는 어떻게 MAC을 만드는 것이 좋은지, 그리고 그에 대한 안전성을 어떻게 보장하는지에 대해 다뤄보겠습니다. 대표적인 해결책이 바로 CBC-MAC입니다.

1. CBC-MAC

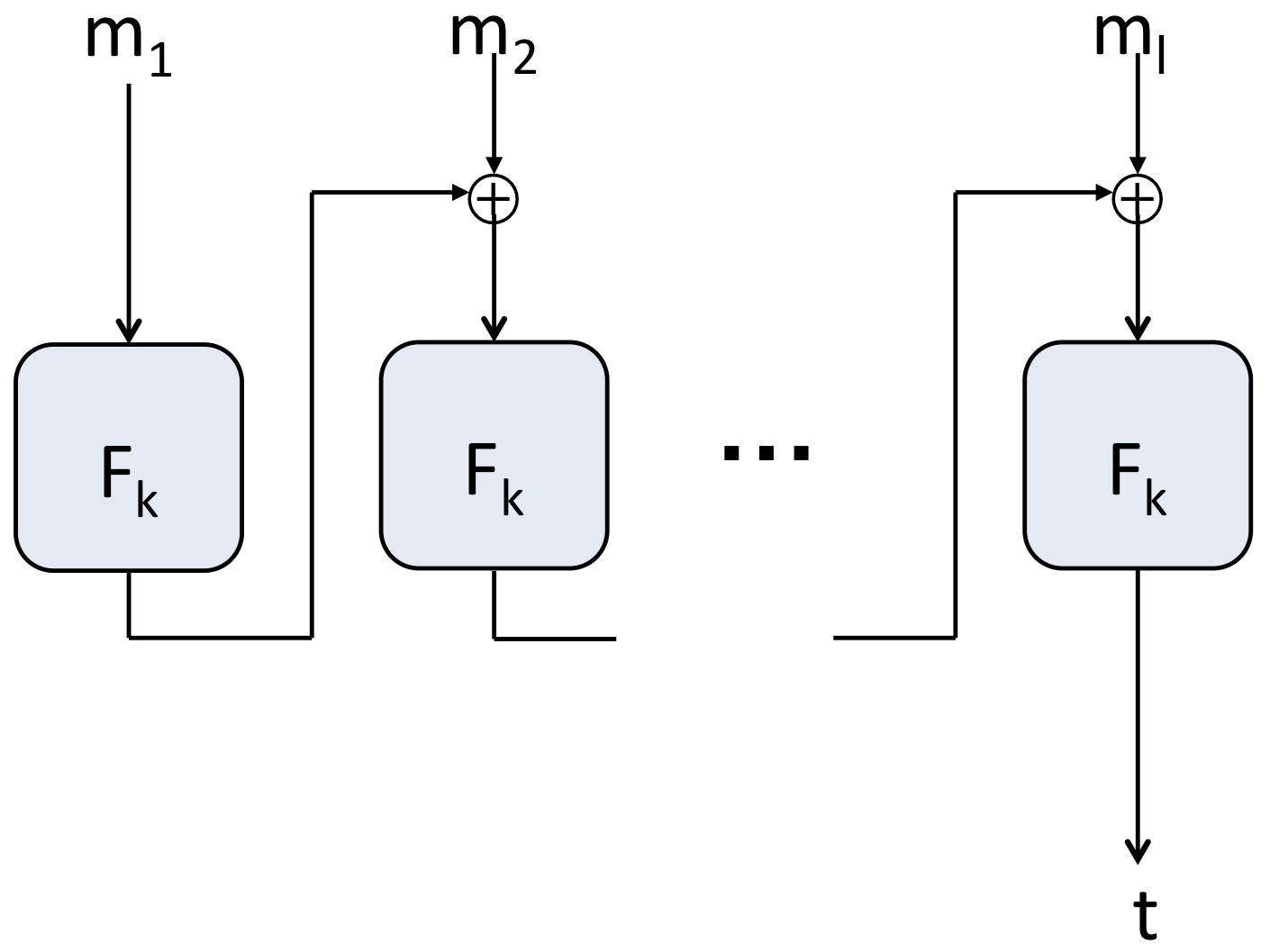
CBC-MAC은 CBC-mode와 비슷한 방식으로 동작합니다. Message 블록이 $m_1$에서 $m_l$($l$은 블록 개수)까지 주어질 때, $F_k$를 메시지 블록에 적용한 값을 XOR하여 다음 블록 암호에 전달하는 방식입니다. 마지막 message 블록까지 이 동작을 반복하고나면, 블록 하나의 길이와 동일한 길이의 tag $t$가 출력될 것입니다.

2. CBC-MAC vs CBC-mode

CBC-MAC는 CBC-Mode encryption과 매우 유사하지만, CBC-MAC의 security에 몇 가지 차이점이 있습니다. 첫 번째 차이점은 CBC-MAC가 결정론적(determistic)이라는 것입니다. CBC-MAC은 CBC-mode와 다르게 초기화 벡터(IV)가 없기 때문입니다. CBC-mode는 IV가 있어서 같은 메시지라도 다른 출력값을 줄 수 있지만, CBC-MAC은 IV가 없어 determistic합니다.(만약 사용을 하더라도 모든 bit가 0인 IV를 사용한다고 합니다.) MAC은 random으로 생성될 이유가 없습니다. 암호화가 위변조 되었는지 확인하는 용도로 사용되기 때문에, 오히려 초기화벡터(IV)를 이용하면 값이 불안정하기 때문에 더 위험해질 수 있습니다. 두 번째 차이점은 CBC-MAC은 마지막에 생성된 값만을 tag로 사용하지만, CBC-mode는 블록 단위로 모든 결과를 연결하여 출력한다는 점입니다. 하지만 안전성을 위한 목적은 두 가지가 동일하겠죠?

3. Security of (basic) CBC-MAC?

이제 CBC-MAC의 안전성에 대해 살펴봅시다. CBC-MAC에서 사용하는 F가 PRF(pseudorandom function)이라면, 블록의 개수와 그 블록의 메시지 길이 또한 고정된 값일 겁니다. 이때 블록 개수를 $l$, 블록 당 메시지 길이를 $n$이라고 합시다. 그럼 블럭 사이즈 $n$과 블럭 개수 $l$의 곱인(l$\cdot$n)는 메시지의 총 길이가 됩니다. 이때 수신자와 송신자는 메시지를 보내기 전 블록 개수 $l$에 대해 사전에 합의를 해야합니다. 이에 대해 사전 합의가 없다면 $l$이 메시지의 총 길이와 직결된 변수이므로 MAC이 잘 동작하더라도 소통이 잘 되지 않을 수 있습니다. 안전성에 문제가 생기는 것이죠.

4. CBC-MAC extentions

우리의 목표는 길고 다양한 길이의 메시지에 대해 효율적인 MAC을 생성하는 것입니다. CBC-MAC으로 마지막 블록의 결과값만을 tag로 생성한다는 점에서 효율적인 tag를 만드는 목표는 달성했습니다. 이제 CBC-MAC의 확장판을 통해 다양한 $l$이어도 충분히 MAC을 만들 수 있는 방법을 알아보겠습니다.

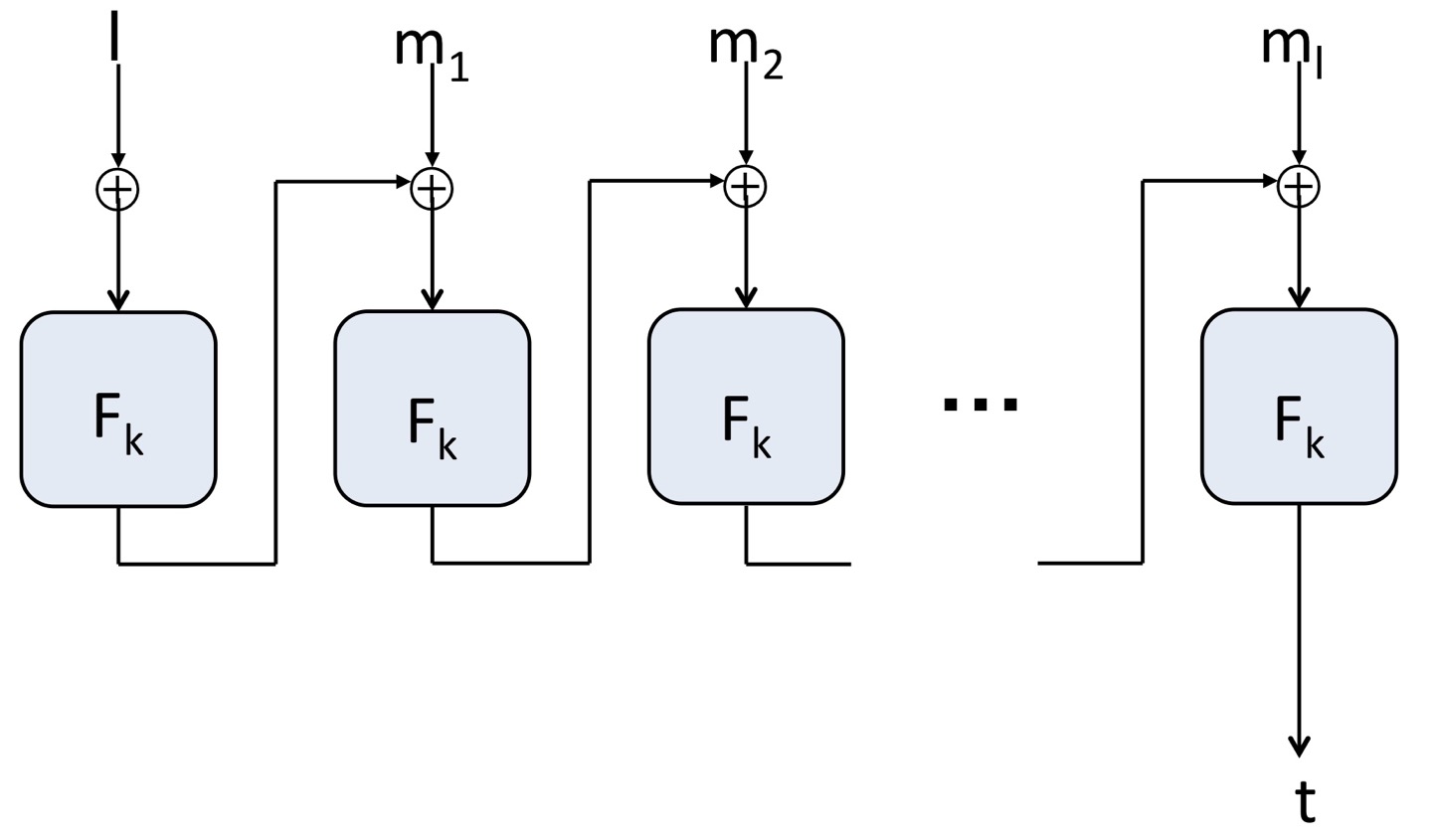
앞에서 문제가 되었던 것은 $l$에 대한 사전합의가 불확실하다는 점이었습니다. 이를 해결하기 위해 메시지 블록 가장 앞에 $l$을 붙여 보낼 수 있습니다. 다음 그림은 메시지 앞에 파라미터 l을 먼저 CBC 하여 MAC을 구하는 알고리즘이다. 위처럼 기존 CBC-MAC의 안전성을 보완하며 MAC을 살필 수 있습니다.

2-2 Hash functions

앞으로 뒤에서 MAC의 또 다른 종류인 HMAC을 볼텐데, 이번 강의에서는 HMAC에 사용되는 hash function에 대해 먼저 공부하고 넘어갑시다.

1. Hash functions

해시함수(Hash functions)란 임의의 길이를 가진 input 값을 고정된 길이의 짧은 값으로 매핑된 함수를 말합니다. 대표적으로 SHA-256이 많이 사용됩니다. 해시함수를 거친 함숫값을 다이제스트(digest)라고 하는데, 아무리 긴 message라고 할지라도 동일한 길이의 짧은 다이제스트로 빠져나옵니다.

해시함수는 크게 두 종류가 있습니다. 해시함수는 keyed function으로도, unkeyed function으로도 정의할 수 있는데, 보안성을 높이기 위해서는 keyed function으로 사용하는 게 바람직하지만, 현실적으로는 key를 매번 설정해주기 힘들기 때문에 unkeyed function으로 주로 사용됩니다.

2. Collision-resistance

충돌 저항성(Collision-resistance)은 해시함수의 안전성을 판단하는데 중요한 지표입니다. 해시함수에서 collision의 의미와 정의를 먼저 살펴보겠습니다.

Hash function (H)에서 서로 다른 input x와 x’이 있을 때, H(x) = H(x’) 이라면 이 x와 x’ pair를 collision이 생겼다고 표현합니다. H (해시 함수)가 collision-resistant 하다는 것은 이러한 collision을 찾는 것이 현실적으로 불가능하다는 것을 말합니다.

3. Generic hash-function attacks

해시함수에 대한 가장 대표적인 공격으로 generic hash-function attacks이 있습니다. 해시 함수의 다이제스트의 길이가 n이라고 할 때, 나올 수 있는 다이제스트의 가짓수는 $2^n$입니다. 그럼 $H(x_1)$부터 $H(x_{2^n+1})$까지 가능한 $x$값을 대입해 넣으면 적어도 하나의 겹치는 쌍이 나올 것입니다. 해시함수 다이제스트의 가능한 경우의 수 이상의 입력값을 넣었기 때문에 비둘기집 원리에 의해 반드시 한쌍은 충돌이 일어날 수밖에 없는 것이죠.

4. Birthday attacks

Generic hash-function attacks에 기반하여 한 집단에서 collision이 나타날 확률을 더 직접적으로 나타낸 공격이 있습니다. 바로 birthday attack입니다. Birthday attack에서는 해시함수 H에 $x_1$부터 $x_{2^{n/2}}$ 종류의 input을 넣을때 collision이 발생할 확률은 50%가 된다고 말합니다.

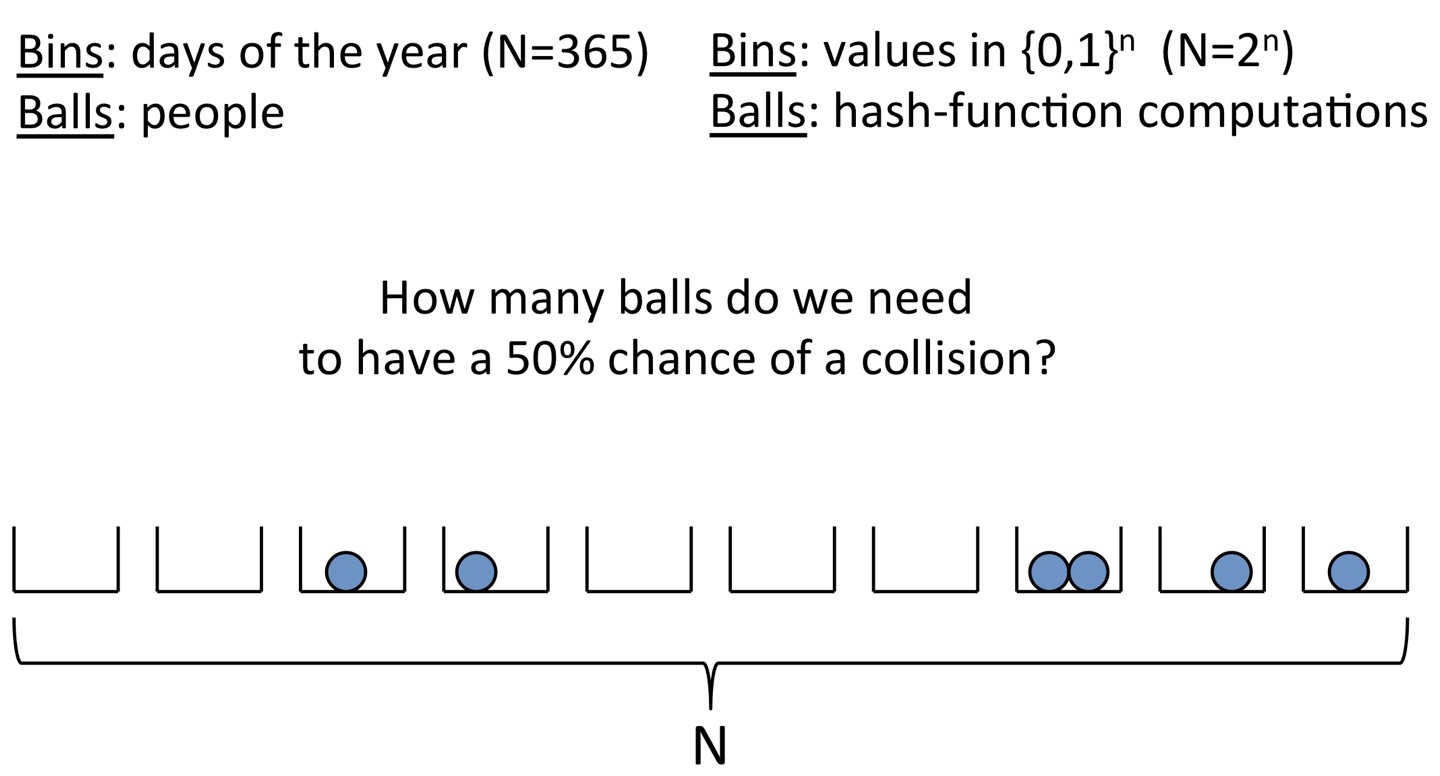
위 그림에서 공을 담는 통이 N개 있다고 합시다. 공을 던져 어떤 통에 들어갈 확률이 uniform하다면, 그 확률은 $1/N$입니다. 이때 1년이 365일이니 N을 365라고 가정합시다. 공은 사람이라고 생각해볼게요. 물론 충돌이 생기지 않을 수도 있지만, 공이 $\sqrt{365}$ 개 이상이라면 높은 확률로 동일한 통에 들어가는 적어도 두 개의 공이 생깁니다. 이를 birthday paradox로 설명할 수 있습니다.

Birthday paradox에서는 동일한 생일자인 사람을 찾기 위해 몇 명의 사람들과 생일을 공유해야 하는지에 대해 다룹니다. 일차원적인 생각으로는 적어도 366명이 있어야하지만, 실제로는 제곱근의 사람이 있다면 50%의 확률로 같은 생일자인 사람 쌍이 나옵니다.

결론적으로 굳이 해시함수에서 collision을 찾기 위해 $2^n+1$ 만큼의 x값을 넣어보지 않아도 collision을 더 쉽게 찾을 수 있다는 이야기입니다.

5. Hash functions in practice

해시함수의 역사는 아래 간략한 설명으로 대체하겠습니다.

• MD5 : 1991년 개발; 128-bit output; 2004년 collision 발견
• SHA-1 : 1995년 개발; 160-bit output; 2017년 collision 발견
• SHA-2 : 256-bit or 512-bit output
• SHA-3/Keccak : SHA family중 가장 different design; 224, 256, 284, 512-bit output

3-1 HMAC

해시함수에서 봤으니, 다시 본론으로 돌아가 MAC(메시지 인증 코드)에 대해 살펴보겠습니다. 2-1 강의에서는 짧거나 긴 고정 길이에 대한 message의 MAC을 만들기 위해 CBC-MAC을 사용했습니다. 이번엔 임의의 길이에 message에 대하여 생성할 수 있는 MAC의 한 종류로, 앞서 강의에서 살펴본 해시함수를 기반으로 만들어진 HMAC에 대해 살펴보겠습니다.

1. Hash-and-MAC

해시함수는 고정된 다이제스트값이 나온다는 것이 큰 특징이었습니다. 이 점을 이용해 어떤 길이의 값을 넣든 동일한 길이의 출력값이 나온다는 해시함수의 특징을 이용해 MAC을 만들어봅시다. Hash-and-MAC을 살펴봅시다. (HMAC과는 다른 모델입니다)

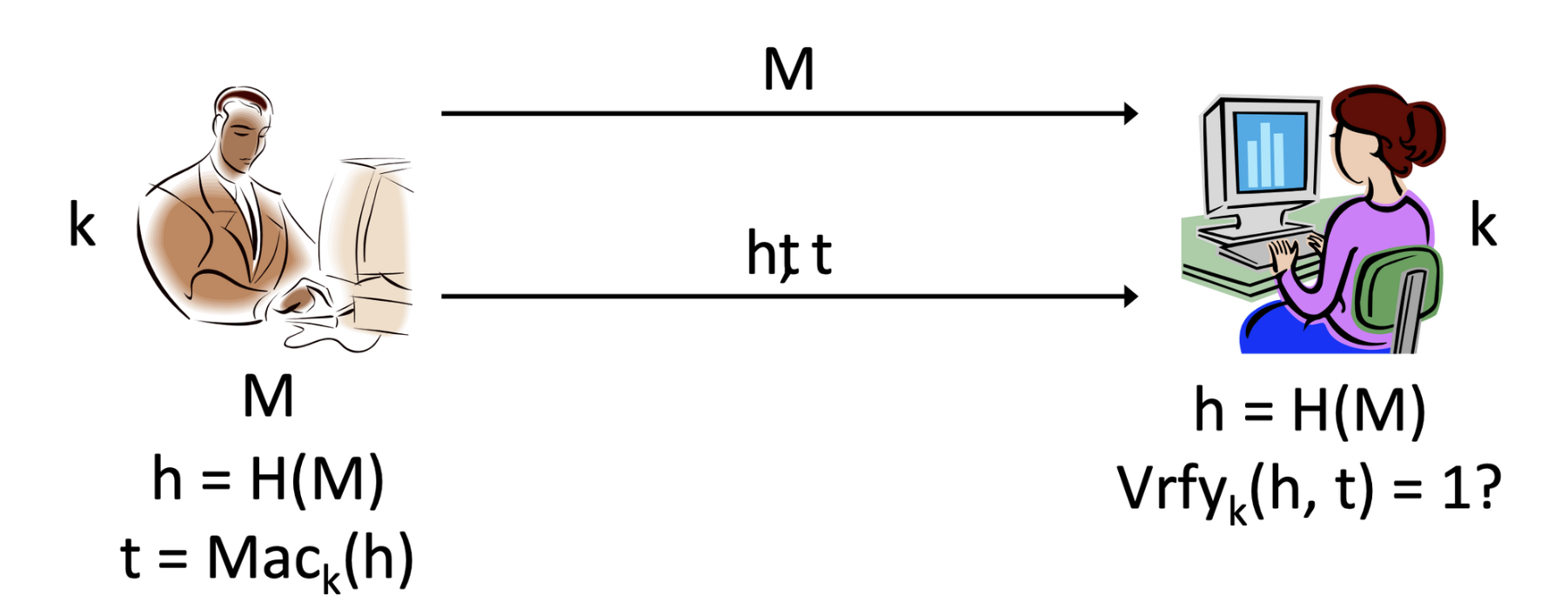
Hash-and-MAC을 주고받는 방식에 대해 살펴보겠습니다. Bob은 message $M$에 대하여 해시함수 $H(M)$을 계산한 다이제스트 $h$ 값을 얻습니다. 그렇게 만든 $h$를 MAC 알고리즘에 적용하여 tag $t$를 생성합니다. Alice는 message $M$과 tag $t$를 전송받아 $M$을 해시함수에 적용하고, 그렇게 얻은 다이제스트값 $h$를 $Vrfy_k(h,t)$ 알고리즘에 넣어 그 결과가 1이 나오는지 확인합니다. 1이 나오면 변조되지 않은 값임을, 0이면 변조된 값임을 나타내어 integrity(무결성)를 확인할 수 있습니다.

2. Security

위처럼 만들어진 Hash-and-MAC은 안전할까요? 만약 MAC이 고정 길이 message에 대해 안전하고 해시함수 H가 collision-resistant의 성질을 가지고 있다면, hash-and-MAC은 임의 길이의 message에 대해 안전한 MAC일 것입니다. 우리는 이를 더 간단하게 증명하기 위해 proof sketch를 먼저 살펴보겠습니다.

| Proof Sketch

송신자가 $M_1, M_2,..., M_i$에 대하여 메시지 인증을 하려고 합니다.

이때 공격자가 이를 확인하고 위조한 $(M, t)$를 만든다고 가정합시다. 물론 위조한 message는 그 어떤 $M_i$와 같은 값이면 안됩니다. 이 때 두 가지 경우가 생깁니다.

$H(M)=H_(M_i)$ for some i

첫 번째는 공격자가 위조로 만든 해시가 $M_i$의 어떤 해시값과 같을 때입니다. 즉, collision이 일어났을 때입니다. 이 경우, 공격자는 $M_i$를 계산한 tag를 재사용하기만 하면 위조를 만들어낼 수 없습니다. 여기서 요점은 공격자가 해시함수의 collision을 먼저 발견했다는 것이죠. 하지만 앞서 전제에서 해시함수가 collision-resistance라고 가정했으므로, $M$과 $M_i$의 해시가 같은 쌍을 찾는 것은 불가능합니다.

$H(M)\neq h_i$ for all i

두 번째는 $M$의 해시 다이제스트가 모든 i에 대해 $h_i$와 같지 않은 경우입니다. 즉 공격자가 만들어낸 위조문이 유효하다면, 이전에 송신자로부터 받은 $h$에서 어떠한 단서를 찾았다는 것입니다. 하지만 이는 MAC이 fixed length에 대하여 안전하다는 가정이 전제되었기 때문에 $h$로부터 유효한 단서를 얻는 것은 실현 불가능합니다.

| Instantiation

그럼 현실에서 해시함수를 이용한 MAC을 적용해봅시다. 앞서 우리는 fixed length message에 대하여 block cipher를 이용했습니다. 이 block cipher와 해시함수를 합하여, 해시함수의 다이제스트를 블록단위로 나누어 MAC을 실행합니다.

3. HMAC

하지만 이에는 문제점이 있습니다. 우리가 MAC에 사용하는 AES에서 입력값과 출력값은 128 bits로 고정되어 있는데, SHA-1 같은 경우 다이제스트가 160 bits로 블록에 모든 다이제스트의 비트를 담기에 부족했던 것입니다. 그래서 HMAC이 등장합니다. HMAC은 다이제스트 길이만큼 블록을 나누어 진행하는 방식입니다.

3-2 Authenticated Encryption

지금까지 integrity(무결성)에 대해 공부했습니다. 무결성을 인증할 수 있는 수단으로 MAC에 대해 살펴보았고, 실제 사용되는 다양한 MAC의 종류도 살펴보았습니다. 언제나 강조하듯 integrity(무결성)은 secrecy(비밀성)와 다른 개념입니다. 하지만 실제 암호를 구현할 때는 이 둘을 모두 만족시켜야 여러 측면에서 안전한 암호를 완성할 수 있을 것입니다. 이 강의에서는 secrecy와 integrity 모두를 만족하는 authenticated encryption에 대해 살펴보겠습니다.

1. Encrypt and authenticate

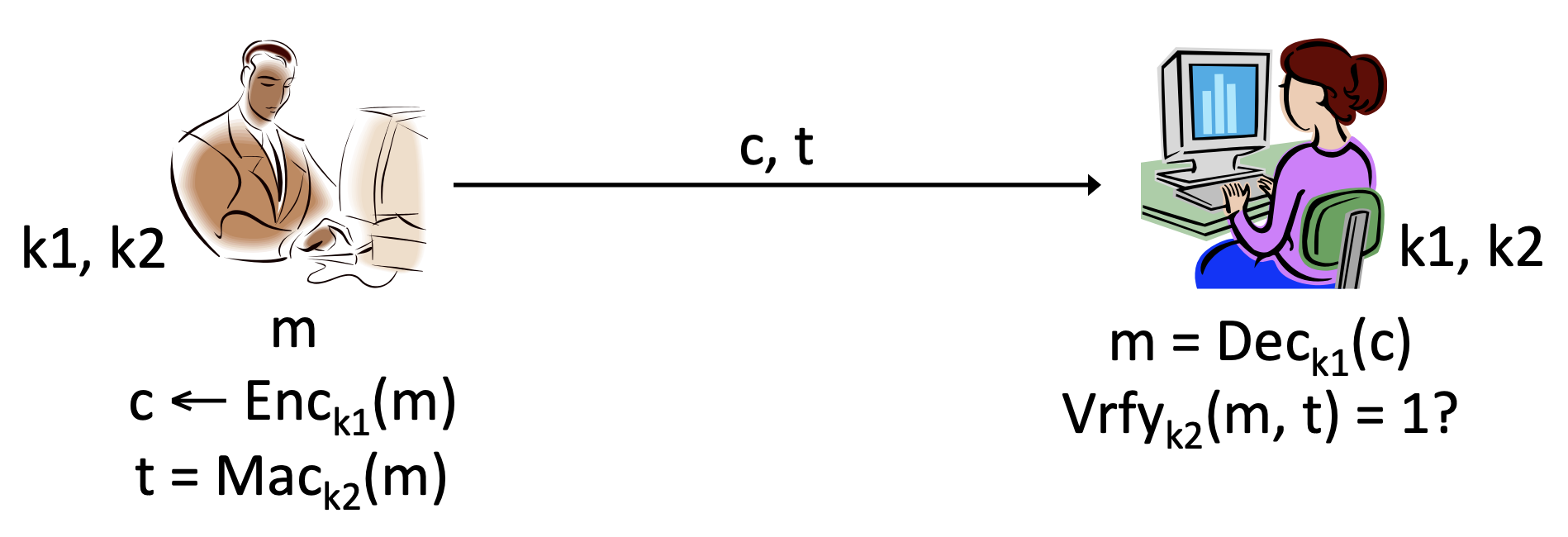
먼저 Encrypt and authenticate입니다. 이 방법은 message $m$에 대해 ciphertext $c$와 tag $t$를 각각 생성한 뒤, 이를 수신자에게 전송하는 방법입니다. 수신자는 이렇게 받은 $c$와 $t$에 대하여 각각 secrecy와 integrity를 검증합니다.

| Problem

위 과정은 어찌보면 타당해 보이지만, 사실 문제점이 있습니다. MAC 알고리즘은 어떤 입력값에 대해 언제나 결정론적인(deterministic) 결과값을 제공합니다. 즉, 같은 message를 전송했을 때 tag의 값이 동일하기 때문에 tag $t$ 자체가 메시지에 대한 정보로 유출되는 것입니다. 따라서 안전성이 떨어지게 됩니다.

2. Encrypt then authenticate

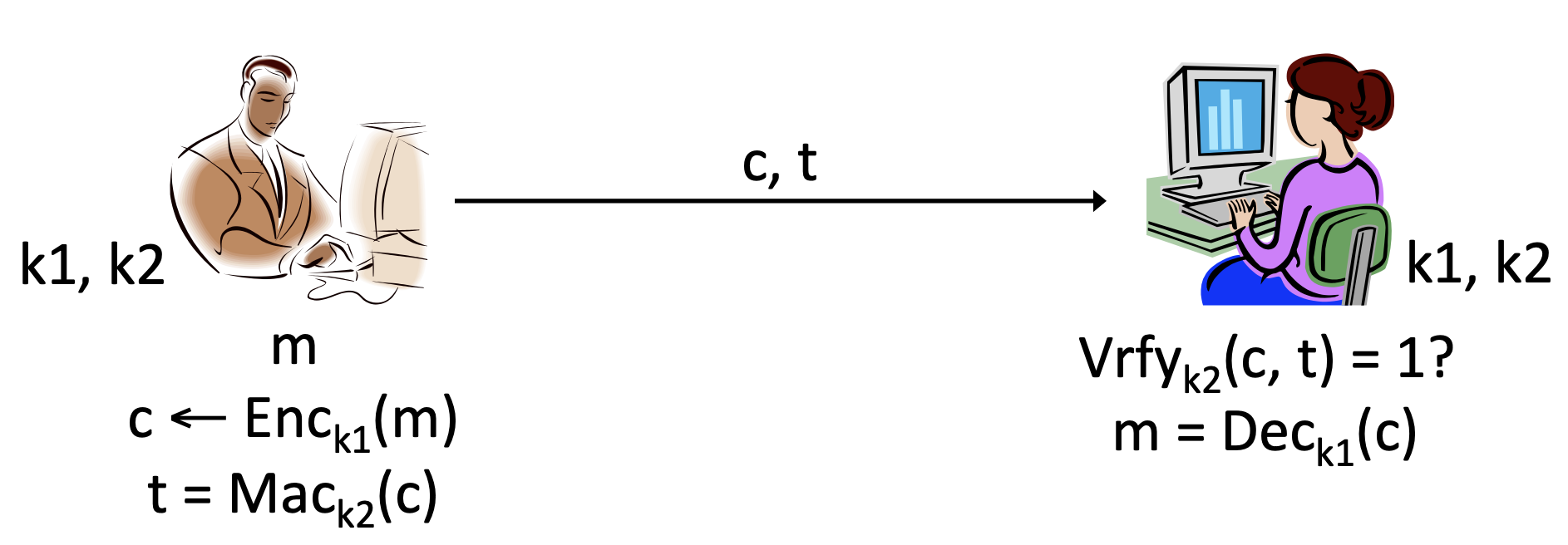
두 번째는 Encrypt then authenticate입니다. 이 방법은 tag와 ciphertext 생성을 독립적으로 하지 않고, message $m$에 대한 ciphertext $c$를 입력값으로 하여 tag $t$를 생성합니다. $c$는 동일한 message여도 random의 성질을 지닌 결과값이 나오기 때문에 tag로부터 message에 대한 정보가 유출되는 것을 막을 수 있습니다. 이때 암호화 알고리즘이 CPA-secure하고 MAC이 안전하다면, 이 조합 또한 안전합니다.

3. Authenticated encryption

만약 어떤 scheme이 위 조건들을 모두 만족한다면 우리가 지금까지 봤던 어떤 암호화 scheme보다 더 안전할 것입니다. 왜냐하면 공격자의 입장에서 위변조도 못할 뿐더러 message에 대한 정보도 알 수 없으니까요.

이러한 속성을 가진 암호화 scheme을 Authenticated encryption이라고 합니다. Authenticated encryption은 CPA-security와 CCA-security까지 만족합니다.

3-3 Secure Communitacion Sessions

Authenticated encryption의 개념을 배웠으니 이제 구현을 통해 송신자와 수신자 사이에 소통을 해봐야죠! 이번 강의에서는 secrecy와 integrity를 모두 겸비한 encryption을 모두 만족시키며 소통하는 방법을 살펴보겠습니다. 먼저 용어 정리를 하고 넘어갑시다.

• “Securely” = secrecy(비밀성)와 integrity(무결성)를 모두 만족한 것
• “Session” = 두 당사자가 서로 암호를 주고받는 상태

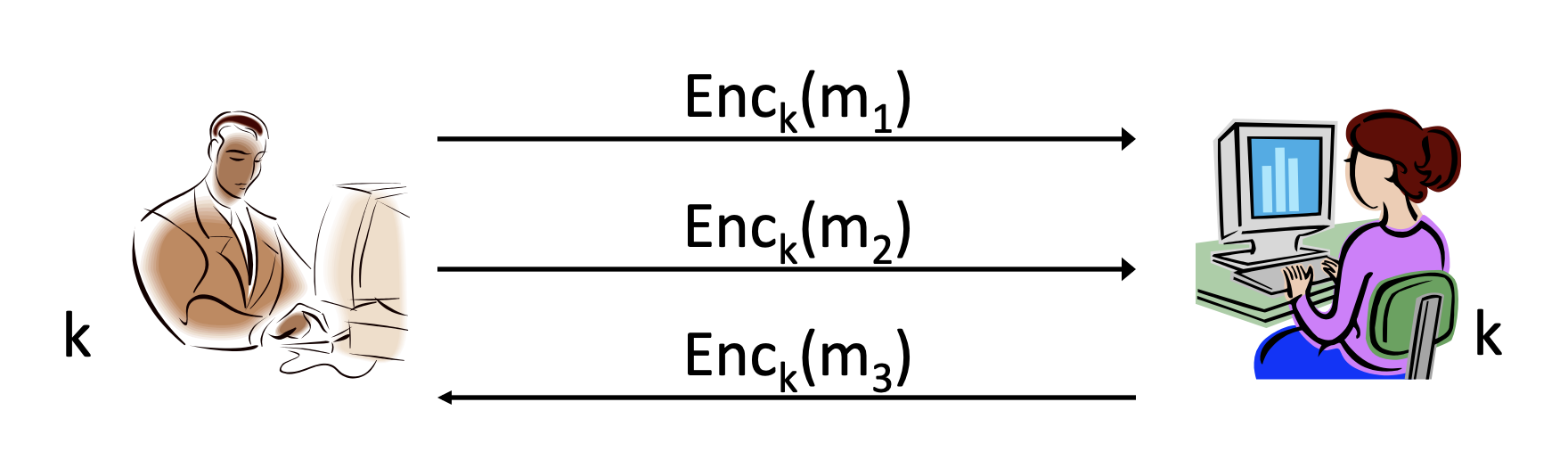
위 그림에서 두 당사자는 key $k$를 사전에 공유하고 있고, message $m_1$과 $m_2$에 대한 암호문을 보내고 $m_3$에 대한 암호문을 받았습니다. 두 당사자들은 authenticated encryption을 사용하고 있으므로, 공격자가 암호문의 일부를 변경한다면 잘못되었는지 아닌지에 대해 당사자들이 판단할 수 있습니다. 그렇다면 authenticated encryption은 언제나 안전할까요? 사실 authenticated encryption도 특정 공격에 대해 굉장히 취약합니다.

1. Replay attack

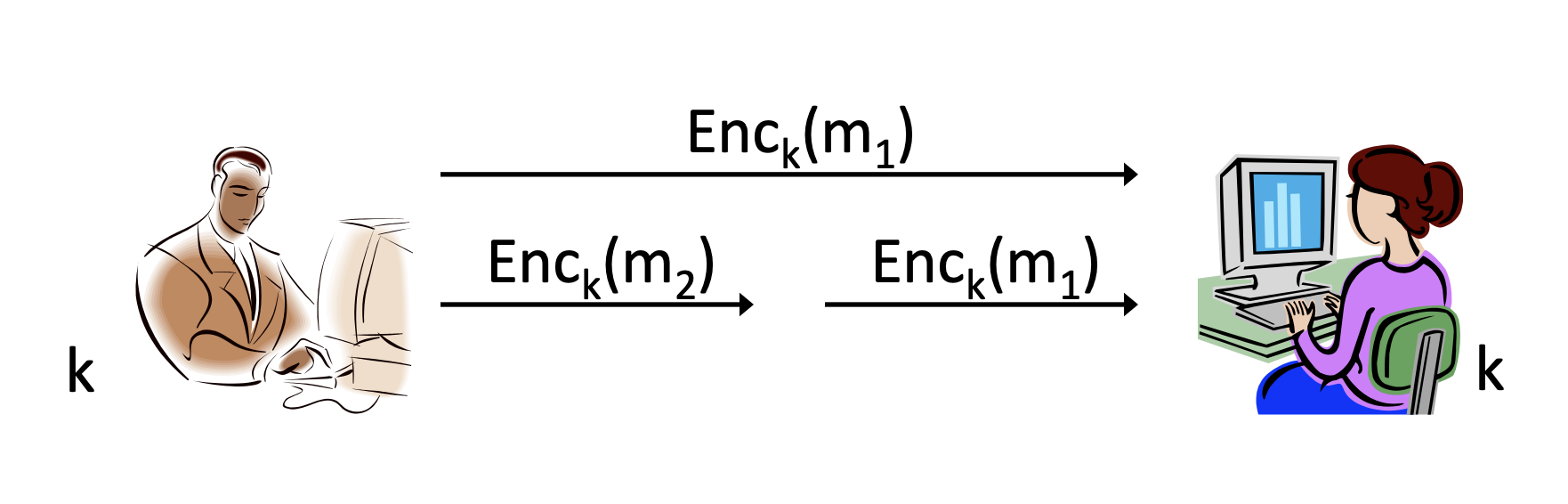
첫 번째 공격은 replay attack입니다. 송신자의 암호문 자체를 반복하여 수신자가 본래 암호문과 다른 암호문을 받도록 하는 것입니다. 위 그림에서 Bob은 $m_1$과 $m_2$에 대한 암호문을 각각 보내려고 했으나, 공격자는 $m_1$을 두 번 반복함으로써 본래의 목적과 다른 의도로 전송되었습니다.

2. Re-ordering attack

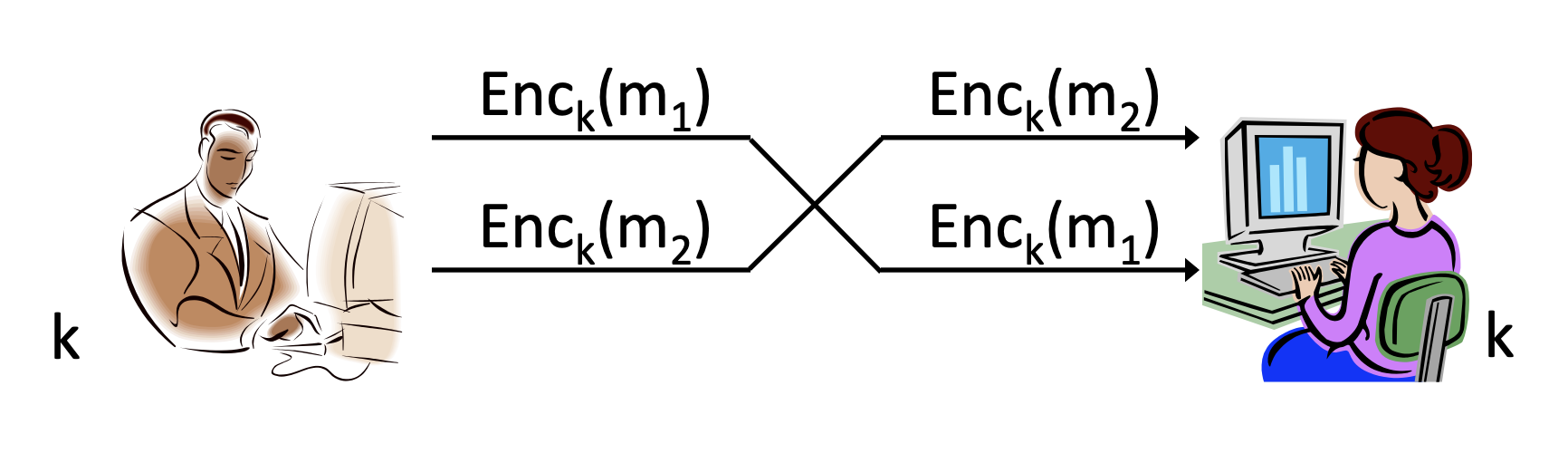
두 번째는 re-ordering attack입니다. 송신자의 암호문 순서를 바꾸는 공격 방법입니다. 위 그림에서 Bob은 $m_1$ 다음에 $m_2$를 보내려고 했지만, 공격자가 네트워크 스케쥴링을 제어할 수 있다면 충분히 두 암호의 순서를 바꿔 Alice에게 전송할 수 있습니다.

3. Reflection attack

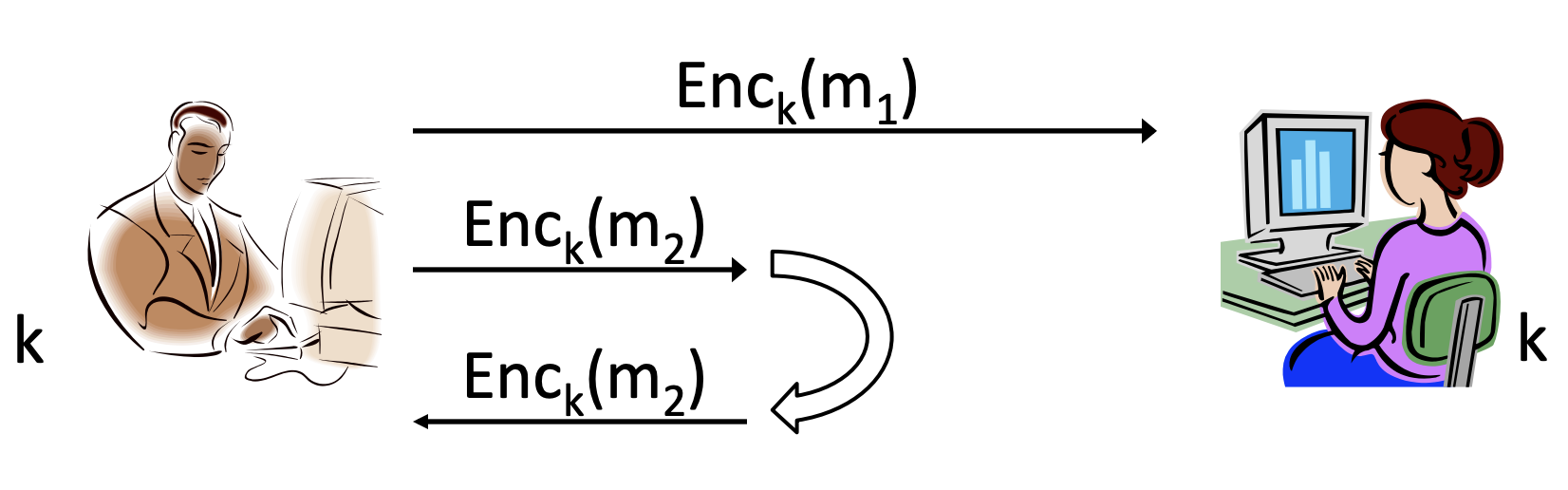
세 번째 공격은 reflection attack입니다. 이 공격은 수신의 주체를 바꿔버리는 공격입니다. 위 그림에서 Bob은 밥은 Alice에게 $m_1$을 보낸 후 $m_2$를 보내려고 했지만, $m_2$가 Alice에게 도달하기 전에 $m_2$에 대한 암호문을 다시 Bob에게 전달하여 Bob 입장에서는 Alice가 전송한 것처럼 만들었습니다.

4. Secure sessions

위에서 본 세 공격의 공통점은 이렇게 공격을 시행한다고 해도 송수신자 입장에서는 이를 알 방법이 없다는 것입니다. 위와 같은 공격을 예방하기 위해서는 어떻게 해야할까요? 문제가 되는 것은 암호문 전송 순서와 보낸 이 였으므로, 메시지 순서와 보낸 사람에 대한 정보를 함께 보내면 해결할 수 있을 것같습니다.

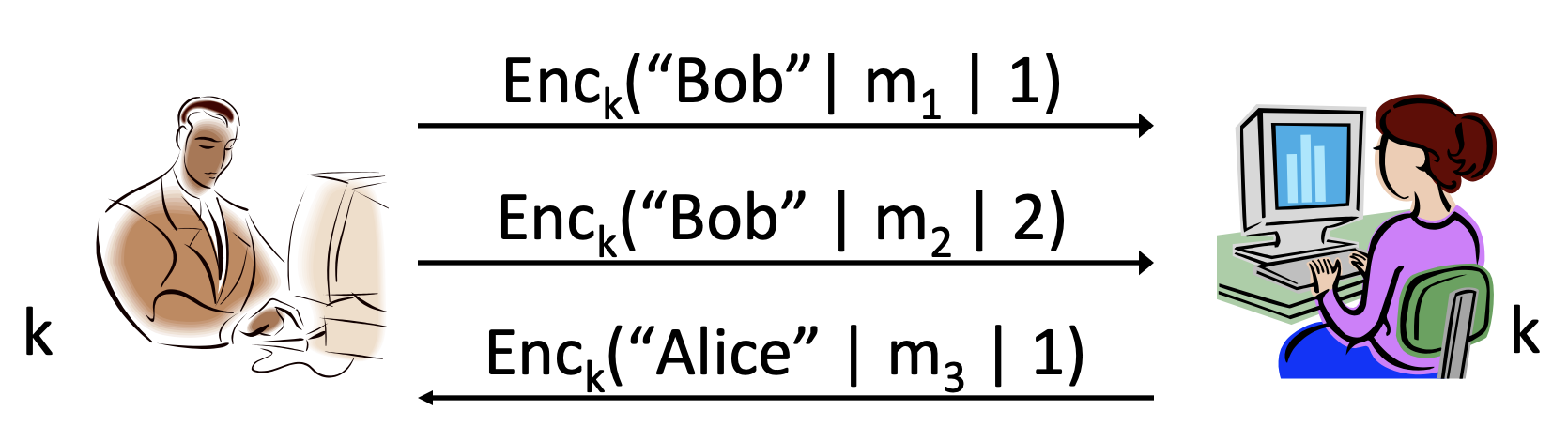
아래 그림에서는 이번에 보낸 이의 이름과 보낸 순서를 연결하여 함께 전송했습니다. 이때 메시지 순서는 counter, 보낸 이의 정보를 identity라고 합니다.

---

이를 바탕으로 private key에 대한 secure session에 대해 정의가 마무리 되었습니다! (고생했습니다..) 다음 시간에는 비대칭키 암호화의 근간이 되는 number theory에 대해 살펴보겠습니다.