[Cryptography(암호학)] 3주차-Private-Key Encryption

본 포스팅은 Coursera | Cryptography - Jonathan Katz 강의를 수강하며 정리했습니다.

1-1 Stronger Security Notions

Cryptography 3주차 강의정리를 시작하겠습니다. 지난 시간에 OTP(one time pad)의 한계를 살펴봤습니다. key의 길이가 message의 길이보다 크거나 같아야 한다는 조건과 key 하나 당 하나의 message만을 암호화해야 한다는 조건이었습니다. Perfect security의 개념을 조금 현실적으로 접근하며, OTP의 한계를극복하기 위해 등장한 PRG, 그리고 PRG의 기반이 되는 pseudorandom의 개념 또한 살펴봤습니다.

PRG를 통해 message의 길이보다 작은 길이의 key를 뽑는 것이 해결되면서, OTP의 첫 번째 조건의 한계는 극복한 듯 보입니다. 하지만 두 번째 조건, 하나의 key 당 하나의 message만을 암호화해야 한다는 조건은 아직까진 변함이 없습니다. 해당 포스팅에서는 이 한계를 극복할 수 있는 방법을 찾아보겠습니다.

그 전에 잠시 지난 포스팅 2주차 이야기를 되짚어보겠습니다. Perfect security를 정의할 때, 두 가지의 definition이 필요했습니다.

security goal : 공격자의 행동을 방지하려는 목표
e.g. 공격자가 random 문자열과 암호화 scheme을 거친 문자열을 구분할 수 없다
Threat model : 공격자가 취하는 공격 방법 (CPA, CCA . . .)

OTP의 첫 번째 한계를 극복하기 위해 저희는 perfect security의 개념에서 computational indistinguishability의 개념으로 오기까지 security goal을 계속해서 조절해나갔습니다. 이제 security goal을 동일하게 설정한 채로 위협 모델(threat model)을 강화해보겠습니다. 아직 감이 잘 안 잡히겠지만, 아래 위협 모델을 파악해보면 이해가 잘될 겁니다.

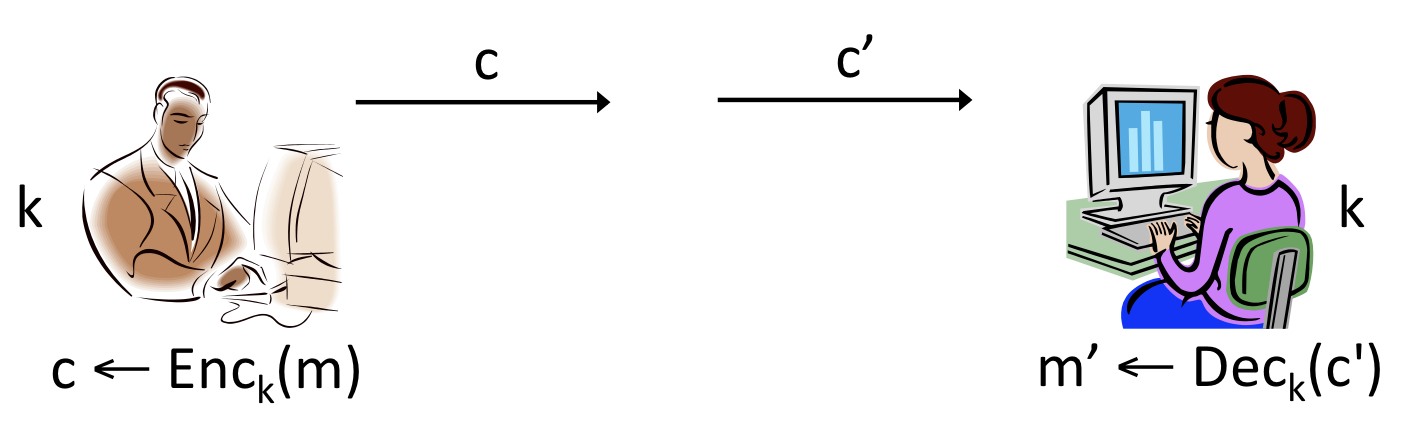
1. Single-message secrecy

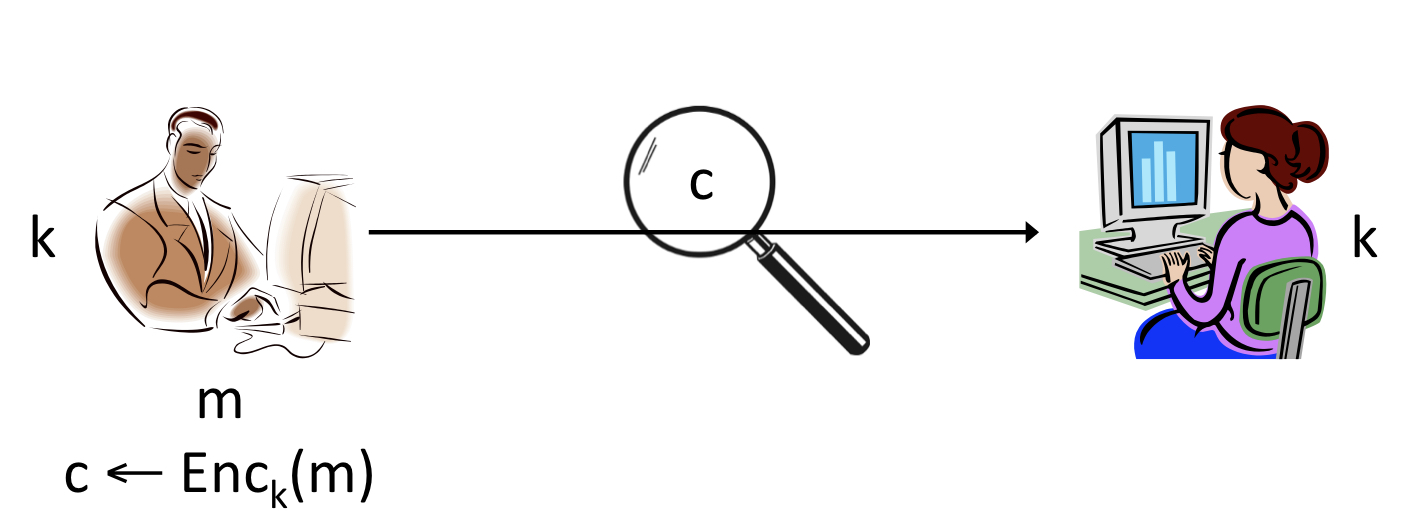
위 그림은 Alice와 Bob이 하나의 message $m$에 대하여 ciphertext $c$에 대한 암호화를 진행하는 단일 메시지 암호(single-message encryption)입니다. 하지만 하나의 key에 대해 여러 개의 message를 암호화했을 때 발생하는 문제점과 이를 해결할 방안을 살펴보기 위해서는 message 두 개 중 하나를 구분하는 모델이 아니라 두 개 이상의 여러 message에 대해 같은 key를 사용하는 모델에 대해 살펴봐야 합니다. 즉 단일 메시지 암호(single-message encryption)로는 해결책을 살펴보기 어렵습니다. 현실적으로도 단 하나의 메시지만을 암호화하기 위한 scheme은 유용하지 않기도 하고요.

2. Multiple-message secrecy

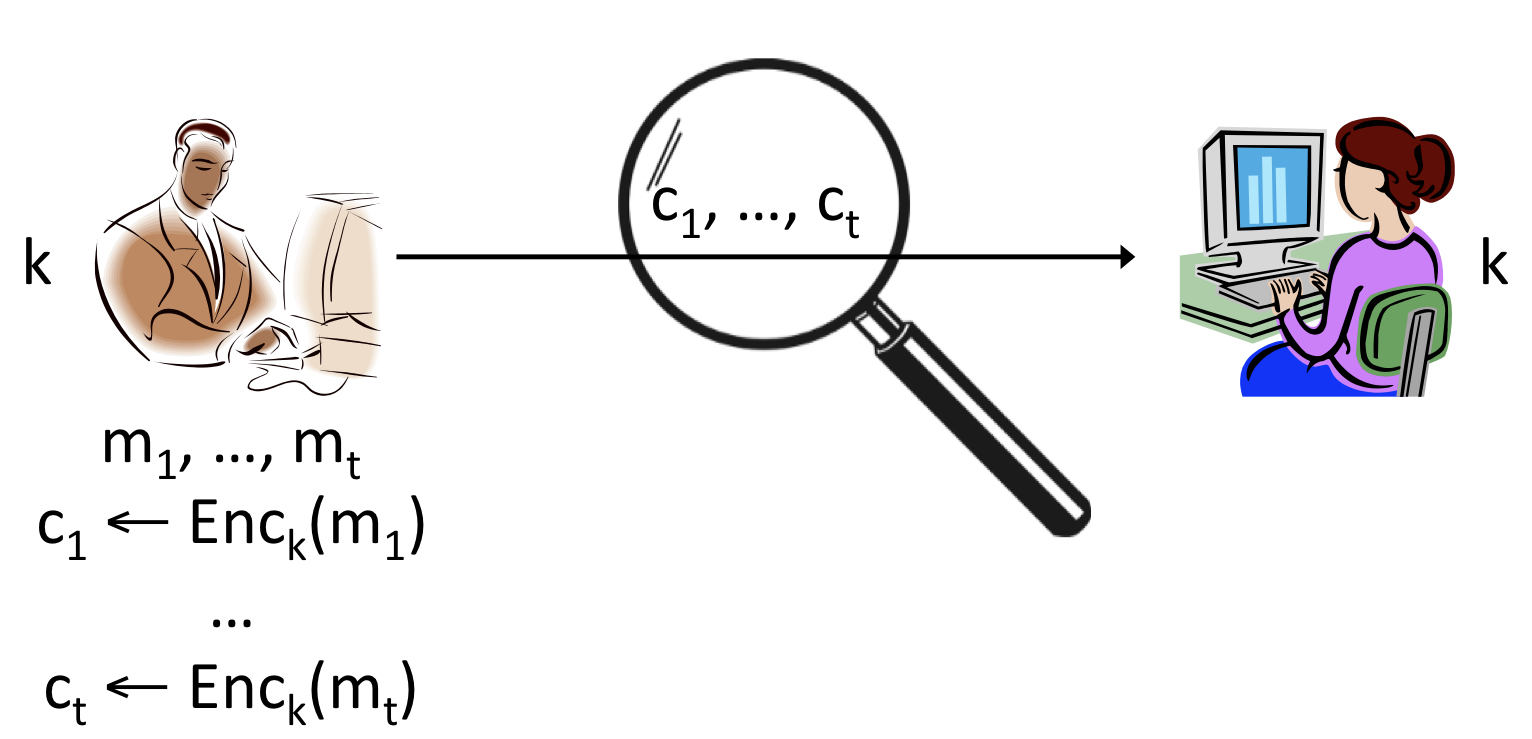
위 그림은 Alice와 Bob은 두 개 이상의 message $m_1,...,m_t$에 대하여 ciphertext $c_1,...,c_t$에 대한 암호화를 진행하는 다중 메시지 암호(multiple-message encryption)입니다. 돋보기에 해당하는 공격자는 두 당사자 Alice와 Bob 사이에서 전달되는 t개의 ciphertext c를 모두 도청할 수 있습니다. 물론 message가 무엇인지는 말 수 없는 상태겠죠. 이때 security goal은 "ciphertext가 주어졌을 때 공격자가 message에 대한 정보를 알 수 없다면 안전하다" 입니다.

이렇게 다중 메시지 암호(multiple-message encryption)를 위협 모델(threat model)로 정하는 것이 하나의 key에 대한 여러 message의 암호화 진행방식을 살펴볼 우리의 목표를 충족하기엔 충분하지만, 현실적으로 살펴봤을 때 여러 개의 메시지가 오가며 암호화가 진행되기 위해서는 시간적으로 충분한 상태여야 합니다. 공격자 입장에서도 언제 두 당사자 간 암호화가 진행될지 모르니 시간을 두고 여지없이 기다려야할 때도 있을 것입니다. 그런 점에서 약간의 제약이 존재합니다. 그래서 다중 메시지 암호(multiple-message encryption)보다 더 강력한 모델을 설정할 겁니다. 바로 chosen-plaintext attack, 다른 말로 CPA-security입니다.

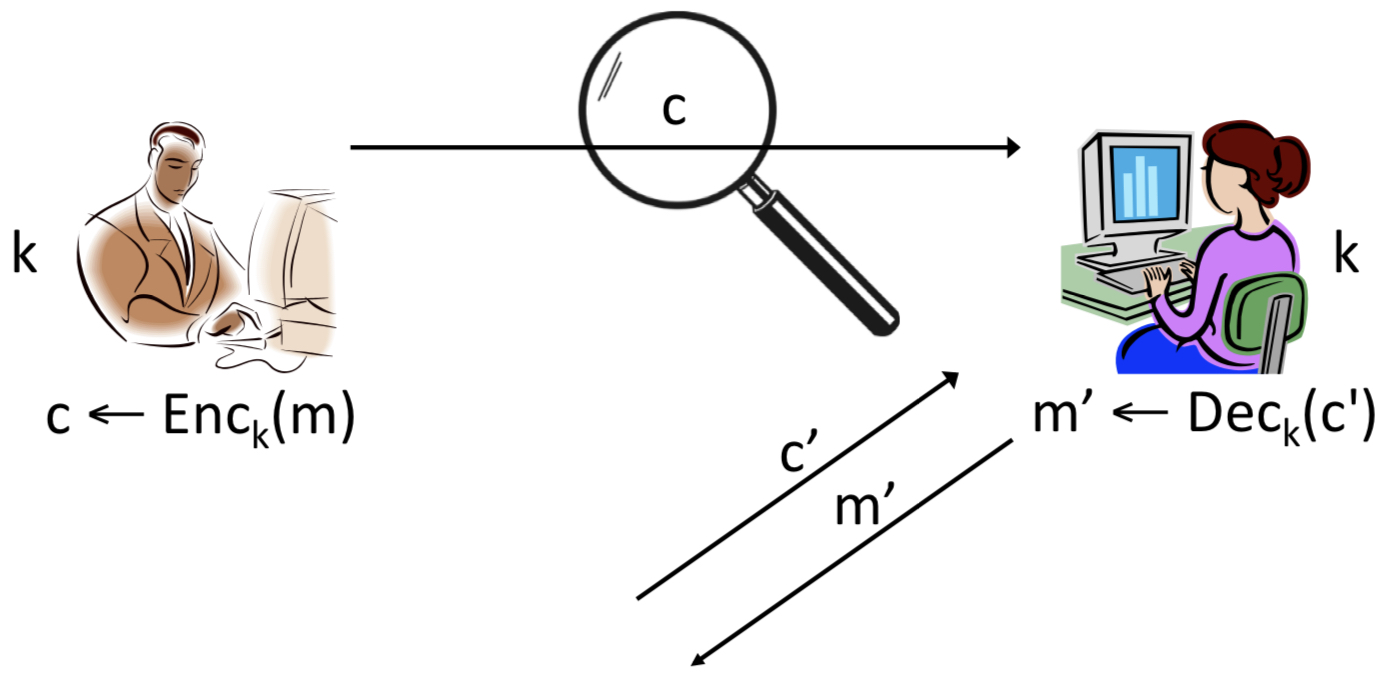
3. CPA-security

CPA attack에 대한 그림에서 이 전 두 가지의 모델에 비해 눈에 띄게 달라진 것을 보자면, 돋보기만으로 도청만 하는 것이 아니라 특정 message에 대한 암호문(ciphertext)을 요청할 수 있다는 점입니다. 공격자 A는 자신이 원하는 message를 선택해서 암호문을 알아낼 수 있습니다. 요청하는 횟수는 제한이 없어서 공격자가 원하는 만큼 선택한 평문(plaintext)들에 대해 암호문(ciphertext)을 알아낼 수 있는 것이 큰 특징입니다. 이때 security goal은 "ciphertext c가 주어졌을 때 공격자가 message m에 대한 정보를 알 수 없다면 안전하다" 입니다. 즉, 요청하지 않은 새로운 message m에 대한 ciphertext c가 어떤 message에서 왔는지 알 수 없어야 합니다.

CPA-attack 방법은 아래와 같습니다.

$\begin{aligned} Fi&x \;\;\;\; Scheme \;\mathrm{\Pi} \;\;\;\; Attacker \; A \\ De&fine \; a \; randomized \; exp't \; PrivCPA_{A, \Pi}(n): \\ 1.&\;\; k \leftarrow Gen(1^n) \\ 2.&\;\; A(1^n) \; interact \; with \; an \; encryption \; oracle \; Enc_k(\cdot), \\ & \; \; and \; then \; outputs \; m_0, m_1 \; of \; the \; same \; length \; A(1^n) \\ 3.&\;\; b \leftarrow \{0, 1\}, \;\; c \leftarrow Enc_k(m_b), \;\; give \; c \; to \; A \\ 4.&\;\; A \; can \; continue \; to \; interact \; with \; Enc_k(\cdot) \\ 5.&\;\; A \; outputs \; b'; \; A \; succeeds \; if \; b=b', \; and \; experiment \; evaluates \; to \; 1 \end{aligned}$

이때 공격자 $A$는 2번과 4번에서 encryption oracle과 interaction하는 과정에서 message에 대한 정보를 얻을 확률이 생깁니다. 공격자가 $b=b'$를 맞출, 즉 성공할 확률인 $PrivCPA_{A, \Pi}(n)$로 정의한 CPA-security는 아래와 같습니다.

4. Random encryption

하지만 위 방법만 보면 약간의 문제가 보입니다. 공격자 $A$가 성공할 확률이 $1/2 + \epsilon(n)$이 되어야 하는데, 공격자가 요청 작업 반복이 지속될수록 $A$의 성공 확률이 1에 가까워지게 됩니다. 가령, 공격자 $A$가 encryption oracle에 요청하여 $m_0, m_1$에 대한 암호화 결과값 $c_0=Enc_k(m_0)$과 $c_1=Enc_k(m_1)$을 얻었습니다. 공격자가 challenge에 응했을 때 받은 ciphertext c의 값이 $c_0$이나 $c_1$ 값과 같다면, $A$는 충분히 message가 $m_0$이나 $m_1$이라는 것을 알 수 있을 것입니다. 만약 encryption oracle에 요청을 $m_2, m_3,... , m_t, ...$까지 더 많은 message의 encryption 값을 계속한다면, 결국 성공 확률은 점점 1에 가까워질 것입니다.

따라서 동일한 메시지를 암호화하더라도, 서로 다른 결과값이 나와야 이러한 문제점을 해결할 수 있습니다. 즉, 암호화의 결과값이 결정된(determistic) 것이 아니라 랜덤(randomized) 결과값이 나와야 합니다.

1-2 Pseudorandom functions and block ciphers

동일한 메시지(message)에 대해 서로 다른 암호(ciphertext)가 나와야 한다면, 동일 값에 대해 매번 다른 함수를 사용하여 결과값도 다르게 출력하는 랜덤(random) 함수가 있어야 합니다.

1. Random function

위 함수는 0과 1로 이루어진 n-bit string의 집합에서 중복 순열로 0과 1로 이루어진 n-bit string을 매핑해주는 함수입니다. 함수의 매핑 테이블은 여러 개가 나올 수 있겠죠?
만약 3 bit string에 대한 매핑 테이플을 만든다고 합시다. 총 만들어질 수 있는 string의 개수는 $2^3=8$개입니다. 즉 n-bit string으로 만들 수 있는 전체 개수 $2^n$의 string이 모두 n-bit string $2^n$개로 매핑이 가능하므로, $Func_n$의 크기는 $(2^n)^{2^n}$입니다.

하지만 이렇게만 보면 이 함수는 중복되어 매핑된 값이 생길 수 있으므로 모든 매핑이 균일(uniform)하게 이루어져 있다고 볼 수 없습니다. 우리가 정의하고자 하는 random function은 uniform function을 말합니다. $Func_n$ 가 될 수 있는 함수들이 나올 확률이 동일한 함수를 random function의 자격이 된다고 봅니다.

2. Pseudorandom function (PRF)

Pseudorandom의 개념은 이전 포스팅에서도 다뤘기 때문에 익숙하실거라 생각이 듭니다. Pseudorandom이 random처럼 보이는 것이라면, Pseudorandom function은 random function처럼 보이는 것을 말합니다. Pseudorandom generater(PRG)를 봤을 땐 결과값이 되는 문자열이 uniform하게 뽑히는지에 대해 살펴봤다면, 이젠 그보다 더 큰 집합인 정의역과 치역이 uniform하게 뽑히는지를 더 집중하면 이해가 쉬울 것같습니다. 위에서 봤던 Random function이라면, 사용하는 함수가 fixed function이라고 볼 수 없습니다. 이용할 때마다 새로운 함수가 나와야하기 때문입니다. 하지만 일반적으로 우리가 생각하는 함수는 어떤 $x$에 대해 $y$가 고정되어 있으므로 fixed function이 대부분이었습니다. 이러한 관점에서 보면 random function을 머릿속에 그리기란 쉽지 않을 것입니다. 그래서 key를 도입한 keyed function으로 pseudorandom function을 살펴보려 합니다.

| Keyed functions

Pseudorandom function $F$는 아래와 같습니다.

$F$는 $\{0, 1\}^*$와 $\{0, 1\}^*$ 조합의 정의역 집합들을 가지고 있고 $\{0, 1\}^*$의 출력을 치역 집합으로 갖는 함수입니다. 보다 쉽게 정의하면 $F : K \; \times \; X \; → \; Y$과 동일합니다. 이 정의대로 해석하면 $F$는 $*$ bit짜리 key 조합들와 $*$ bit짜리 message 조합들에 대해 $*$ bit짜리 ciphertext 조합들이 나오는 함수입니다. $Y$는 $X$의 집합이 동일하더라도 $K$ 값에 따라 함수가 충분히 달라질 수 있기 때문에 이젠 random function의 개념에 조금 더 가까워진 것같습니다.
조금 전 살펴 본 random function에서 $x$와 $y$는 모두 $\{0, 1\}^n$에서 균등하게 뽑혀야 했습니다. 이 개념을 $F$에도 적용해보겠습니다. $k$와 $x$에 대한 함수 $F$를 $F_k(x) = F(k, x)$라고 합시다. 이 함수 $F(k, x)$는 $|k|=|x|$일 때만 정의되며, $|F(k,x)| = |k| = |x|$ 입니다. 즉 $*$의 길이는 모두 동일합니다.
$x$와 $y$에 대한 세팅을 마쳤으니, 이제 $k$도 살펴봐야겠죠? key $k$를 뽑아봅시다. $k$ 또한 동일하게 uniform한 조건 아래에서 뽑아야 합니다. 지난 시간 공부한 PRGs를 이용하면 key를 random한 것처럼 생성할 수 있을 것입니다.
오늘 배우고자 하는 PRF도 대상만 함수일 뿐이지 똑같습니다! $F$에서 $Y$를 함수들의 집합으로 생각해보세요. 우리가 key $k$를 $\{0, 1\}^n$ 중 uniform하게 뽑는 것처럼, 함수 $F$ 또한 $F_k : \{0, 1\}^n → \{0, 1\}^n$ 의 함수들 중 특정 $F_k$ uniform하게 뽑는 것입니다.

| Pseudorandom functions (PRFs) 정의

Keyed functions을 바탕으로 PRFs를 정의하겠습니다.

$F_k$는 완전하게 랜덤인 함수 $f$의 집합 $Func_n$과 구분하기 어려운 PRF 집합입니다. D는 공격자가 다항 시간동안 두 함수 중 어떤 함수가 랜덤인지 구분하는 테스트의 확률 분포입니다. 이때 각각의 집합에서 뽑은 두 함수는 다항 분포 D에서 완전히 랜덤하게 뽑은 것과 PRF로 뽑은 것을 구분하기 어렵습니다.

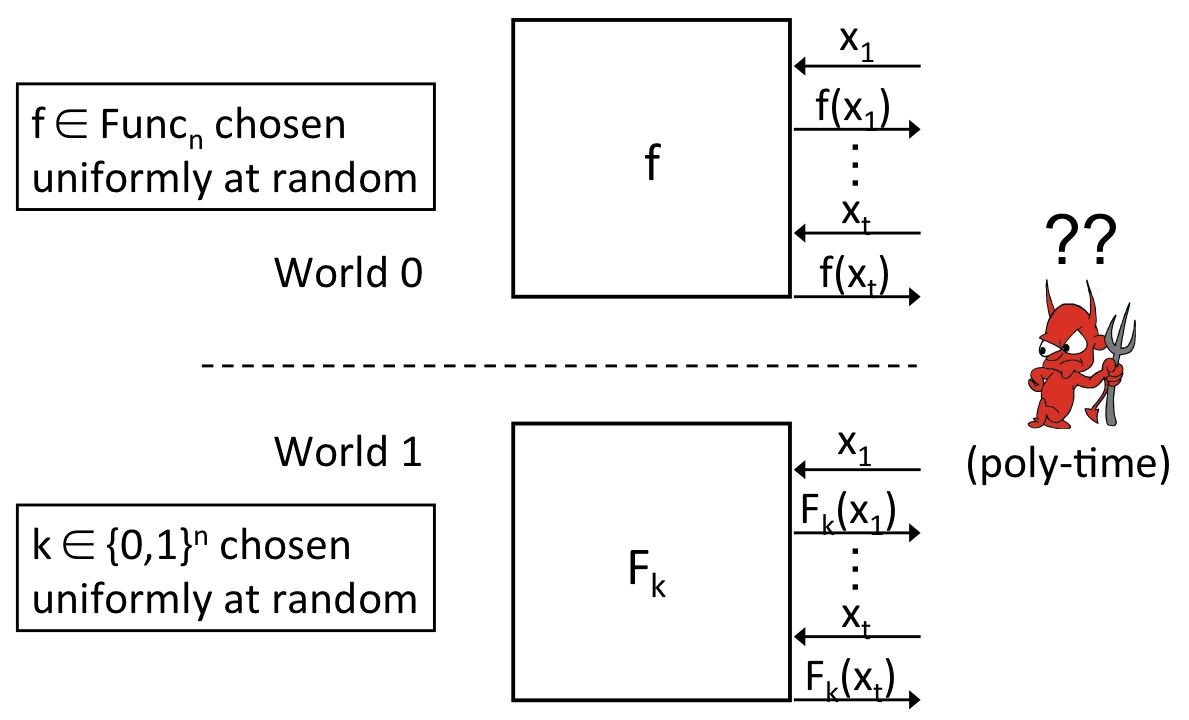
위 그림은 PRF의 정의를 보다 쉽게 설명하고 있습니다. 공격자는 완전히 랜덤한 $f \in Func_n$와 랜덤하게 뽑힌 key $k \in \{0, 1\}^n$에 대한 $F_k$로 생성된 두 함수로, 동일한 값 $\{x_1, x_2, x_3,...,x_t \}$에 대하여 함수값을 요청합니다. 요청은 공격자가 원하는 값을 원하는 만큼 요청할 수 있습니다. 이 요청 결과값을 확인하고 공격자는 어떤 함수에서 얻은 함수값이 실제 랜덤으로 생성된 것인지 알아 맞추는 테스트입니다.
한 가지 주의해야할 점은, $f$를 뽑은 $Func_n$이 랜덤할 뿐 $f$ 자체는 결정론적인(determistic) 함수입니다. $Func_n$의 아주 많은 $f$ 중 하나의 $f$를 뽑는다는 점에서 함수의 결정이 랜덤인 것이지, 뽑힌 함수 내의 정의역과 치역 간 관계가 랜덤인 것은 아닙니다.

3. PRFs vs PRGs

이쯤되면 PRFs와 PRGs의 차이가 궁금해지네요. PRFs와 PRGs의 관계에 대해 알아보겠습니다. PRGs는 PRFs로 환원이 가능합니다. PRFs를 생성할 수 있다면, PRGs도 쉽게 만들어낼 수 있습니다.
$F$를 PRF, $G$를 PRG라고 할 때 $G(k)$는 $F$로 정의할 수 있습니다.

위 정의에서 $F$로 환원한 $G$를 봅시다. $G$에 시드 $k$를 입력한 결과값으로 0,...,0에 대한 $F_k$와 0,...,1에 대한 $F_k$를 이은 값이 나옵니다. $F_k$는 $k$에 대하여 uniform하다고 볼 수 있는 함수이므로 그 함수의 결과값 또한 uniform하게 나올 것입니다. $F_k$ 입력값과 함수값이 n-bit라고 한다면, $G(k)$의 결과값은 n-bit 함수값 두 개를 이은 2n-bit 만큼의 출력에 매핑된 $G$ 결과값을 얻을 것입니다.

이번엔 새로운 예시를 가져왔습니다. 이번엔 $F$를 더 많이 이어보겠습니다. 만약 $G(k)$가 더 긴 key를 얻고 싶다면 $F_k$를 더 많이 이어 원하는 만큼의 길이 key를 생성할 수 있을 것입니다. 앞서 $F \; : \; K \times \; \{0,1\}^n \; → \; \{0,1\}^n$로 정의했고 $G \; : \; K \; → \; \{0,1\}^n$이므로, $F$의 함수값들을 연결하여 key의 길이 이상의 새로운 uniform한 값을 만들어 낸다면 PRGs의 기능과 동일한 기능을 하게끔 만들 수 있을테니까요. PRF는 uniform한 청크로 이어진 아주 긴 PRG 결과값의 부분으로 볼 수 있겠네요!

더불어 본 강의에서는 $F_k$에 대해 위와 같이 표현합니다. 수식적으로 이 공식이 완전히 맞는 건 아니지만, $F_k$의 특정 입력에 대한 결과값 테이블을 만든다고 가정하여 위 식에 접근해 봅시다. 이때 $F_k$로 만들어질 수 있는 모든 결과값은 위 수식처럼 $F_k$에 0,...0 부터 1,...,1까지 넣은 값들의 집합일 것입니다. 우변의 수식은 가능한 모든 입력을 $F_k$에 넣은 결과값의 나열이고, 이는 랜덤함수와 동일하게 랜덤하게 나올 가능성이 있는 모든 결과라는 의미에서 $F_k$의 function table이라고 볼 수 있습니다.

4. Pseudorandom permutations (PRP)

Pseudorandom permutation은 PRF의 개념에 일대일대응의 개념을 추가한 것입니다. 전단사함수(bijection function)라고도 하는데, 정의역과 치역의 모든 원소를 중복 없이 일대일로 대응하는 함수를 말합니다. 어떤 함수가 일대일대응이라는 건 그 함수의 역함수가 존재한다는 말과 같습니다. PRP도 PRF와 마찬가지로 정의부터 살펴보겠습니다.

쉽게 말해 완전히 랜덤한 순열과 구별할 수 없는 순열을 만들어주는 것을 PRP라고 합니다. PRF인 $F_k$가 주어진 $k$에 대하여 역수가 존재하고(일대일대응) 그 역수를 효율적으로 계산할 수 있다면 $F$를 pseudorandom permutation(PRP)라고 볼 수 있습니다.

5. Block ciphers

PRF와 PRP를 다룬 이유는 동일 값에 대해 매번 다른 함수를 이용하여 다른 결과값을 출력하기 위함이었습니다. 이를 사용한 암호화 방법이 Block cipher입니다.

| 특징

• Asymptotic 정의를 사용하지 않는다.
  Block cipher는 입력값과 출력값의 크기가 동일합니다. PRF의 개념적 수식으로 정의하면
  $F:\{0,1\}^n \times \{0,1\}^m → \{0,1\}^m$
  즉 n-bit 짜리 key에 대하여 입력과 출력이 m-bit로 고정되어 있습니다. 이렇게 특정 길이의 key와 입출력에만 정의되는 암호화 scheme이기 때문에 asymptotic definition이 아닌 concrete definition만을 사용합니다.

• 공격자가 $2^n$의 running time동안 $f \in Perm_m$를 완전히 랜덤한 순열과 구분할 수 없다면 안전하다고 본다.
  위에서 말하는 $n$은 PRP에서 사용되는 key의 길이를 말합니다. 그렇다면 n은 충분히 큰 수일 것입니다. Block cipher는 PRP에 대한 security의 기준을 공격자가 key에 대한 정보를 얻을 확률이 random permutation과 비교했을 때의 정도에 따라 판단합니다. 실제로 똑같은 PRP이지만 1-bit key에 대한 PRP와 128-bit key에 대한 PRP의 안전성은 다를 것이기 때문입니다.
  
  

6. AES

AES(Advanced encryption standard)는 대표적인 block cipher입니다. Block cipher는 블록과 key의 길이가 고정되어 사용된다고 했는데, 가장 흔히 사용되는 AES의 블록 길이는 128-bits로 고정되어 있습니다. key의 길이는 128, 192, 256-bits 중 채택하여 사용됩니다. 다른 block cipher도 물론 존재하지만, 본 강의와 포스팅에서는 AES만을 다루겠습니다.

2-1 CPA-secure encryption from PRFs/block ciphers

지난 강의에서는 pseudorandom function(PRF)과 pseudorandom permutation(PRP)를 집중적으로 살펴봤습니다. 사실 충분히 큰 n에 대해서는 random function과 random permutation은 구별하기 어렵습니다. 물론 일대일대응 여부에 대한 차이가 존재하지만, 결국 permutation도 function에 포함되기 때문입니다. 따라서 pseudorandom permutation과 pseudorandom function 또한 구별하기 힘듭니다. 즉 n이 충분히 크다면 PRP도 PRF라고 볼 수 있습니다. 그런 측면에서, block cipher 또한 하나의 PRF라고 볼 수 있습니다. 앞으로 PRF가 필요할 경우 block cipher를 이용하면 되겠죠.

1. CPA-secure encryption

다음 내용을 살펴보기 전에, 중간 점검 차 지금까지 배운 내용을 정리해보겠습니다. OTP의 한계 중 매번 다른 key를 사용해야 한다는 점을 극복하고자, 메시지를 여러 개 보냈을 때 안전한 scheme을 찾으려 했습니다. 그 일환으로 매핑이 서로 다른 function이 uniform하게 선택되는 random function을 보며, 이에 준하는 pseudorandom function(PRF)가 있다면 동일한 메시지라고 한들 서로 다른 결과값이 나오도록 만들 수 있을 것입니다. 그리고 이러한 scheme의 안전성을 확인하기 위해 single message secrecy이 아닌 여러 메시지에 대한 안전성을 확인하는 multiple message secrecy을 살펴보았고, 이보다 더 강력한 CPA secrecy까지 배워습니다. CPA-secure encryption을 다시 한 번 정의해봅시다.

| 정의

CPA-secure encryption은 다음과 같이 정의합니다.

• keyed function $F$ (permutation이 아니어도 됨)
• $Gen(1^n)$: 0과 1로 이루어진 n-bit uniform key 생성
• $Enc_k(m)$, for $|m| = |k|$:
  • 0과 1로 이루어진 n-bit uniform random r 선택
  • output ciphertext: $<r, F_k(r) \oplus m>$
• $Dec_k(<c_1,c_2>)$: $c_2 \oplus F_k(c_1)$

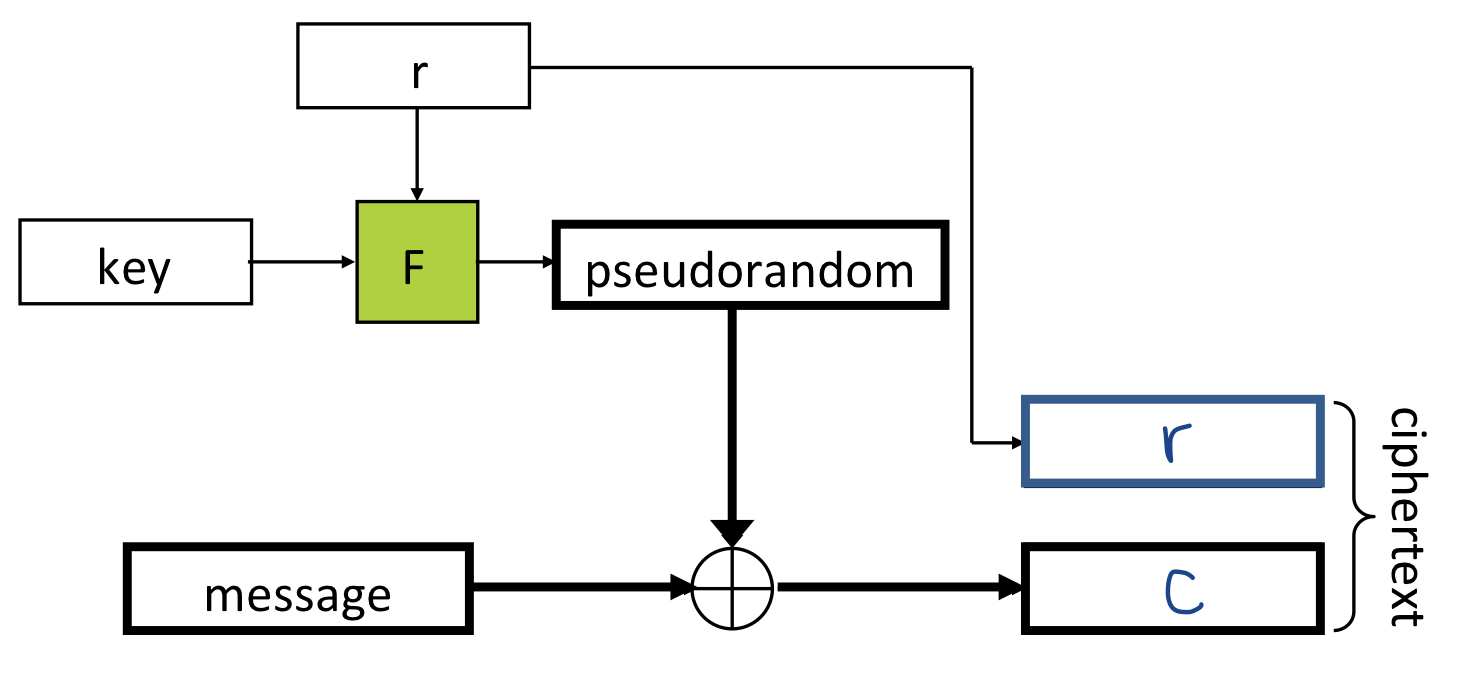
그림을 통해 더 쉽게 이해해봅시다. Decryption의 결과값은 $c1, c2$ 두 값입니다. $c1$은 같은 값을 넣어도 매번 바뀌는 랜덤 요소이고, 두 번째 값 또한 그 랜덤 요소에 영향을 받아 생성됩니다.

이 암호화 scheme이 OTP의 한계를 극복할 수 있을까요? 우선 key는 PRGs를 사용함으로써 메시지의 길이와 같거나 길게 만들어주었습니다. Key보다 더 긴 메시지를 암호화하는 데 사용할 수 있는 것입니다. 동일한 key를 두 번 사용할 수 있을까요? CPA-secure encryption은 동일한 key로 여러 메시지를 안전하게 암호화할 수 있습니다. 그런 면에서 OTP보다 훨씬 좋은 scheme이라고 볼 수 있죠.

| 증명

CPA-secure을 만족하는지 여부를 아래와 같이 증명할 수 있습니다. 지난 주에 다루었던 증명과 마찬가지로 이 또한 reduction 방식으로 증명이 가능합니다. Pseudo-OTP처럼 CPA-secure encryption의 security를 직접적으로 증명하는 것은 어렵기 때문에, $D$라는 알고리즘이 있다고 가정하고 문제를 접근합니다. 이때, pseudorandom과 truly random의 구별을 할 수 없다는 것을 이용해 증명을 하는데 자세한 내용은 다음과 같습니다.

• Theorem : $F$가 PRF라면, 이 sheme $\pi$는 CPA-secure이다.

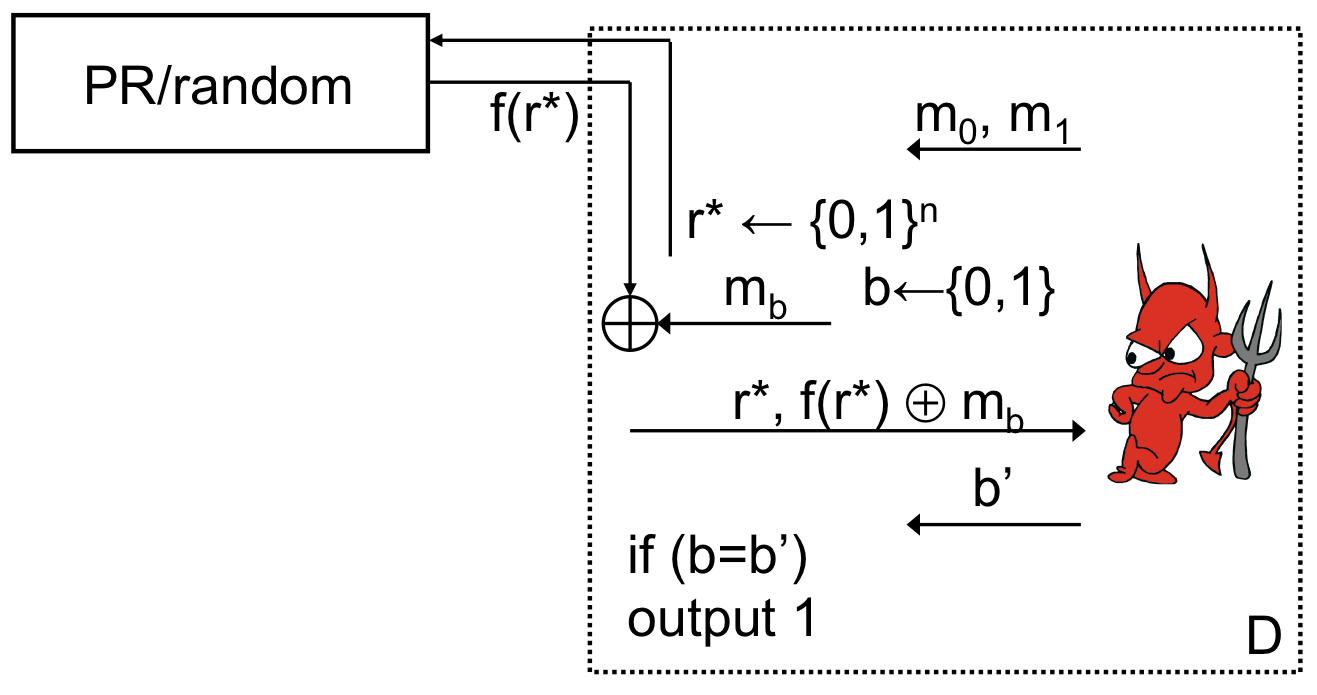
$D$는 임의의 uniform한 값인 $r$을 뽑아 이 값을 PR/random oracle에 쿼리하여 $f(r)$을 반환해 받는 알고리즘입니다. $D$로 받은 $f(r)$을 이용하여 CPA-encryption을 진행하고, 그 결과값에 대해 공격자가 $m0, m1$ 두 메시지 중 어떤 메시지에 대한 결과값인지를 알아맞추는 공격 모델입니다.

공격자가 이를 맞출 확률인 $\mu(n)$은 다음과 같이 정의합니다.

위 수식에서 $f$가 uniform하게 뽑힌 함수라면, 다음 두 가지 경우의 수가 존재할 수 있습니다.

• $r^*$가 반복적으로 쿼리될 때
• $r^*$가 반복되지 않을 때

이 두 경우의 수에서 각각 발생할 성공확률을 더해주면 $f(\cdot)$에 대한 총 성공확률이 될 것입니다.

이때, $Pr[Repeat]$은 n-bit의 random한 값을 뽑는다면, 랜덤한 n개의 bit들을 맞출 확률 $1/2^n$을 $q(n)$번 반복한 것과 같으므로, $q(n)/2^n$보다 작거나 같다고 볼 수 있습니다.

하지만 여기서 F는 pseudorandom이기 때문에 위 식을 다음과 같이 수정하면, 아래 식이 성립하여 secure함을 보일 수 있습니다.

2-2 Modes of encryption

앞서 block cipher나 PRF를 기반으로 한 CPA-secure encryption scheme을 살펴보았습니다. 암호화의 결과값으로 $Enc_k(m)=(r, F_k(r) \oplus m)$이 출력되어, 하나의 plaintext block을 입력으로 넣었을 때 두 block의 ciphertext가 나오는 형태입니다. CPA-secure을 보장한다는 점과 동일한 key를 여러 번 사용해도 된다는 점에서 좋은 이점을 가지고 있으나, 이 sheme은 오직 n bit에 대해서만 암호화를 할 수 있습니다. 그리고 random r을 $c1$으로 출력해야하기 때문에 ciphertext가 plaintext의 길이의 두 배가 되어 비효율적입니다. 이번 강의에서는 여러 길이의 메시지에 대해 암호화가 가능하면서도 ciphertext의 길이가 커지지 않는 더 효율적인 암호화 방식을 알아보겠습니다.

1. What is Modes of operation

Stream cipher에 대해서도 synchronized, unsynchronized 두 가지의 운영 모드가 있지만, 해당 강의에서는 block cipher에 대해서만 운영 모드를 살펴보겠습니다. Block cipher는 n-bit plaintext에 대하여 n-bit ciphertext로 암호화하는 방식인데, plaintext를 얼마만큼의 블록으로 나누고 어떠한 방식으로 암호화하는지에 따라 운영 모드가 다양합니다.

2. CTR mode

| 정의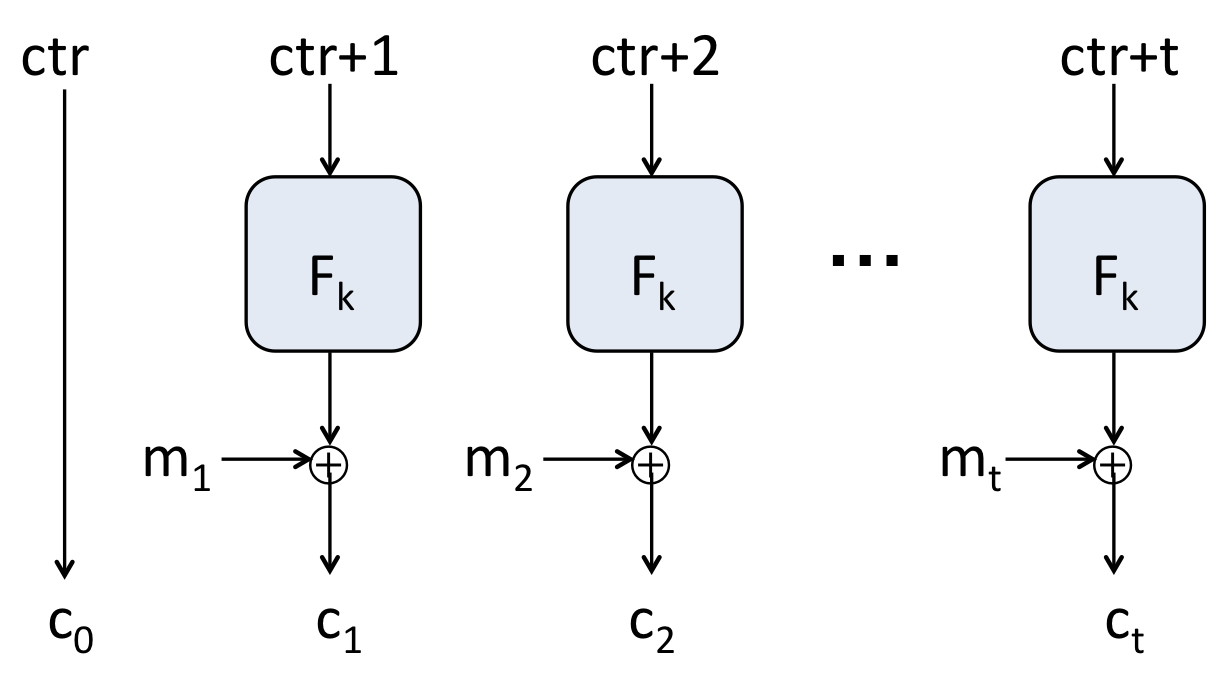

CTR mode는 블록을 총 $t$개로 나누어, n-bit 문자열 counter에 대해 index를 하나씩 더하여 PRF를 취하는 방식입니다. 정의하면 아래와 같습니다.

$Enc_k(m_1, .., m_t)$

• choose $ctr \leftarrow \{0,1\}^n$, set $c_0 = ctr$
• $For \; i=1 \; to \; t$:
  • $c_i = m_i \oplus F_k(ctr + i)$
• output: $c_0, c_1, .., c_t$

| 증명

$F$가 pseudorandom function이면, CTR mode는 CPA-secure 합니다.
길이가 $t$인 메시지 블록이 있다고 가정할 때, $i$번째 메시지 블록을 암호화하기 위해 사용된 함수 $F_k(ctr_i+1),...,F_k(ctr_i+t)$의 시퀀스는 가정에 의해 각각 pseudorandom 입니다. 이때 counter의 값은 전부 다르므로 counter에 대하여 $F_k$를 거쳐 나온 ciphertext들은 서로에게 영향을 받지 않은 독립적인 성질을 가집니다. 따라서 출력되는 값이 모두 다르기 때문에 CTR mode를 사용한 encryption은 CPA-secure합니다.

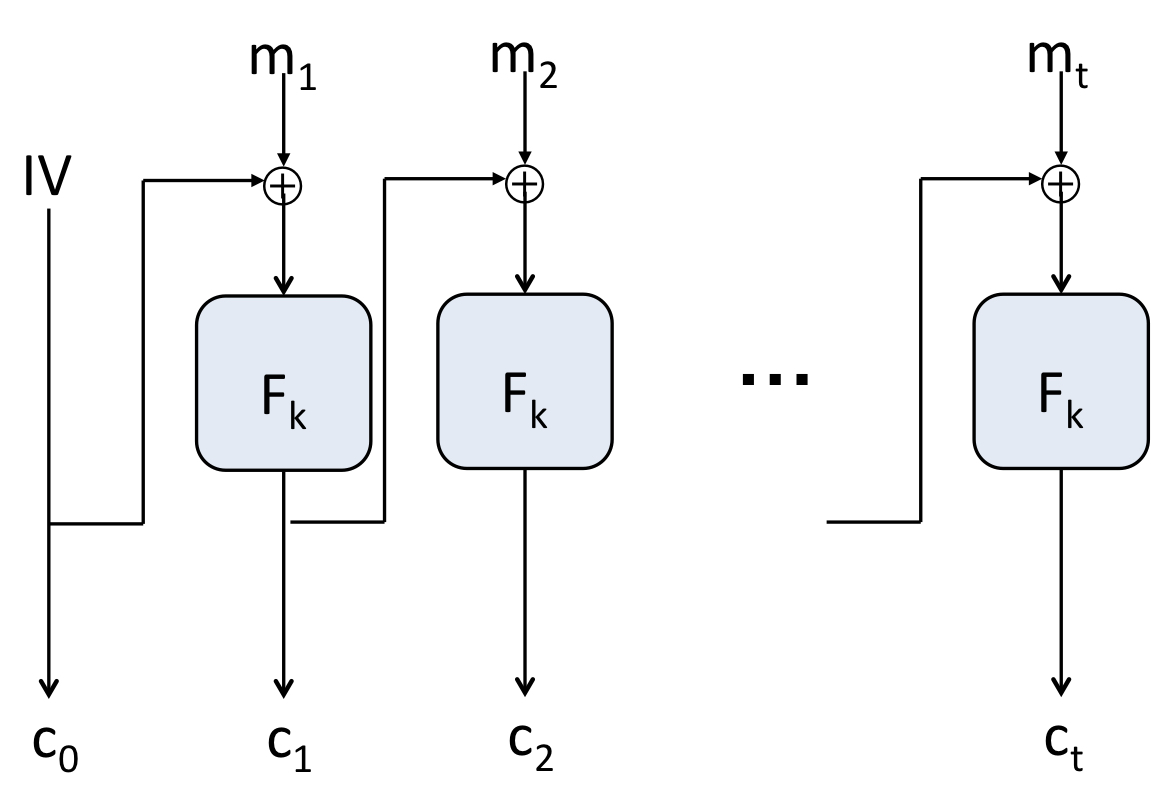
3. CBC mode

| 정의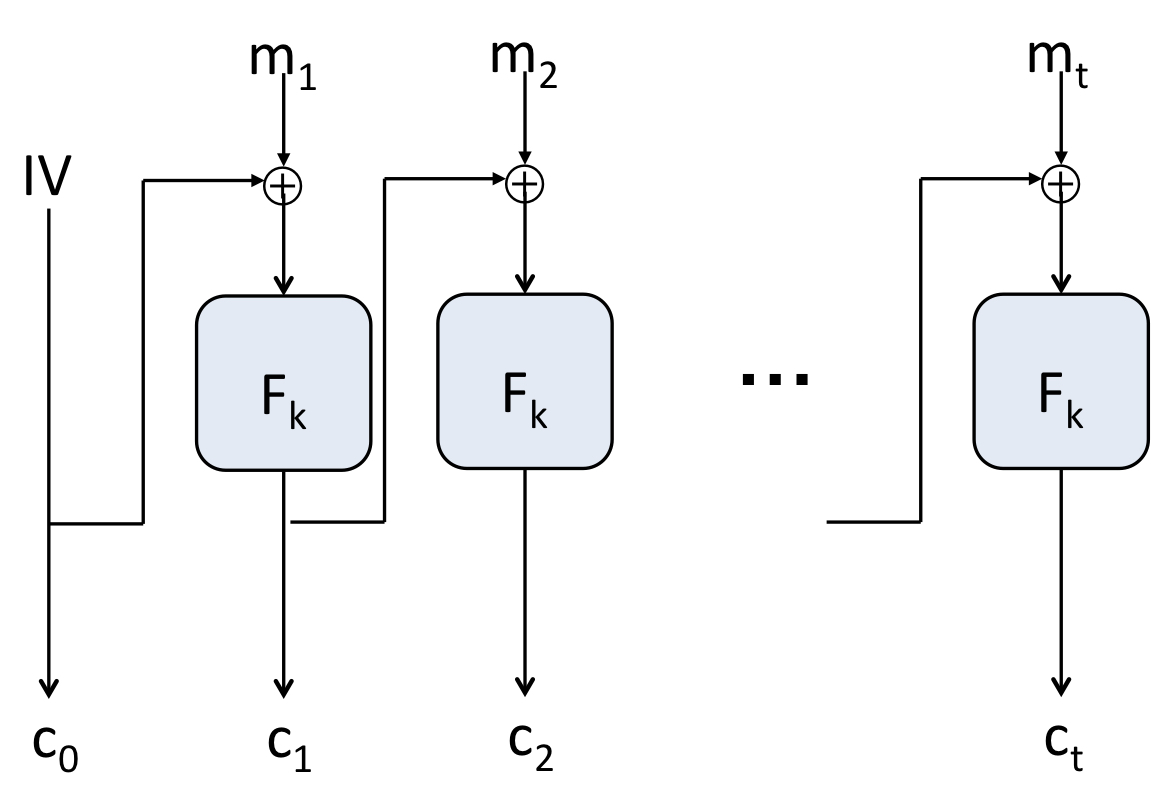

CBC mode는 각각의 블록이 이전 블록값과 XOR되어 PRF를 취하는 block cipher 방식입니다. 정의하면 아래와 같습니다.

$Enc_k(m_1, .., m_t)$

• choose random $c_0 \leftarrow \{0,1\}^n$ (also called the IV)
• $For \; i=1 \; to \; t$:
  • $c_i = F_k(m_i \oplus C_{i-1})$
• output: $c_0, c_1, .., c_t$

CBC 모드의 특징을 말씀드리겠습니다. CTR모드는 decryption을 취할 때 독립적인 결과들을 모아 ciphertext를 만든 것의 반대과정을 거치면 되었지만, CBC 모드같은 경우, 이전 블록이 뒤 블록에 영향을 미칩니다. 그래서 $F_k^{-1}$를 해야 합니다. 역함수가 있다면 일대일대응이라고 배웠었죠. 따라서 CBC 모드에 사용되는 $F$는 PRP여야 합니다.

| 증명

$F$가 pseudorandom function이면, CBC mode는 CPA-secure 합니다. (강의에서는 CTR mode보다 증명방식이 복잡하지만 그래도 증명 가능하다고만 이야기하고 넘어갔습니다....)

4. ECB mode

| 정의와 한계

ECB mode는 $Enc_k(m_1, ...,m_t)=F_k(m_1),...,F_k(m_t)$ 의 수식에서도 볼 수 있듯이, 각 블록을 동일한 $F_k$를 사용하여 암호화하는 방식입니다. 각 $F_k$는 determistic한 함수이기 때문에 동일한 입력값을 넣으면 동일한 결과값이 나올 것입니다. 이러한 암호화 방식은 한계를 가져옵니다.

만약 $m_i$와 $m_j$ $(i\;!=j)$가 동일하다면 같은 암호화 결과값이 나올 것입니다. 위 그림에서의 결과도 마찬가지로, 동일한 색깔에 대해 동일한 값이 출력되어 충분히 plaintext를 도출할 수 있으므로 이는 CPA-secure에 성립하지 않습니다.

3-1 Stronger notions of security: CCA-security

지금까지 다룬 공격 모델은 수동적이고 도청만 가능한 공격자였습니다. 이번엔 조금 더 강력한 공격모델을 살펴보려고 합니다.

두 당사자 Alice와 Bob의 ciphertext $c$를 가로채서 새로운 ciphtertext $c'$를 전송할 수 있는 모델, 그리고 송신자를 사칭하는 모델을 살펴보고자 합니다.

1. Malleability

중간에 전송되는 ciphertext를 변경하여 원래 plaintext에 예측가능한 변화를 줄 수 있는 것을 malleable이라고 합니다. 이게 현실적으로 가능한가에 대해 의문을 가질 수 있지만, 실제로 많은 곳에서 malleability를 지닌 공격이 일어나고 있습니다. 가령, 이메일과 같은 경우 원래 보내려는 이메일 정보를 가로채 새로운 내용의 이메일을 보낼 수도 있고, 다른 사람의 계좌번호와 비밀번호를 가로채 은행에 입금을 요구하는 것도 모두 malleability를 지닌 공격 방법입니다.

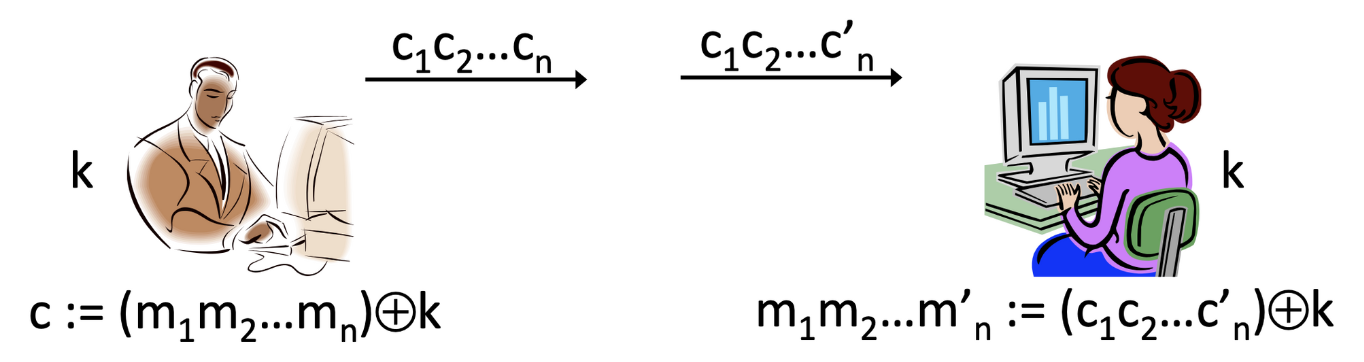
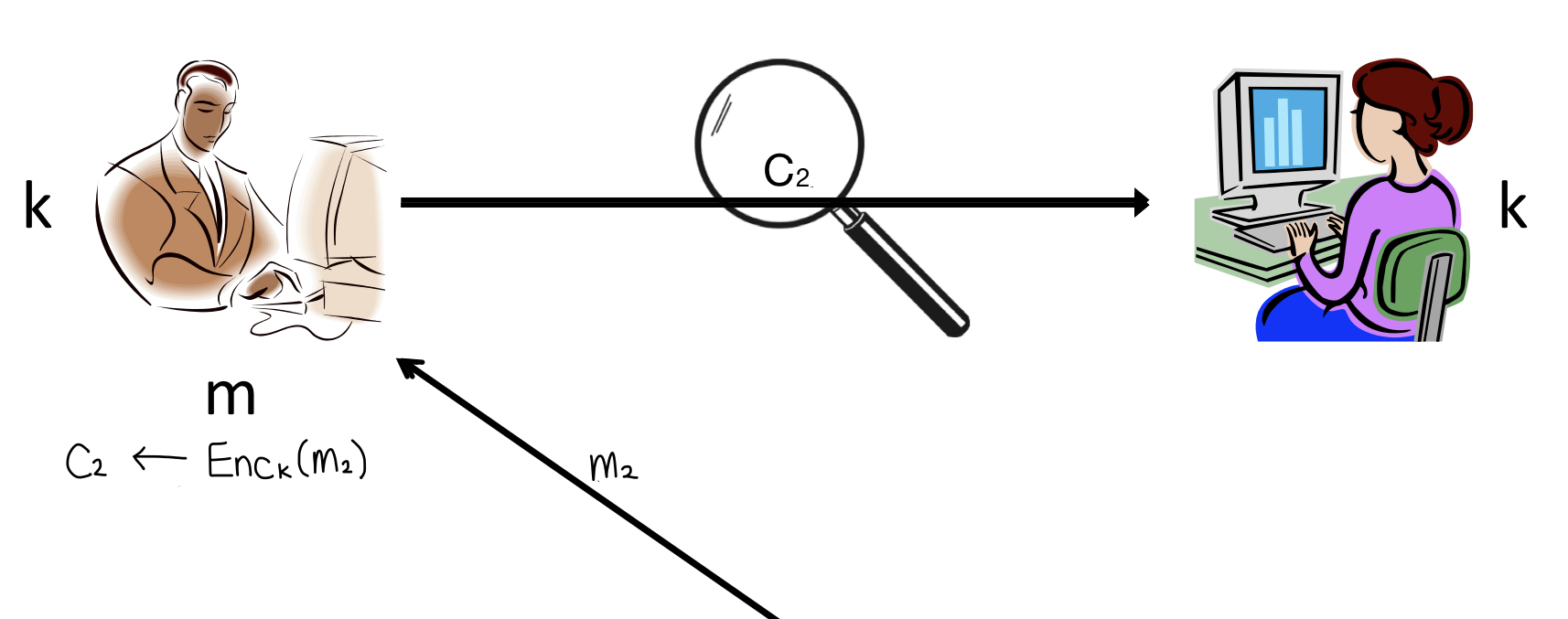
위 그림에서는 다른 cipertext는 그대로 둔 채 맨 마지막 메시지 $m_n$의 암호문인 $c_n$을 $c'_n$으로 바꿨습니다. 수신자가 이 잘못된 ciphertext를 복호화하면 원래 평문의 정보와 다른 정보를 받을 수 밖에 없겠죠. 이러한 경우 이 scheme은 malleable하다고 부릅니다.
사실 지금까지 우리가 배운 모든 scheme들은 malleability에 노출되기에 치명적입니다. OTP(one time pad), block cipher 모두 key에 대해 정보를 알고 있는 CCA가 이루어질 경우 새로운 암호문을 생성하는 것은 쉬운 일일테니까요.

OTP(one time pad)를 perfect secrecy를 만족하는 개념으로 배웠던 입장으로 굉장히 당황스러운 공격입니다.. 이를 대비한 scheme들은 추후에 다뤄보겠습니다.

지금까지 통신 채널에서 새로운 암호문을 만들어내는 모델을 봤다면, 이제 송신자를 사칭하는 모델을 살펴보겠습니다.

위 공격은 송신자가 그 어떤 ciphertext를 보내지 않아도 공격자의 마음대로 이루어질 수 있습니다. ciphertext를 보내 그에 대한 message를 알게 되기 때문에 치명적인 공격방식입니다.

2. Chosen-ciphertext attacks

위에서 다룬 공격을 정의해보겠습니다. CCA(Chosen-ciphertext attacks)는 공격자 $A$가 자신의 goal에 해당하는 암호문의 평문에 대해선 알 수 없지만, 그 외 자신이 원하는 메시지에 대해 암호화된 값과 복호화된 값을 알 수 있습니다. 즉, 어떤 메시지 $t$에 대하여 그 $t$를 encryption 알고리즘에 넣었을 때 나오는 값과 decryption 알고리즘에 넣었을 때 나오는 값을 알 수 있습니다. 공격자의 레벨이 CPA보다 더욱 높다고 볼 수 있죠.

3. CCA-security

CCA-security한 암호화 scheme을 정의하기 위해 아래와 같이 공격을 정의하여 공격자 $A$의 성공확률을 알아보려고 합니다.

$\begin{aligned} &Scheme: \mathrm{\Pi} \;\;\;\; Attacker: A \\ D&efine \; a \; randomized \; exp't \; PrivCCA_{A, \Pi}(n): \\ 1&.\;\; k \leftarrow Gen(1^n) \\ 2&.1.\;\; A(1^n) \; interact \; with \; an \; encryption \; oracle \; Enc_k(\cdot) , \\\;&and \; a \; decryption \; oracle \; Dec_k(\cdot)\\ 2&.2.\;\; m_0, m_1 \; of \; the \; same \; length\\ 3&.\;\; b \leftarrow \{0, 1\}, \;\; c \leftarrow Enc_k(m_b), \;\; give \; c \; to \; A \\ 4&.\;\; A \; can \; interact \; with \; Enc_k(\cdot), \; Dec_k(\cdot), \; but \; not \; request \; decryption \; of \; c \\ 5&.\;\; A \; outputs \; b'; \; A \; succeeds \; if \; b=b', \; \\ &and \; experiment \; evaluates \; to \; 1 \; in \; this \; case\\ \end{aligned}$

2.1번과 4번 부분은 공격자가 encryption oracle 및 decryption oracle과 소통하여 결과값을 얻어내는 부분입니다. 여기서 공격자는 자신이 원하는 평문에 대한 암호문을 얻어낼 수 있으며, 자신이 원하는 암호문에 대한 평문도 얻어낼 수 있습니다. 공격자 $A$가 $b=b'$를 맞출 확률인 $PrivCCA_{A, \Pi}(n)$에 대하여 CCA-security는 아래와 같이 정의합니다.

4. Chosen-ciphertext attacks and malleability

어떤 scheme이 malleable 하다면, CCA-secure 하지 않습니다. 즉, CCA-security는 non-malleability 특성을 함께 가지고 있습니다.

3-2 Padding-oracle attacks

현실에서 CCA(chosen-cipher attack)의 대표적인 예시가 Padding-oracle attacks입니다. 어떤 공격방식인지 살펴보도록 하겠습니다. Padding-oracle attack이 대표적으로 사용되는 운영 모드가 CBC mode 입니다.

CBC 모드에서는 random 벡터 $IV$를 뽑아, 이 전 블록의 결과값을 메시지와 XOR하여 PRP를 취했습니다. Block cipher는 입력과 출력의 결과값의 길이가 n-bit로 고정된다고 이야기했지만, 실제로 사용될 땐 동일한 비트에 맞추기가 쉽지 않습니다. 그래서 n-bit가 아니어도 해당 비트에 맞게 맞추기 위해 padding을 이용합니다.

1. Arbitrary-length messages?

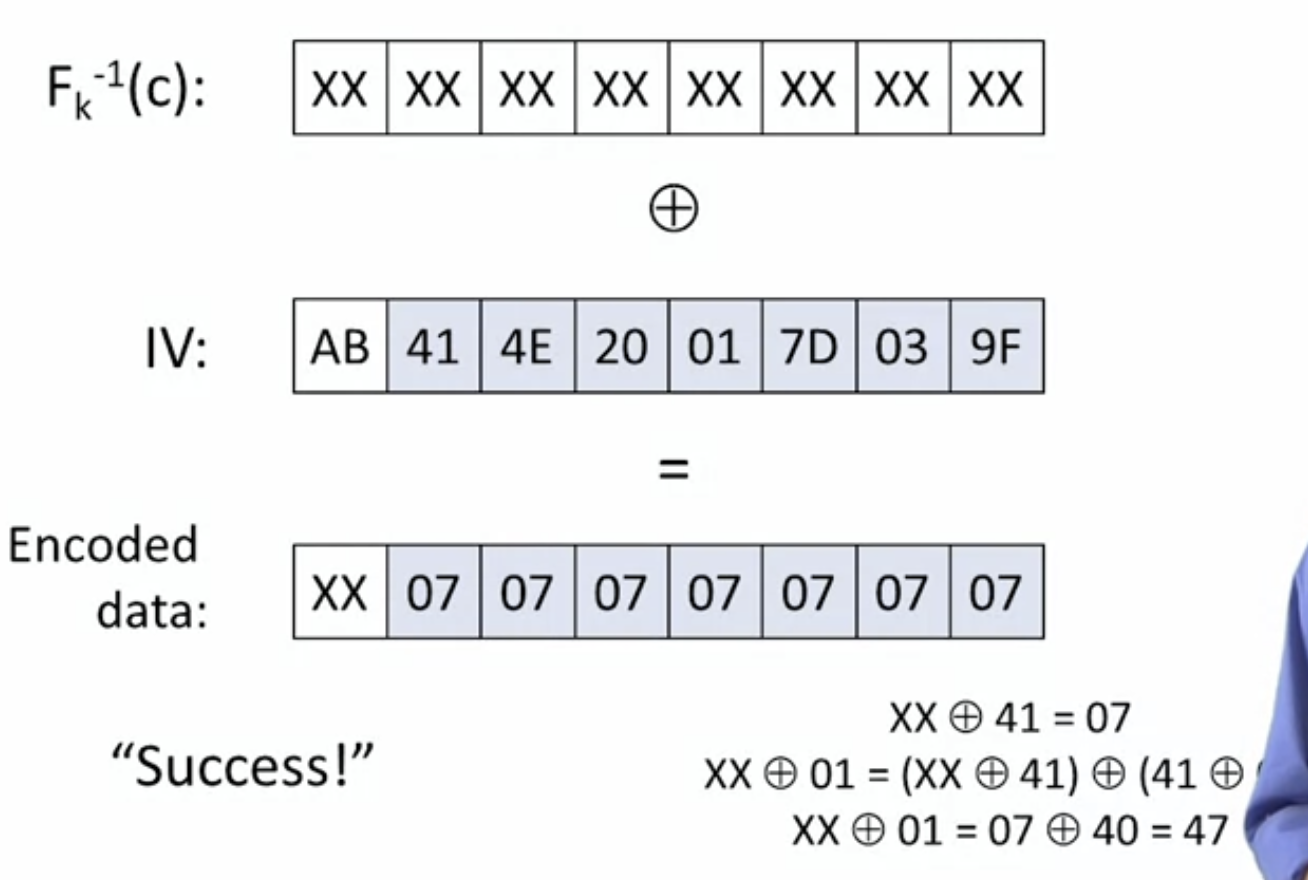
임의의 메시지 길이에 대해서는 PKCS #5 encoding방식으로 padding을 붙입니다. 어떤 L 만큼의 블록 길이에 대하여 b를 padding해 붙여야 하는 byte 값이라고 할 때, b를 b번 붙이는 방식입니다. 가령, 3 byte의 패딩이 필요하다면, 0x030303처럼 세 번 붙여 패딩을 붙여줍니다.

2. Padding oracles

Padding oracle attack은 decryption을 하는 과정에서 발생합니다. CBC-mode로 decryption을 진행할 때, 위의 인코딩 방식대로 패딩을 붙인다고 가정합시다.

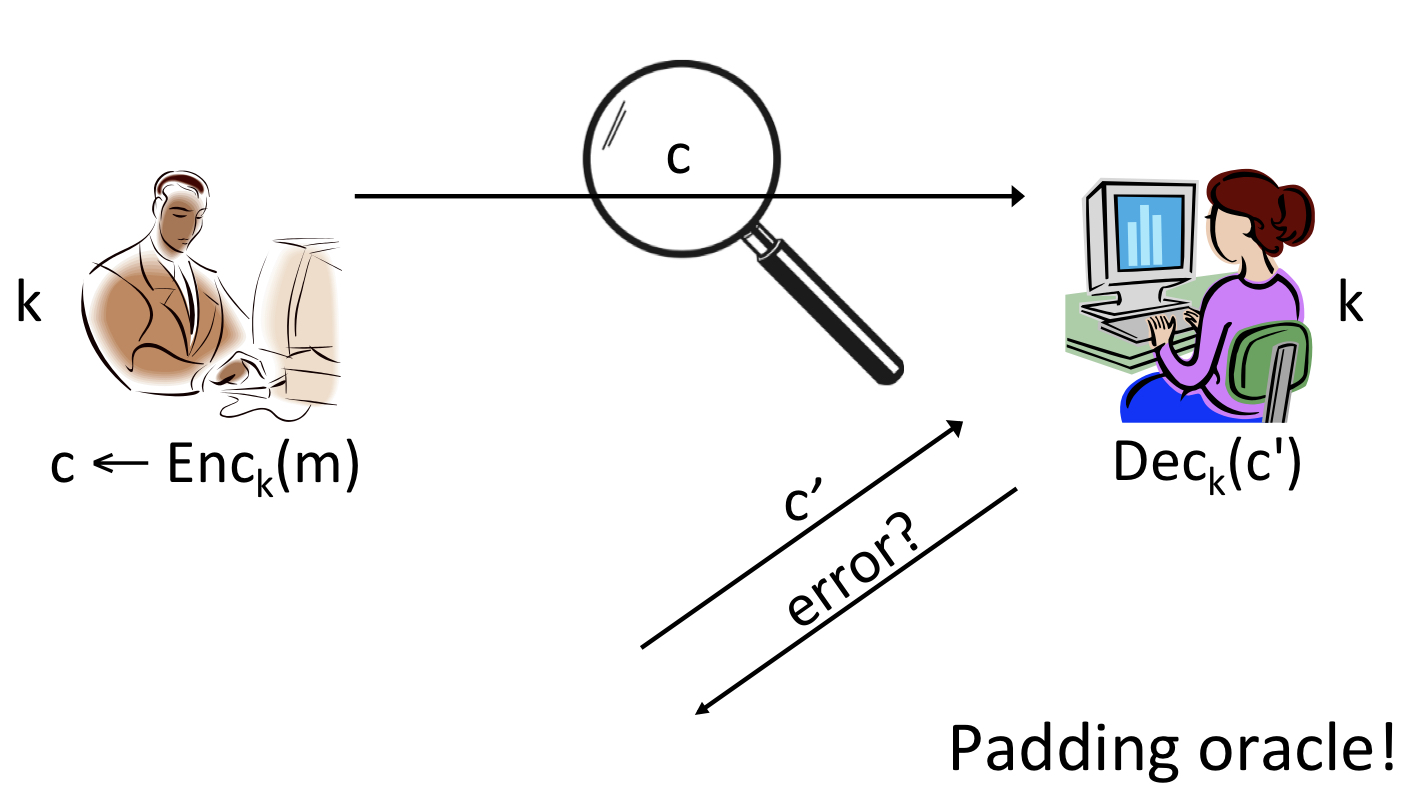
CBC-mode에서는 IV값이 있습니다. 2개의 block으로 이루어진 ciphertext는 IV와 c로 이루어져 있을 것입니다. 이때 이 IV의 끝 부분부터 bit 단위로 수정해 나가면서 padding 값을 찾습니다. 만약 padding 값을 찾지 못하고 있다면 서버에선 padding에 대한 error를 주지만, padding 값을 찾게 되면 서버에선 해당 부분을 padding으로 인식해 데이터를 주게 됩니다. 우리는 이 데이터를 통해 복호화된 평문을 알아낼 수 있습니다.