[Cryptography(암호학)] 1주차-Introduction to Classical Cryptography

본 포스팅은 Coursera | Cryptography - Jonathan Katz 강의를 수강하며 정리했습니다.

1-1,2 Introduction

고전적인 암호학의 정의는 말그대로 '암호'입니다. 두 당사자(Alice & Bob) 사이의 비밀을 보장하는 것에 초점을 맞춰, 공유 키(key)로 보내고자 하는 메시지를 암호화, 복호화 가능하도록 만드는 것이 목표였습니다. 두 당사자 간 공유된 키는 둘만 알고 다른 사람들에게는 비밀이라 하여, Private-key encryption이라고 부릅니다.

1. Private-key encryption

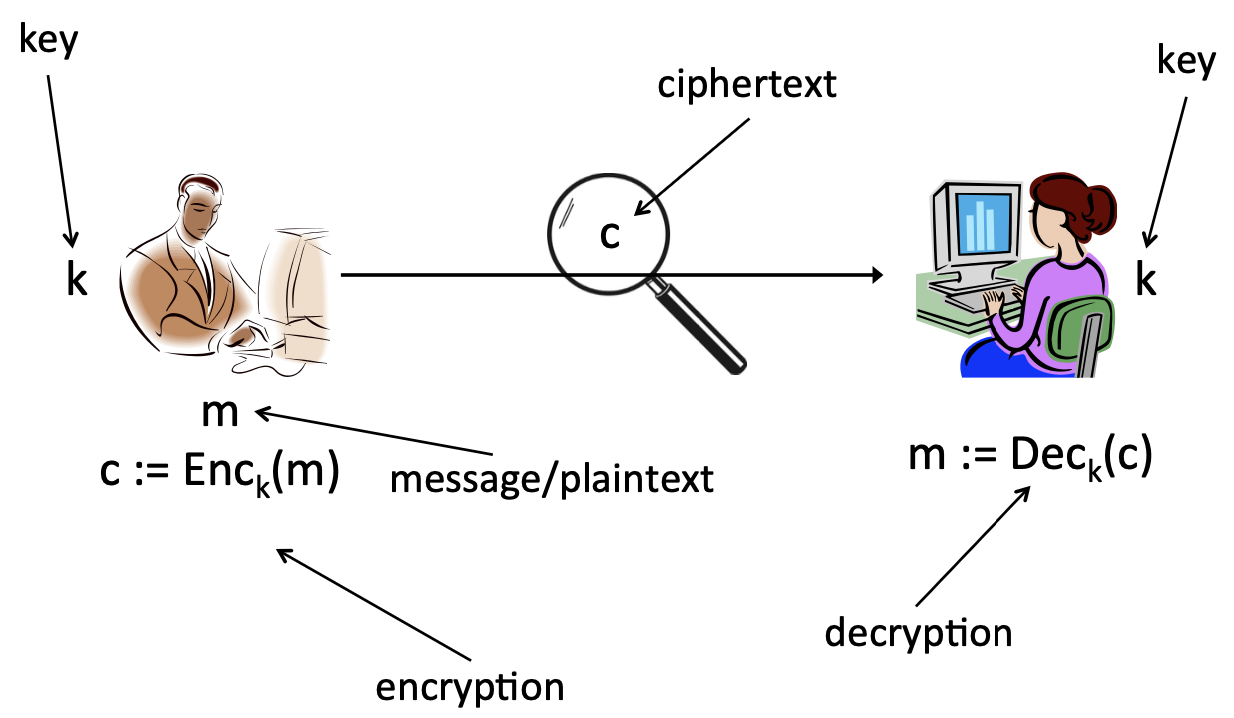Private-key encryption을 간단하게 그림으로 표현하면 위와 같습니다. Alice가 Bob은 key k를 공유하고 있습니다. Message/plaintext m을 k를 이용하여 암호화(encryption) 된 ciphertext c를 만들 수 있습니다. 한편, 이렇게 만들어진 c는 다시 k를 통해 본래의 m으로 복호화(decryption)됩니다.

이때 세 가지의 알고리즘이 사용됩니다.

• $Gen$: key k를 만들기 위한 key generator
• $Enc$: key k와 message m을 이용해 cipher text c를 만들어내는 encryption algorithm
• $Dec$: key k와 cipher text c를 이용해 message m을 복호화 하는 decryption algorithm

여기서 주목할 점은 $Enc$ 알고리즘과 $Dec$ 알고리즘의 정의 방식입니다.

$Enc$ 알고리즘은 정의를 ←로 표기했습니다. 이는 암호화 알고리즘의 출력이 랜덤하게 나올 수 있다, 즉 동일한 입력을 두 번 실행했을 때 서로 다른 결과값이 출력될 수 있다는 의미입니다. 한편 := 표기는 어떤 입력값을 넣었을 때 결과값이 결정론적으로 매칭됨을 의미합니다.
이 두 정의를 충족시키기 위해 아래 가정을 암호학의 기본 전제조건으로 두겠습니다.

2. The shift cipher

| 방법

shift cipher는 영어 알파벳으로 이루어진 문장에서 사용 가능합니다. 영어로 된 text에서 key k에 대해 k의 알파벳 순서만큼 text를 이동시켜 암호화하는 방법입니다.
방법을 더 자세히 살펴보겠습니다. 글자를 알파벳 순서대로 0부터 인덱스를 매겨 숫자로 바꿔보면 다음과 같습니다.

알파벳 'c'가 k가 될 경우, C=2 이므로, plaintext에 있는 알파벳 순서보다 두 칸 다음에 위치한 알파벳으로 암호화하면 됩니다. 예를 들어 'lalayun'이라는 m를 암호화하면 'ncncawp'가 되겠죠?

| 계산

알파벳은 총 26자로 이루어져 있기 때문에 모듈러 연산을 통해 쉽게 계산 가능합니다.

• $M$ = {English string 집합}
• $Gen$ = uniform한 확률로 k 선택 ($k \in \{0, 1, .., 25\}$)
• $Enc_{k}(m1 ... mt)$: $c_{i} = [m_{i} + k \,\bmod\, 26]$
• $Dec_{k}(c1 ... ct)$: $m_{i} = [c_{i} - k \,\bmod\, 26]$

| 안전성 (No!)

1. shift cipher에서 k의 집합 $K$의 원소 개수는 총 26개이므로, 최대 26번만 brute force를 진행하면 모든 경우를 다 찾아낼 수 있습니다.
2. cipher text가 충분히 길다면, 말이 되는 문장을 만드는 k는 단 하나로 정해질 것입니다.

★ Kerckhoffs’s principle

shift cipher에서는 key의 집합 원소의 개수가 작아 아무리 랜덤으로 key를 뽑는다고 하더라도 안전하지 않았습니다. 이처럼 key의 비밀성은 매우 중요합니다. 우리는 이런 암호화 원칙을 케르크호프스 원칙을 통해 확인할 수 있습니다.

• 암호화는 알고리즘의 안전성보다 key의 비밀성에 좌우되어야 한다.
  Key가 밝혀지지 않는 이상, 암호화 알고리즘이 공개되어도 키만 잘 지키면 안전한 암호 체계를 만들어야 한다. 즉, 공격자가 어떤 encryption 알고리즘을 사용했는지 알고 있더라도 key를 알지 못하면 공격하기가 어려워야 한다.

key에 대한 보안을 유지하는 것이 암호화 알고리즘의 보안을 유지하는 것보다 쉽습니다. 암호화 알고리즘이 밝혀질 경우, 알고리즘 자체를 변경하는 것보다 key를 바꾸는 것이 훨씬 효율적일 것입니다. 따라서 key의 비밀성을 유지하기 위해 충분한 key space를 확보하는 것이 중요합니다.

3. The Vigenère cipher

| 방법

shift cipher는 key가 알파벳 char 하나였다면, Vigenère cipher에서는 문자열이 key가 됩니다. 문자열을 이루는 각각의 알파벳 순서만큼 동일 위치에 있는 plaintext의 위치를 이동시켜 암호화하는 방법입니다. 예시는 아래와 같습니다.

| 안전성 (X)

Vigenère cipher의 key space는 $26^{len(string)}$이기 때문에 꽤나 큰 key 범위를 가지고 있어 안전하다고 여겨져 왔습니다. 하지만 큰 key space에도 불구하고 Vigenère cipher는 안전하지 않습니다.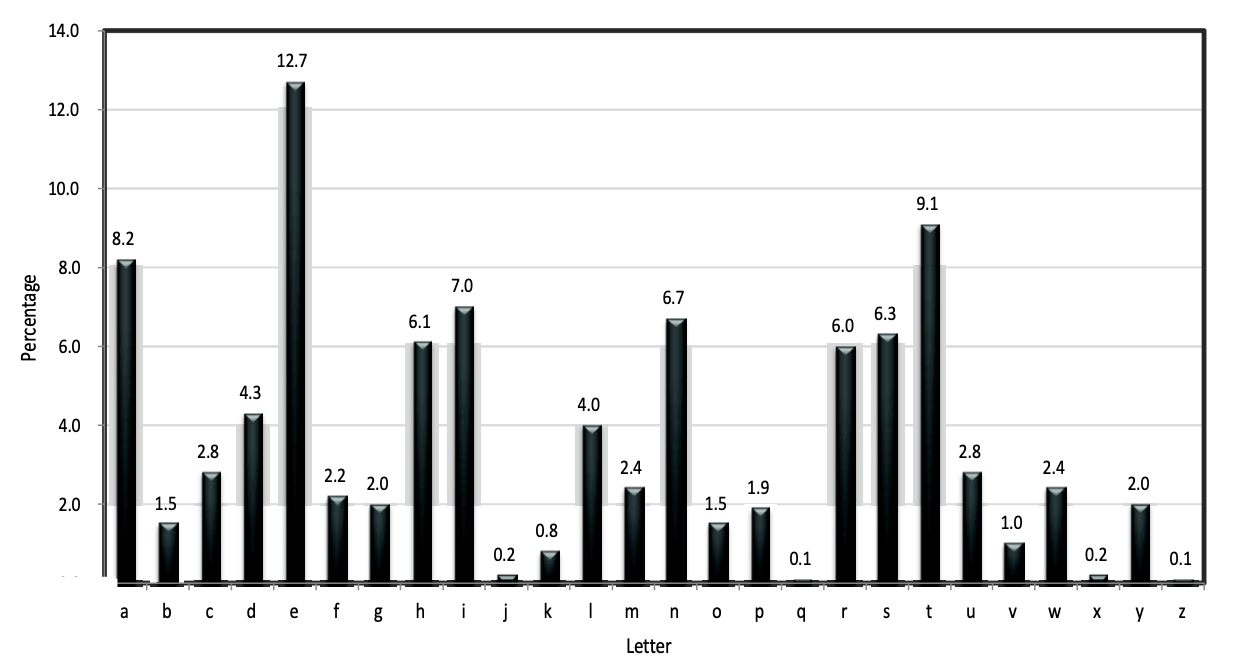
위 그래프는 알파벳 별 빈도수를 나타냅니다. 그래프를 보면 알파벳 e, a, t가 압도적으로 많은 빈도로 등장함을 알 수 있습니다. Vigenère cipher는 key의 길이만큼 key에 규칙성이 생깁니다. 이 길이를 t라고 할 때, (t+i)번 째마다 반복되는 문자열에 대해 빈도수 공격으로 충분히 ciphertext를 뚫을 수 있습니다.

1-3 Hex and ASCII

해당 lesson에서는 16진법과 ASCII 코드의 문자 환산법에 대해 다루고 있습니다. 아래 사진으로 대체하겠습니다.

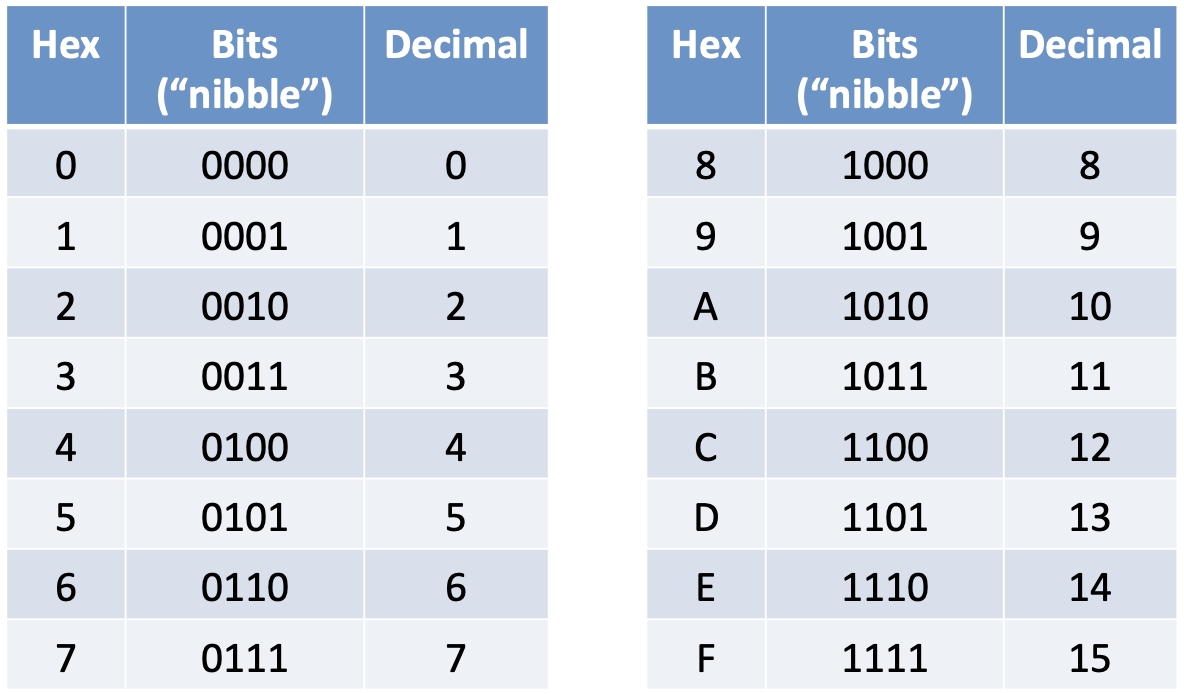
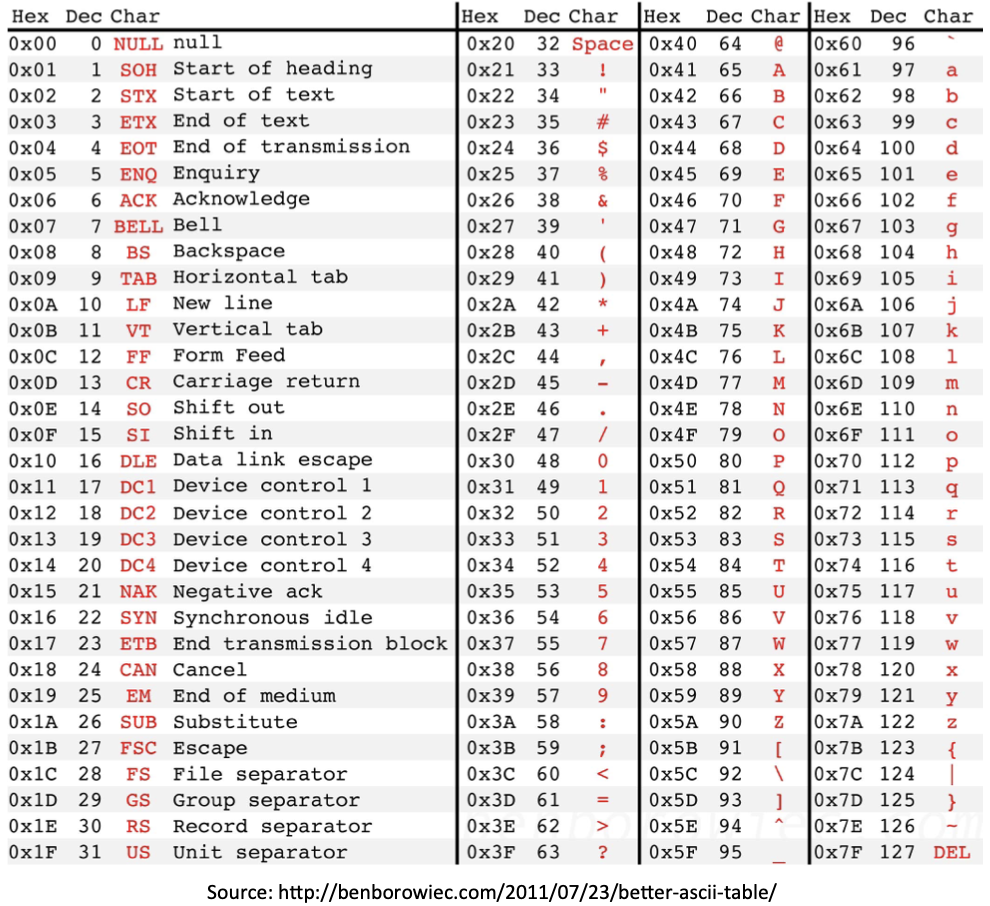
0x1F는 16진법으로는 0001 1111, 아스키 코드로는 1F입니다. 만약 0x1F 값을 파일로 저장할 때, 이 데이터는 두 가지 방법으로 표기될 수 있습니다.
1) native hex : 0001 1111
2) "text" : 아스키코드의 문자 그대로 1F

1-4 Breaking the Vigenère cipher

Vigenère cipher는 key의 알파벳 순서에 맞게 plaintext를 지정된 양만큼 이동해여 암호화를 했습니다. 만약 Vigenère cipher를 코드로 짜야 한다면, 자연스럽게 알파벳 문자를 byte 단위의 ASCII 코드로 변경하여 문제를 해결해야할 것입니다.

| 방법

• 원하는 plaintext와 Key는 ASCII 코드로 표현한다.
• ASCII 코드를 16진법으로 변한다.
• 같은 자리에 있는 비트(bit)끼리 XOR연산을 진행한다.
• 진행한 결과값을 다시 ASCII 코드로 변환하여 암호화를 마무리 한다.

plaintext = "Hello!"를 key = 'A1 2F'로 암호화하는 과정은 아래와 같습니다.

• plaintext = (ASCII) 48 65 6C 6C 6F 21
• key = A1 2F
• cipher text =
  48 65 6C 6C 6F 21
  A1 2F A1 2F A1 2F
  ⇒ XOR ⇒ E9 4A CD 43 CE 0E

| 공격

1. key의 길이 : 암호화 된 문자마다의 빈도수는 다르겠지만, 어떤 특정 간격에서 문자의 빈도수 분포가 실제 영문자의 분포와 비슷하게 나타납니다. 이 지점을 key의 길이로 설정하면 됩니다.
2. key의 각 byte 결정 : key의 길이 (t+n)번 모인 글자는 똑같은 문자로 암호화가 되었으므로, 모든 가능한 byte value B를 통해 이 문자들을 복호화합니다. 이 암호화된 문자들을 stream이라고 합니다.

• Attack time
  • key의 길이: $1 \sim L$
  • key의 길이를 결정하는데 걸리는 시간: $256L$
  • key의 모든 byte를 결정하는데 걸리는 시간 (복호화 완료하는 시간): $256^2L$
  • (brute-force search로 key를 찾는데 걸리는 시간: $256^L$)
  • attack은 암호문의 길이가 길수록 잘 됩니다. 평문이 길어지면 글자 빈도수가 실제 영문자에 나오는 글자 빈도수와 비슷해지기 때문입니다.

1-5 Principles of modern cryptography

고전적인 암호학은 예술로 평가되었습니다. 유물로 나온 암벽화의 그림을 문자로 복호화하는 고고학자들을 상상해보면, 원리가 정해졌다기 보다는 예술이라는 것이 조금 더 설득력있긴 한 것같습니다..
70-80년대에 들어서야 암호학은 과학적 학문으로 발전하기 시작헸습니다. 현대 암호학의 핵심 원리는 다음과 같습니다.
1. Formal definitions, 정의
security에 대한 정의와 수학적인 모델입니다.정의는 효율과 동시에 체계들을 비교하고 의미있는 평가를 가능하게 합니다.

2. Assumptions, 가정
암호학은 측정 가능한 가정을 한 뒤, 이 가정의 무결성을 검증하는 방식으로 암호 알고리즘의 안전성을 체크합니다.

3. Proofs of security, 안전성 입증
악의적인 공격자가 체계를 break하려 할 때 proofs는 중요한 역할을 합니다.

여전히 핵심 정의에 한계가 있다면, 가정을 예증할 방법이 또 다시 필요하다는 것입니다. 가정을 위한 증명의 증명이 필요하기 때문에 완전한 안전성에 도달하기엔 현실적으로는 한계가 존재합니다.

2-1 Perfect secrecy, part 1

어떤 암호 알고리즘이 완전한 안전성을 가지기 위해서는 공격 모델을 극복해야 합니다. 암호 공격이란 공격자가 특정 plaintext를 복구하는 것을 말합니다. 암호 공격 모델은 파워 순서대로 아래와 같습니다.

Ciphertext-only attack
: 1개 혹은 여러개의 암호문만을 가지고 attack 하는 것

• Known-plaintext attack
  - 알려진 평문을 가지고 attack 하는 것
  - attacker가 직접 평문을 선택하여 cipher text를 알 순 없지만, 도청 혹은 그 외의 방식으로 주어진 평문에 대해 cipher text를 알아내, 이를 통해 attack 하는 것
• Chosen-plaintext attack
  - attacker가 직접 평문을 선택해 cipher text를 알아낼 수 있고, 이를 바탕으로 attack 하는 것
  - (ex. hash)
• Chosen-ciphertext attack
  - attacker는 자신이 attack 하고 싶은 plaintext-ciphertext 쌍을 제외한 모든 평문과 암호문에 대해서, 어떤 평문이 어떤 암호문이 되는지 알아낼 수 있고, 반대로 어떤 암호문이 어떤 평문이 되는지 알아낼 수 있어, 이를 바탕으로 attack 하는 것
  - 즉, attacker는 오직 자신이 attack 하려하는 text만을 제외한 모든 text에 대한 암복화 정보를 알고 있는 상태
  - (가정으로만 존재하고 real-world에선 불가능한 모델)
  

위 4가지 모델은 아래로 갈수록 attack의 능력이 더 커진다고 볼 수 있습니다. 가장 마지막에 있는 CCAttack을 막아낼 수 있다면 완벽히 secure한 모델이라고 볼 수 있습니다.

즉 암호 공격을 극복하기 위한 goal은 암호 공격에도 평문을 알아챌 수 없게끔 만드는 것입니다.

Secure encryption

• attacker가 key를 알지 못하는 것 (secure 하지 않음)
• attacker가 cipher text를 통해 plain text를 알아내지 못하는 것 (만약, plain text 전부를 알아내진 못해도 평문의 90%를 cipher text로 알아낼 수 있다면, 이는 secure 하지 않음)
• attacker가 cipher text를 통해 plain text의 어느 한 글자도 알아내지 못하는 것 (만약, plain text는 못알아 내지만, 그 cipher text로 평문과 관련된 또 다른 정보를 알아낼 수 있다면, 이는 secure 하지 않음)
• attacker가 cipher text를 통해 plain text에 대한 어떠한 정보도 알아내지 못하는 것 (secure 함)
  
  

2-2 Perfect secrecy, part 2

완전한 안전성을 달성할 때 계산가능한 범위에서 안전하다고 표현한다고 하였습니다. 이 안전성을 판단하는 척도는 '확률'입니다. 2-2에서는 확률분포의 개념과 이로 판단했을 때의 안전성 여부를 보여주고 있습니다.

| 개념

• Probability

  • Random variable: 특정 확률이 발생할 이산적인 값
  • Event (사건): 특정 상황에 특정 일이 발생하는 것
    ⇒ $Pr[E]$
  • Conditional probability (조건부 확률): 특정 사건 B가 일어난 상황에서, 또 다른 사건 A가 일어날 확률
    ⇒ $Pr[A|B] = Pr[A \; and \; B] \; / \; Pr[B]$
  • Independent (독립): 두 사건 X와 Y가 독립이라면
    ⇒ $Pr[X=x \; | \; Y=y] = Pr[X=x]$
  • Law of total probability (총 확률 법칙): 사건 E1, E2, … , En이 partition일 때, 어떤 사건 A에 대해
    ⇒ $Pr[A] = \sum_{i} Pr[A \; and \; E_{i}] = \sum_{i} Pr[A | E_{i}] \cdot Pr[E_{i}]$

• Private-key encryption scheme

  • $Gen$
  • $c \leftarrow Enc_{k}(m)$
  • $m := Dec_{k}(c)$

• Notation

  • $K$ (key space): 모든 가능한 key의 집합
  • $M$ (plaintext space): 모든 가능한 평문의 집합
  • $C$ (ciphertext space): 모든 가능한 암호문의 집합
  • 위 3가지 집합은 랜덤변수로 나타난다
  • 랜덤변수 $K$와 $M$은 서로 독립이다 (즉, plaintext와 key는 서로 영향을 주지 않는다)

| 예시

shift cipher

• $k \in \{0, ..., 25\} \rightarrow Pr[K=k] = 1/26$
• $Pr[M = \;'a\,'] = 0.7, \; Pr[M = \;'z\,'] = 0.3$
• $Pr[C = \;'b\,'] = \; ?$

평문 M은 ‘a’ 또는 ‘z’일 수 밖에 없다. 그 이유는 2번째 조건에서 M이 ‘a’일 확률과 M이 ‘z’일 확률을 더했을 때 0.7 + 0.3 = 1이 나오기 때문이다. 따라서 암호문 C가 ‘b’가 될 확률은, 평문 M이 ‘a’일 때 k가 1일 확률과, 평문 M이 ‘z’일 때 k가 2일 확률을 더한 것이다.

shift cipher

• $Pr[M = \;'one\,'] = 1/2, \; Pr[M = \;'ten\,'] = 1/2$
• $Pr[C = \;'rqh\,'] = \; ?$

평문 ‘one’에선 k가 3이면 ‘rqh’를 만들 수 있지만, ‘ten’에선 shift cipher 이므로 어떤 k가 들어가도 ‘rqh’를 만들 수 없다.

Perfect Secrecy란?

Perfect Secrecy란 공격자가 cipher text를 통해 plain text에 대한 어떠한 정보도 알아내지 못하는 것을 말합니다. 공격자가 cipher text를 보고나더라도, plain text에 대한 그 어떤 정보도 알아낼 수 없어야 완전히 안전하다고 볼 수 있습니다.

| 예시

shift cipher

• $Pr[M = \;'one\,'] = 1/2, \; Pr[M = \;'ten\,'] = 1/2$
• $Pr[M = \;'ten\,' \; | \; C = \;'rqh\,'] = \; ?$

shift cipher일 때, 암호문 ‘rqh’가 주어지면 평문 ’ten’은 절대 만들 수 없으므로 확률이 0이 된다. 이는 그냥 평문이 ‘ten’일 확률과 다르므로 이 암호체계는 perfect secrecy를 만족하지 않는다.

Bayes’s theorem

베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리입니다. 수식으로 표현하면 다음과 같습니다.

| 예시

shift cipher

• $Pr[M = \;'hi\,'] = 0.3$
• $Pr[M = \;'no\,'] = 0.2$
• $Pr[M = \;'in\,'] = 0.5$
• $Pr[M = \;'hi\,' \; | \; C = \;'xy\,'] = \; ?$
  $Pr[M = \;'hi\,' \; | \; C = \;'xy\,'] = \; ? \\ = Pr[C = \;'xy\,' \; | \; M = \;'hi\,'] \cdot Pr[M = \;'hi\,'] \; / \; Pr[C = \;'xy\,']$

베이즈 정리 이용

평문 ‘hi’를 암호화 했을 때 ‘xy’가 나올 확률은 key의 개수 확률과 같음 (1/26)

암호문 ‘xy’를 만들 확률은 모든 평문에 대해 계산하여 구함

위에서 나온 결과를 대입하여 계산하면, 이 암호체계는 perfect secrecy를 만족하지 않는다는 것을 알 수 있다.

3-1 The one-time pad

Perfect secrecy를 만족하는 암호 스킴이 있을까요? 지금 소개하는 One-Time pad(OTP)가 이애 해당합니다. OTP는 plaintext의 길이와 동일한 space의 key를 가지는 암호화 알고리즘입니다.

| 특징

• $M = \{0, 1\}^n$ (0과 1로 이루어진 길이가 n인 문자열)
• $Gen$: 0과 1로 이루어진 길이가 n인 key
• $Enc {_k}(m) = k \oplus m$
• $Dec {_k}(c) = k \oplus c$
  

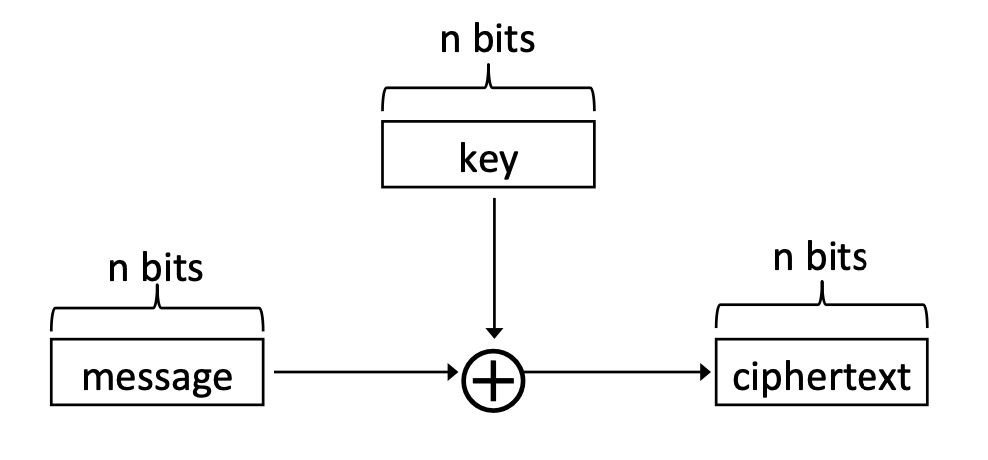
위 그림처럼 OTP는 plaintext, key, ciphertext의 길이가 모두 동일합니다.