[Cryptography(암호학)] 2주차-Computational Secrecy and Principles of Modern Cryptography

본 포스팅은 Coursera | Cryptography - Jonathan Katz 강의를 수강하며 정리했습니다.

1-1 Limitations of the One-Time Pad

Cryptography 2주차 강의정리를 시작하겠습니다. 지난 시간에 One-time pad가 perfect secrecy를 만족한다고 배웠습니다. One-time pad는 현실에서도 사용이 되는 sheme입니다. 1980년대 워싱턴 DC와 모스크바를 연결하던 'red phone'의 key는 trusted couriers이 두 당사자에게 공유키에 사용되는 비트들을 프린트한 서류가방을 서로 공유하여, 실제로 one-time pad를 사용한 바 있습니다. 하지만 지금은 이러한 암호화 방식이 자주 사용되지는 않죠. 그 이유는 one-time pad에는 결함이 존재하기 때문입니다.

1. About one-time pad

One-time pad의 전제 조건은 다음과 같습니다.

1. one-time pad의 key의 길이는 message의 길이보다 크거나 같아야 한다.
2. 하나의 key는 단 하나의 messag만 암호화를 해야 한다.
   (key는 한 번만 사용되어야 한다.)

먼저 첫 번째 조건을 만족시키기 위해서는 암호화를 진행하고자 하는 두 대상자 Alice와 Bob이 매번 메시지만큼 긴 공유키를 메시지가 바뀔 때마다 공유해야 합니다. 간단한 메시지는 몰라도, 책 한 권 분량을 암호화한다고 할 때 정말 긴 key를 공유해야 한다면 매우 비효율적이겠죠.

그럼 두 번째 조건을 살펴봅시다. 하나의 key를 두 번 이상 사용하면 안 될까요? 예시를 들어보겠습니다.

위 예시에서 $m_1$과 $m_2$는 같은 key $k$로 암호화되었습니다. 위처럼 동일한 key로 암호화를 진행할 경우 공격자는 이를 간단하게 뚫을 수 있습니다.

공격자가 두 개의 메시지만 암호화를 요청하더라도 $m_1 \oplus m_2$이라는 메시지에 대한 정보가 바로 유출됩니다. 이는 ASCII 코드로 $m_1$과 $m_2$의 각 자리수의 같고 다름에 대한 정보가 유출되는 것이므로, frequency analysis로 메시지의 정보를 알아낼 수 있습니다. 공격에 취약하다는 것은 더이상 perfact secrecy를 만족시키지 않게 되는 것입니다. One-time pad의 두 전제 조건은 어떻게 보면 암호화를 실제로 구현하기에는 결함이 됩니다.

2. Optimality of the one-time pad

One-time pad의 두 번째 전제 조건이 위배되었을 때 plaintext의 정보가 유출된다는 사실을 위에서 확인했습니다. 조금이라도 one-time pad를 효율적으로 사용할 방법은 없을까요? 그 전에 첫 번째 전제조건에서 $|K| \ge |M|$가 과연 최적의 조건인지에 대해 알아보려고 합니다. One-time pad의 첫 번째 전제조건을 통해 perfect-secrecy를 만족하는 scheme을 정의하면 아래와 같습니다.

| Theorem

만약 message space가 $M$인 ( $Gen$, $Enc$, $Dec$ ) sheme이 perfectly secret 하다면, $|K| \ge |M|$를 만족한다.

| Intuition & Proof

어떤 ciphertext에 대해 $K$ 집합에 있는 모든 원소 $k$로 복호화를 시도한다고 합시다. 만약 $|K| < |M|$라면, 복호화 된 결과값인 $m$의 집합에 없는 메시지가 존재할 수 있습니다. 즉, 모든 $M$의 원소 $m$을 암호화하지 못한다는 이야기입니다.

이는 이론의 대우로 증명할 수 있습니다.

여기서 $M(c)$ 암호문 c를 복호화 했을때 만들어지는 message 들의 집합으로 정의하겠습니다.

그러면 이렇게 만들어진 $M(c)$의 원소 개수는 전체 메시지 집합인 $M$의 원소 개수보다 적을 것입니다. 따라서 어떤 cipher text c는 복호화할 때 $M(c)$에는 속하지 않으면서 전체 메시지 집합인 $M$에만 속하는 특정 message로는 만들어지지 않을 것입니다. 그 확률은 0이 되므로 위 증명을 보일 수 있습니다.

2-1,2 Computational secrecy

One-time pad는 perfect secrecy를 만족하는 scheme입니다. 하지만 두 최적 조건을 만족하기 위해서는 현실적인 결함이 존재했습니다. 즉, 현실적으로 perfect secrecy를 구현하기에는 어려움이 있습니다. 그래서 지금부터 secrecy의 조건을 조금 낮춰 현실적인 perfect secrecy를 달성하는 방법을 알아볼 것입니다.

1. Perfect secrecy

이론 상 perfect secrecy는 "무한한 컴퓨팅 능력을 가진 도청 공격자가 plaintext에 대해 그 어떤 정보도 유추할 수 없는 것"을 말합니다. 하지만 현실적인 sheme은 이를 도달하기도 어려울 뿐더러, 안전성을 불필요할 정도로 강조했습니다. (① 전 무한한 컴퓨팅 능력을 가진 도청 공격자가 존재한다는 가정부터 불필요해 보이고, ② 그 어떤 정보도 유추할 수 없는 것도 과한 것 같습니다..)

2. Computational secrecy

그래서 현실적인 암호학의 secrecy인 computational secrecy를 정의하고자 합니다.

① 무한한 컴퓨팅 능력이 아닌, 일정 수준의 컴퓨팅 능력을 가진 'efficient'한 도청자가 존재한다.
② 아주 작은 확률로 plaintext에 대한 정보를 유추하는 것까지는 허용한다.

②에서 말하는 아주 작은 확률은 $2^{-60}$ 보다 더 작은 확률을 말합니다. $2^{-60}$이 얼마나 작냐면... Alice와 Bob이 동시에 벼락을 맞을 정도의 확률보다 작고, 1,000억 년에 한 번 일어날까 말까 할 정도의 확률이라고 하네요 ^^ (그런데 지금은 $2^{-80}$ 정도의 확률 정도는 되어야하는 것으로 알고 있습니다.) 만약 'efficient'한 공격자가 그 이상으로 공격할 수 있다면, 이 sheme은 computational secrecy를 만족하지 않는 것입니다.

'efficient'한 공격자는 현실 세계에서 '컴퓨터로 공격하는 도청자'라고 생각하면 편합니다. 일반적인 데스크탑 컴퓨터에서 공격을 실행하는 공격자는 무차별 공격으로 매년 약 $2^{57}$ 만큼의 키를 테스트 해볼 수 있습니다. (데스크탑 컴퓨터가 1년 동안 쉬지않고 실행될 때의 평균 클럭 주기입니다.) 슈퍼 컴퓨터를 사용하는 공격자는 1년에 약 $2^{80}$ 만큼의 키를 테스트할 수 있는 능력을 가집니다. 슈퍼 컴퓨터를 빅뱅이 일어난 시기부터 공격을 진행했다면 $2^{112}$ 개의 키를 테스트할 능력을 가지는 것입니다. 따라서 현재는 key space를 $2^{128}$ 혹은 그 이상으로 설정합니다.

3. Perfect indistinguishability

이제 암호학에서의 secrecy가 조금 현실적인 모습을 보이는 것같나요? 하지만 아직 끝나지 않았습니다 ... 위의 computational secrecy에서 우리가 본 'efficient'한 공격자는 무차별 공격을 수행해서 실제 plaintext를 찾아내는 것을 목표로 합니다. 하지만 이런 공격이 실제로 가능하려면, 1 bit의 key부터 시작해 맞는 key를 발견할 때까지 무차별 공격만 주구장창 해야만 합니다. 암호화 scheme을 깨는 일을 제외하곤 그 어떤 테스크도 처리하지 않은 채로요. 현실적으로 이런 공격을 만들기는 여전히 어렵습니다. 이런 개념에서 볼 때, 현실성을 더하고자 조금 더 secrecy의 정도를 낮춰도 괜찮아보이지 않나요?

그 정도를 완화하고자 등장한 개념이 perfect indistinguishability입니다. 말 그대로 실제ciphertext와 random message를 구분할 수 없다면(indistinguishable) 안전하다고 판단하는 것입니다. 판별 과정은 아래와 같습니다.

1. Attacker $A$가 message space $M$에서 $m_0$와 $m_1$을 뽑아 Challenger에게 건낸다.
2. Challenger의 암호화 sheme은 $m_0$와 $m_1$ 중 하나를 랜덤하게 선택하여 암호화하여 출력한다.
3. Attacker는 ciphertext $c$가 $m_0$와 $m_1$ 중 어떤 message를 암호화 했는지 맞춘다.
4. 이때 plaintext를 맞출 확률이 $1/2$라면, 이 암호화 scheme은 perfect indistinguishability를 만족한다.

이 과정을 formal하게 정리해 봅시다.

암호화 sheme $\mathrm{\Pi}$와 공격자 $Adversary$를 위처럼 정의했을 때, 확률 $PrivK_{A,\mathrm{\Pi}}$는 아래 그림과 수식처럼 표현 가능합니다.

$1.\;\;A \;\; outputs \;\; m_0, m_1 \in M \\$
$2.\;\;k \leftarrow Gen, \;\; b \leftarrow {0, 1}, \;\; c \leftarrow Enc_k(m_b) \\$
$3.\;\;b' \leftarrow A(c); \;\; A \; succeeds \; if \; b = b', \; and \; experiment \; evaluates \; to \; 1 \; in \; this \; case\\$

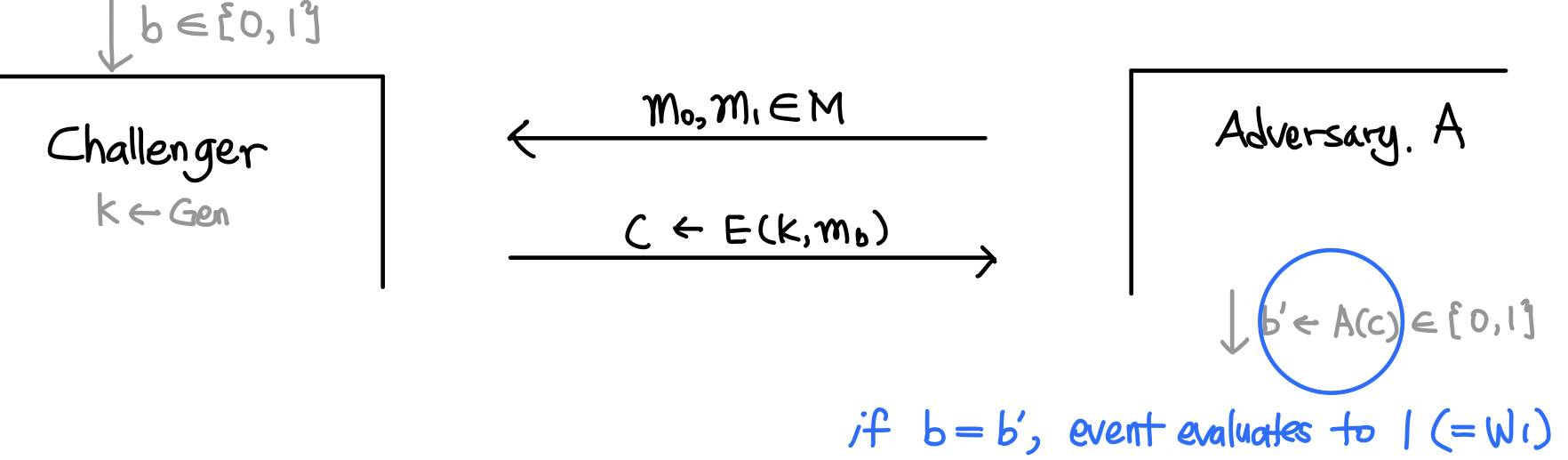
Event가 1(공격자가 성공하는 사건)일 때의 확률이 $1/2$ 라면, perfect indistinguishability을 만족합니다.

암호화 sheme $\mathrm{\Pi}$가 perfect indistinguishability를 만족한다면, 필요충분조건으로 $\mathrm{\Pi}$는 perfect secrecy 또한 만족합니다. 완화된 개념이라고는 하지만, indistinguishability 또한 매우 충족하기 어려운 개념이라는 점에서 암호학에서는 perfect secrecy를 perfect indistinguishability로 대체합니다.

4. Computational indistinguishability

이번엔 perfect indistinguishability의 개념의 정도를 조금 더 완화해서 생각해 봅시다. Perfect indistinguishability에서는 암호화 scheme이 암호화 한 plaintext를 맞출 확률이 $1/2$이어야 합니다. 암호화 sheme $\mathrm{\Pi}$에 대해 공격자가 성공할 확률이 정확히 $1/2$가 되려면 Computational indistinguishability의 개념에서는 공격자가 최대 $t$ 번의 공격을 실행할 때의 확률을 $1/2 + \epsilon$으로 둡니다. $t$와 $\epsilon$은 현실에서의 오차범위를 고려하기 위한 파라미터입니다. 무한대의 공격을 할 수 없다는 점에서 공격자 $A$의 공격 횟수를 $t$로 제한하고, $\epsilon$의 매우 작은 오차범위를 두었습니다. Computational indistinguishability는 두 가지 방식으로 정의할 수 있습니다.

• Concrete security

Concrete security는 보안에 대한 수치적/실천적 접근법입니다. 다항 시간 내에 허용되는 범위에서 성공할 확률을 구합니다.

정해진 시간 $t$ 동안 모든 공격자 $A$가 암호화 scheme을 맞출 확률이 $1/2 + \epsilon$ 보다 작다면 computational indistinguishability를 만족합니다.

• Asymptotic security
  

Asymptotic security는 concrete security보다는 이론에 가까운 개념입니다. 다항 시간 공격을 지속했을 때 안전하다면, polynomial-time reduction이 가능하다고 보아 security를 정의했습니다. 즉, t번 시간동안 암호화 scheme이 안전할 때, 계속된 PPT(probabilistic polynomial-time) 내에 계산할 수 있는 효율적(efficient)인 알고리즘의 공격에도 안전하다고 보는 것입니다. 다만 안전성의 효율성(security level)을 측정하기 위해 concrete security 정의에서 security parameter $n$의 개념을 추가했습니다. $n$은 negligible function을 정의하기 위해 필요한 파라미터로, negligible 하다면 무시해도 될 정도로 작은 값이라는 것을 나타냅니다.

즉, PPT 공격자 $A$가 맞출 확률이 $1/2 + \epsilon(n)$ 보다 작다면 computational indistinguishability 합니다.

5. Encryption and plaintext length

암호화 scheme을 공격하는 PPT는 주어진 ciphertext를 보고 brute-forces 공격을 통해 무작위로 plaintext를 구하고자 합니다. 하지만 완전히 무차별 공격은 아닙니다. 지금까지 배운 암호화 scheme들은 ciphertext와 plaintext의 길이가 동일했습니다. OTP같은 경우는 key의 길이도 동일했고요! 따라서 공격자는 ciphertext의 길이를 보고 plaintext의 길이를 추측할 수 있기 때문에, ciphertext에서 plaintext에 대한 정보를 완전히 주지 않는 것은 불가능합니다. 앞으로의 암호화 scheme에서는 이러한 문제까지 해결하는 것을 목표로 진행할 것입니다.

3-1 Pseudorandomness

1. Random

Pseudorandom의 개념을 보기 전에, random의 의미를 살펴봅시다.

$0101010101010101 \\ 0010111011100110\\ 0000000000000000\\$

16 bits 짜리 문자열 세 개 입니다. 한 비트 당 0 혹은 1이 발생할 확률이 동등하다고 가정하면 $1/2$이므로, 16 비트 짜리 문자열 하나가 발생할 확률은 동등하게 $2^{-16}$입니다.

앞으로 "random"의 의미는 확률적으로 동등하게 분배된, "uniform"과 같다고 정의하겠습니다. 여기서 중요하게 짚고 넘어가야하는 것은, 문자열 자체의 특징을 random으로 정의하는 게 아니라 문자열 집합에서 문자열이 뽑힐 확률 분포를 random으로 정의하는 것입니다. 쉽게 말하면, 그 어떤 16 비트 문자열도 다른 16 비트 문자열보다 더 랜덤하다고 말할 수 없이 전부 "동등"해야 합니다. 위 예시에서 세 문자열이 뽑힐 확률이 전부 다 같았던 것처럼 말이죠. 그럼 random하다면, 모든 확률의 총합이 1인 uniform distribution에서 n 비트의 문자열이 나올 확률은 전부 동일하게 %2^{-n}% 이어야 합니다. 정의는 아래와 같습니다.

2. Pseudorandom

Pseudorandom은 쉽게 말하면 random이 아니지만 random처럼 보이는 것을 말합니다. 집합에서 나온 문자열이 uniform한지 아닌지 구별하지 못하도록 만들면 됩니다.

| Take 1

확률분포 D에서 x만큼의 샘플을 뽑았다고 가정합시다. 이때 x가 균등분포에서 선택된 표본이라면, 첫 번째 비트가 1이 될 확률은 $1/2$에 가까울 것입니다.

동일한 원리로, 첫 번째 비트 이후 다음 비트들도 각각 1 발생 확률은 $1/2$일 것입니다.

이는 통계적으로 분포 D에서 추출된 x에 대하여 20개 까지의 비트에서 1이 추출될 확률이 실제 random한 전체 분포 U에서의 발생확률과 비슷하다면 D를 pseudorandom하다고 볼 수 있습니다.

| Take 2

다시 암호학에서의 security의 정의에 대해 생각해봅시다. 앞서 우리는 계속된 PPT(probabilistic polynomial-time) 내에 계산할 수 있는 효율적(efficient)인 알고리즘의 공격에도 안전하다면 암호학에서의 security를 보장한다고 배웠습니다. Take 1에서 본 pseudorandom의 정의로는 20 번의 시도에 대해서만 다루고 있지만, 암호학에서의 공격자(adversary)는 PPT로 20 비트가 아닌 다른 테스트를 진행할 수도 있습니다. 그렇다고 pseudorandom은 진짜 random은 아니기 때문에, 확률분포 D가 완전한 random이 아니어야하고, 그 말은 언제나 모든 PPT의 확률 테스트를 통과해야하는 것도 아닙니다.(모든 테스트를 통과하면 완전 random과 같아지게 될테니까요! pseudorandom과 random은 엄연히 다릅니다.) 따라서 확률분포 D가 모든 효율적인(efficient) PPT의 테스트를 통과한다면 pseudorandom으로 간주합니다.

| 정의

Pseudorandom도 concrete / asymptotic 두 가지 방식으로 정의할 수 있습니다. 전자로 정의하면 아래와 같습니다.

공격자 $A$가 완전히 uniform한 분포에서 random으로 value를 선택했을 때 맞출 확률과, preudorandom으로 value를 선택했을 때 맞출 확률의 차이가 무시할 수 있을 정도로 작아야 합니다. 위 식에서 $\epsilon$을 negligible function으로 바꾸어 식을 유도하면, asymptotic 하게 정의도 가능합니다.

3-2 Pseudorandom generators

1. Pseudorandom (number) generators (PRGs/PRNGs)

PRG는 의사난수생성기입니다. (한국말은 참 어렵네요..) 단어 하나하나를 뜯어 살펴보면, 짧고 uniform한 시드나 입력을 더 긴 pseudorandom으로 확장해주는 efficient하고 deterministic한 알고리즘을 말합니다.

쉽게 말해, 작은 시드를 넣으면 시드보다 길이가 긴 pseudorandom을 출력하는 확장기라고 보면 됩니다. 그림을 보면 이해가 쉽습니다.

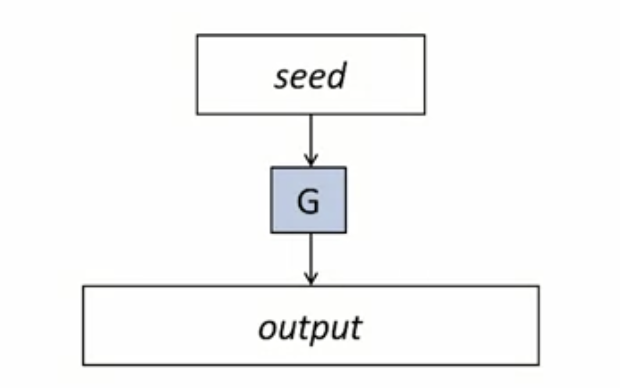
| 등장 배경

Perfect secrecy를 만족하는 OTP(One-Time Pad)의 한계는 key의 길이가 plaintext의 길이와 같아야하는 점이었습니다. 이러한 한계를 극복하고자, key의 길이를 plaintext의 길이보다 작게 만들면서 perfect secrecy를 만족하게 할 순 없을까에 대해 고민했습니다.
Perfect secrecy는 결국 computational indistinguishability를 만족하면 암호학에서 안전하다고 본다고 배웠습니다. 구분이 불가능하다는 것은 완전히 random 분포에서의 추출과 pseudorandom 분포에서의 추출을 서로 구분할 수 없다는 것을 말합니다. 즉, pseudorandom을 만들 수 있다면 암호학에서의 secrecy를 만족할 수 있습니다!

PRG는 많은 점에서 유용합니다. 길이가 작은 plaintext에 대해서는 같은 길이의 key를 만드는 것이 어렵지 않지만, 길이가 매우 큰 10,000 비트 정도의 plaintext에 대해서는 완전히 random하게 비트를 뽑긴 어려울 것입니다. 이때 PRG를 사용하면 아주 작은 시드만으로 긴 길이의 key를 만들어주기 때문에 굉장히 편리합니다.

| 정의

PRG를 정의하겠습니다. PRG는 결정론적이고(determistic) 효율적인(efficient) 알고리즘이라고 앞서 설명했습니다. 결정론적(determistic)이라는 것은 같은 입력을 넣었을 때 언제나 같은 출력이 나오는 것을 말합니다. 효율적(efficient)이라는 것은 다항 시간 내에 풀 수 있음을 말합니다.
이 알고리즘은 pseudorandom을 만들어주는 generator이므로 G라고 정의하겠습니다. Pseudorandom한 key를 출력하는 G의 결과값은 plaintext의 길이보다 크거나 같아야 합니다. (One-time pad의 정의를 생각해보세요.) 그리고 당연히 샘플링한 시드보다 길이가 커야 합니다.
시드를 $x$라고 할 때, generator로 나온 결과값의 길이인 $|G(x)|$는 x의 길이에 대해 poly-time이 걸린다는 점에서 plaintext의 길이인 $p(|x|)$과 같습니다.

p(n) 만큼의 길이를 가진 문자열에 대하여 uniform한 집합 $U_n$의 결과값 $G(x)$의 분포를 D라고 합시다. generator $G$는 ${D_n}$이 pseudorandom한 분포일 때 PRGs를 만족합니다. 공격자 A는 uniform한 문자열 y와 $G(x)$를 구분할 수 없어야 합니다. 전체 확률분포와 D를 비교했을 때 만족해야하는 확률은 다음과 같습니다.

3-3 The Pseudo One-Time Pad

PRG가 등장함으로써 작은 시드를 Generator $G$에 넣어 pseudorandom한 key를 생성할 수 있었습니다. 우리가 지금까지 perfect secrecy부터 PRG를 배웠던 이유는 One-Time Pad때문이었습니다..! key의 길이가 비효율적으로 커야만 했던 OTP의 문제를 PRG가 효율적으로 해결해줄 수 있기 때문입니다. 이를 OTP에 적용하는 방법을 알아봅시다.

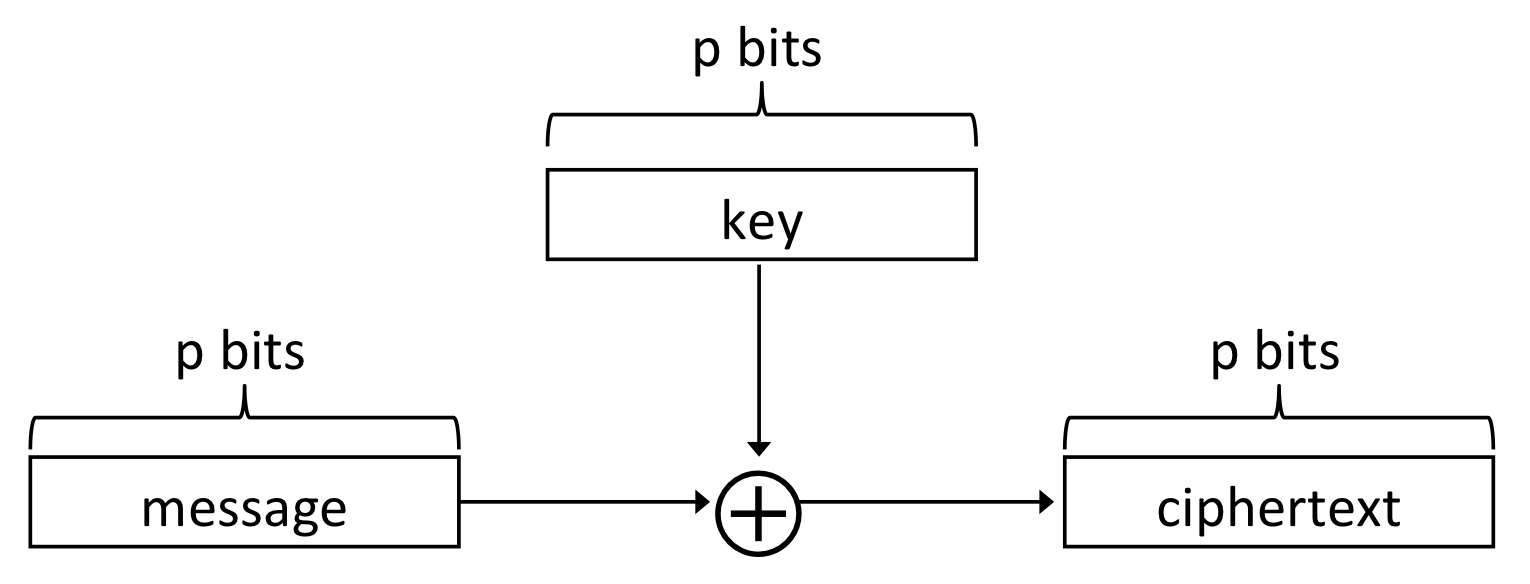
지난 포스팅에서 다룬 OTP의 도식도입니다. 이 도식도에서 key에 해당하는 부분에 PRG를 도입하면 아래와 같습니다.

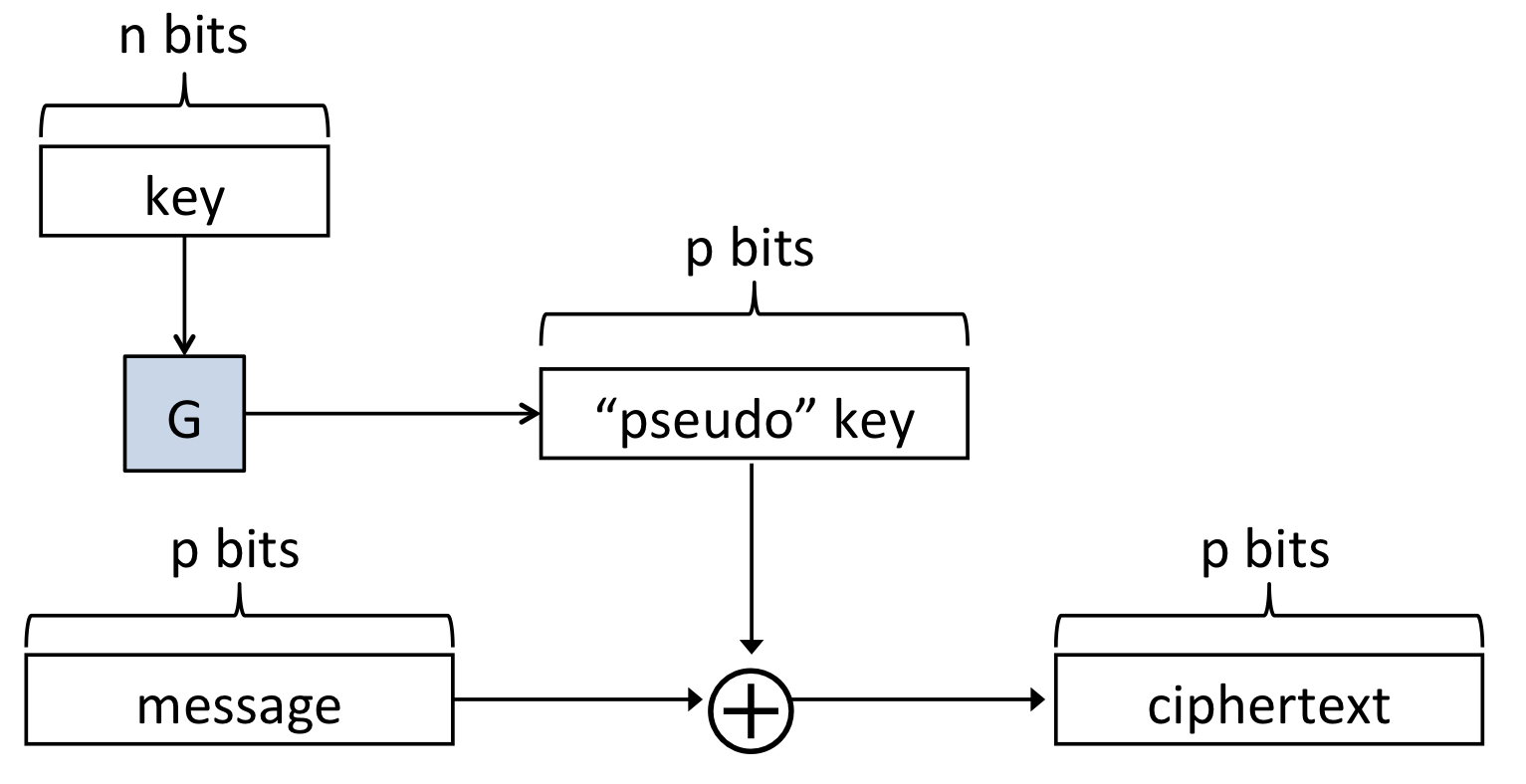
n비트의 작은 랜덤 시드를 Generator $G$의 입력값으로 넣어, plaintext와 같은 비트의 pseudorandom key를 생성하는 원리입니다. 정리하면 아래와 같습니다.

Pseudo-OTP 정의

• $G$: Pseudorandom generator ($|G(k)| = p(|k|)$
• $Gen(1^n)$: 0과 1로 이루어진 n-bit key $k$ 생성
• $M = \{0, 1\}^{p(n)}$ (0과 1로 이루어진 p-bit 문자열)
• $Enc {_k}(m) = G(k) \oplus m$
• $Dec {_k}(c) = G(k) \oplus c$

4-1 Proofs of Security

1. Proof by reduction

지난 포스팅에서 암호학의 세 가지 원칙으로 definitions, assumptions, proofs 이렇게 세 가지를 확인했습니다. pseudo-OTP의 security를 완벽히 증명하는 것은 다소 어렵습니다. Pseudo-OTP의 computational secrecy는 현재로서는 완전히 증명되지 않습니다. 그래서 Secrecy를 증명하기 위해 포함관계를 이용하려고 합니다. Pseudo-OTP의 안전성은 Generator G의 안전성에 있다고 봐도 무방합니다. 따라서
PRG에서 G의 안전성을 증명하고, PRG → Pseudo-OTP임을 증명하면, Pseudo-OTP 또한 안전하다는 것을 알 수 있습니다.
Reduction의 과정 중 모순을 이용한 방법은 다음과 같습니다.

1. $G$를 pseudorandom generator로 가정한다.
2. efficient한 공격자 A가 pseudo-OTP scheme을 깰 수 있다고 가정한다.
3. A를 이용하여 $G$를 깰 수 있는 효율적인 알고리즘 D를 만들 수 있다.
4. Pseudorandom generator $G$를 깨는 D는 존재하지 않는다.
5. 그런 D를 만들도록 돕는 A 또한 존재하지 않는다.

그럼 이번엔 모순을 사용하지 않고, 공격자 A의 공격 성공 확률을 이용한 방법을 보겠습니다.

1. $G$를 pseudorandom generator로 가정한다.
2. efficient한 임의의 알고리즘 A를 수정하여 pseudo-OTP scheme을 공격한다.
3. A를 이용하여 $G$를 깰 수 있는 효율적인 알고리즘 D를 만든다.
4. D가 효율적인 알고리즘이므로, D와 어떤 임의의 알고리즘을 구분힐 확률이 무시할 정도(negligible)여야 한다.
5. 그런 D를 만들도록 돕는 A 또한 무시할 정도(negligible)의 확률을 지녀야 한다.
   
   

2. Security theorem

이제 본격적으로 pseudo-OTP에 대한 증명을 진행하겠습니다. 증명하고자 하는 바는 다음과 같습니다.

$G$가 pseudorandom generator라면, pseudo one-time pad는 computational indistinguishability를 만족한다.

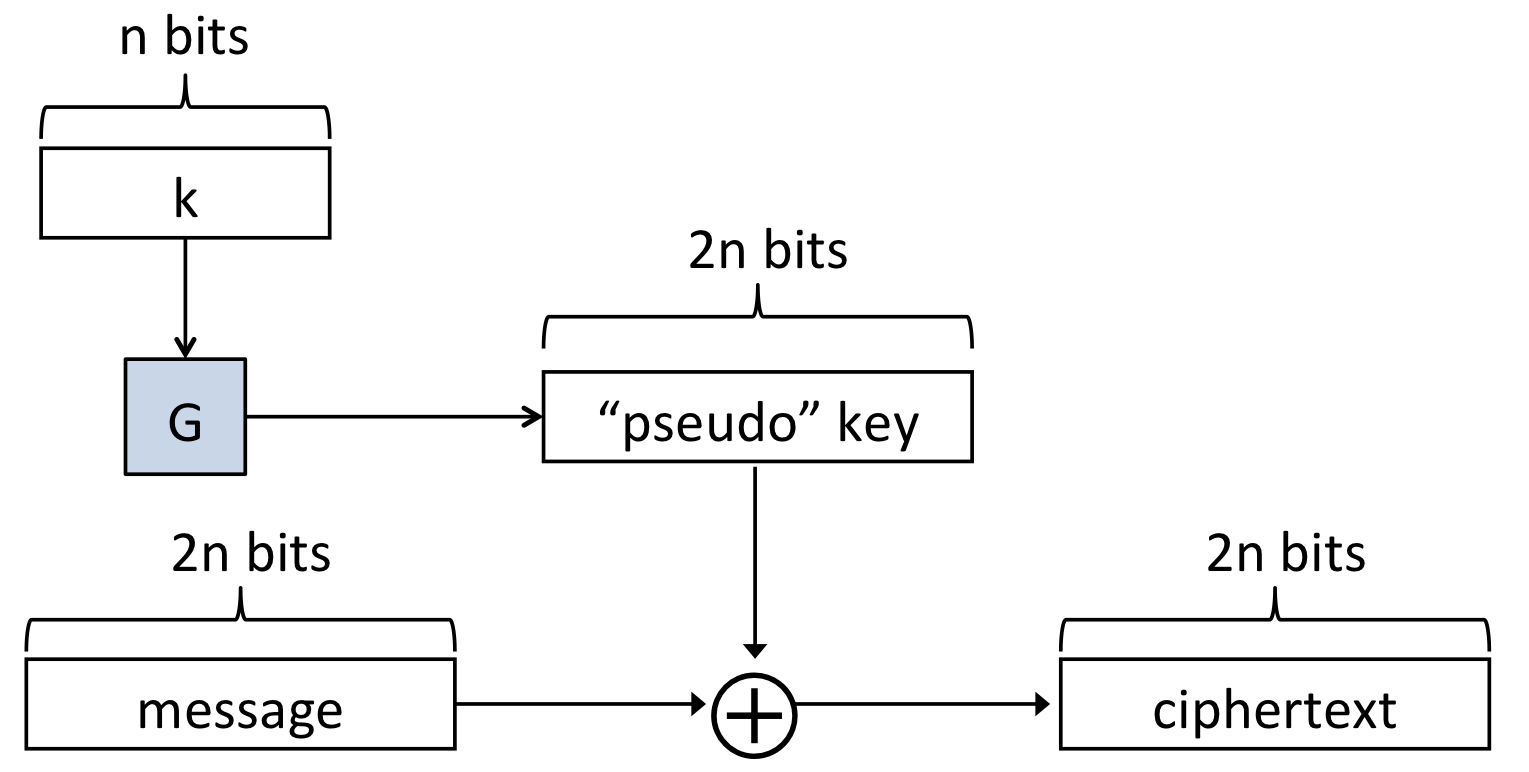
증명을 위해, 위 그림처럼 generator $G$가 시드 길이의 두 배를 출력한다고 가정합시다.

| The reduction

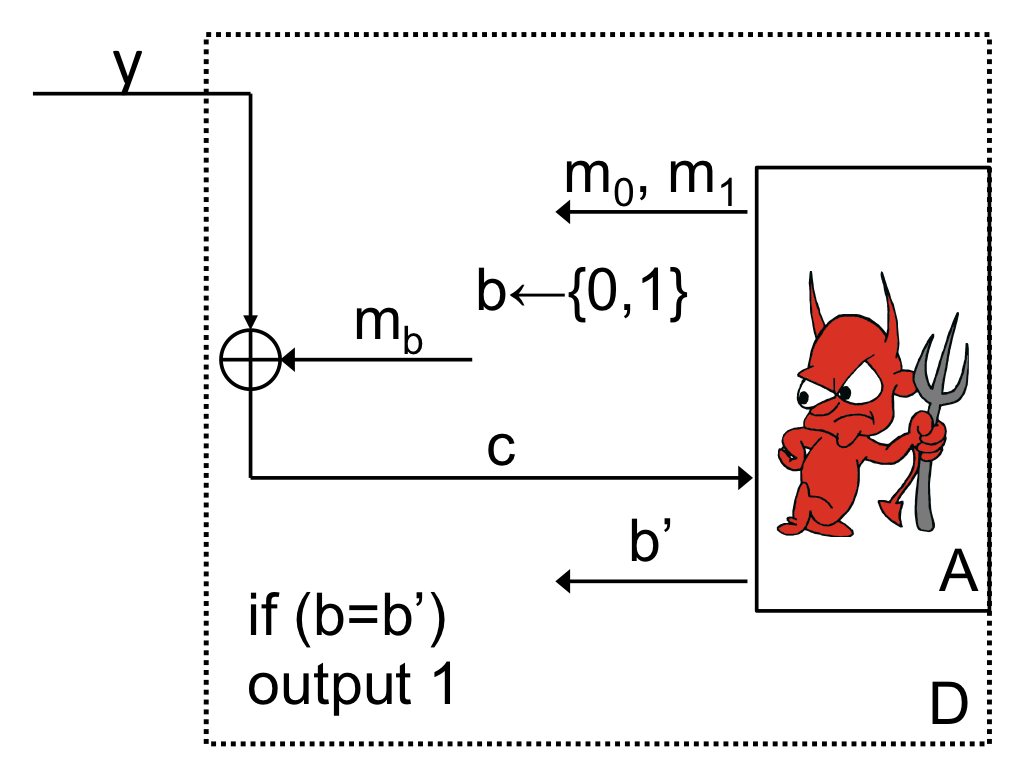
위 그림은 PPT A를 이용한 알고리즘 D의 진행 과정힙니다. 공격자 $A$가 메시지 $m_0$와 $m_1$을 암호화 sheme에게 보내는 것으로 시작합니다. 이 sheme은 두 메시지 중 하나의 메시지를 랜덤으로 선택해 key $y$로 암호화를 진행합니다. 이렇게 생성된 ciphertext $c$를 공격자가 받아, 공격자가 $m_0$와 $m_1$ 중 어떤 메시지를 암호화 했는지 알아 맞추는 과정을 거칩니다. computational secrecy를 보일 때 설명했던 내용과 동일하죠?

이때, input $y$를 이제 pseudorandom으로 바꿔 우리가 증명하고자 하는 과정으로 바꿔봅시다.

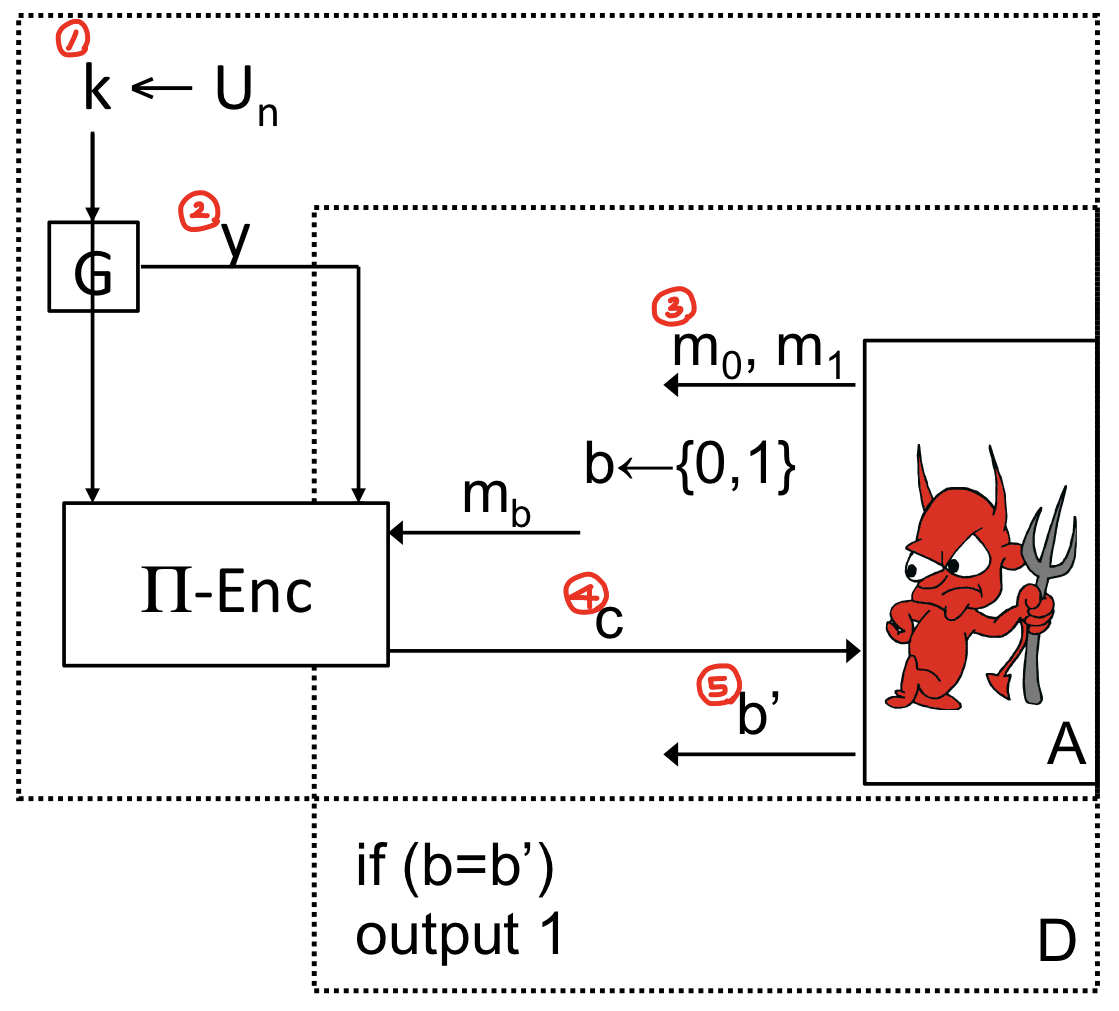
단계별로 하나씩 살펴봅시다. 먼저 generator $G$는 시드가 될 uniform한 key를 뽑아 pseudorandom한 key인 $y$를 출력합니다. 공격자 A는 두 메시지 $m_0$와 $m_1$을 전송하고, 암호화 scheme은 두 메시지 중 하나를 랜덤하게 선택하여 암호화된 ciphertext $c$를 공격자에게 전송합니다. 공격자는 $c$가 어떤 문자를 암호화한 것인지 0 또는 1을 출력합니다. 공격자의 성공확률을 $\mu(n)$로 정의합시다.

이때 y가 uniform하다면, A의 성공확률은 $1/2$에 가까울 것입니다.

그리고 $G$는 pseudorandom을 만족시키는 generator이기 때문에 아래와 같은 식이 성립하고, 이 때문에 pseudo-OTP는 computationally indistinguishable 하다고 볼 수 있습니다.