기본적인 정렬 알고리즘

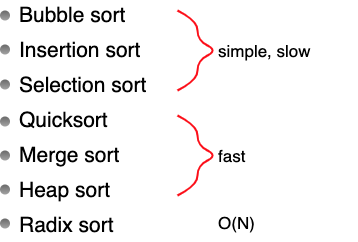
Selection Sort

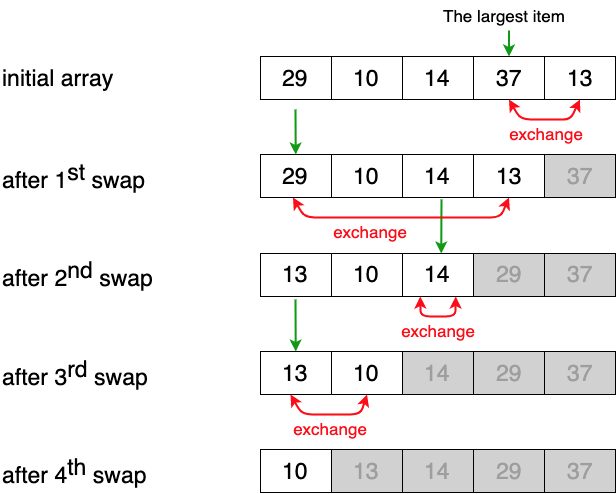
• 각 루프마다
  • 최대 원소를 찾는다
  • 최대 원소와 맨 오른쪽 원소를 교환한다
  • 맨 오른쪽 원소를 제외한다
• 하나의 원소만 남을 때까지 위의 루프를 반복

Pseudo code

SelectionSort(A[], n) // 배열 A[1...n]을 정렬한다.
{
    for last // n downto 2 {            ------------- ①
        A[1...last] 중 가장 큰 수 A[k]를 찾는다; ------------- ②
        A[K] <-> A[last]; // A[K]와 A[last]의 값을 교환  ------ ③
    }
}

실행 시간

1. ①의 for 루프는 n-1번 반복
2. ②에서 가장 큰 수를 찾기 위한 비교횟수: n-1, n-2, ..., 2, 1
3. ③의 교환은 상수 시간 작업

시간 복잡도

• T(n)=(n-1)+(n-2)+...+2+1 = O(n2)
• 평균, 최선, 최악의 경우는 동일하다.

Bubble Sort

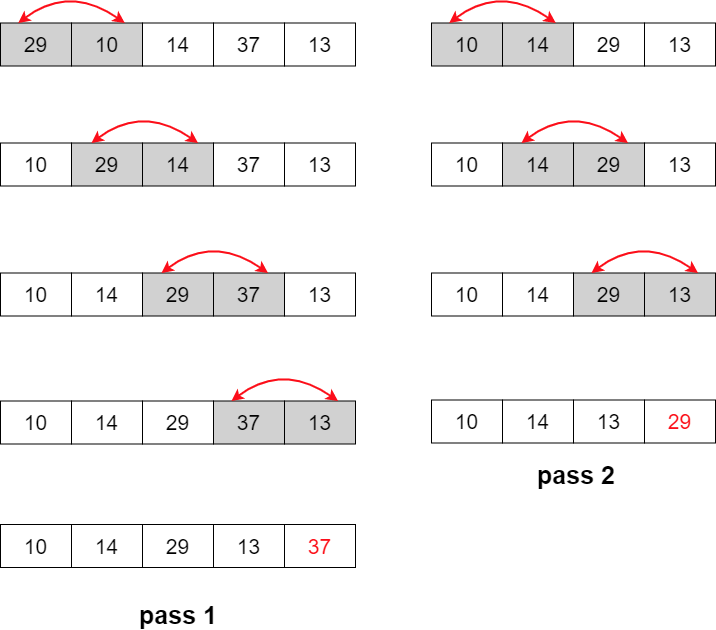
Pseudo code

BubbleSort(A[], n) //배열 A[1...n]을 정렬한다.
{
    for last // ndownto2 {   ------------- ①
        for i -> 1 to last-1    ------------- ②
        if (A[i]>A[i+1]) then A[i] <-> A[i+1]; // 교환 ------- ③
    }
}

수행 시간

1. ①의 for 루프는 n-1번 반복
2. ②의 for 루프는 각각 n-1, n-2, ... ,2 ,1번 반복
3. ③의 교환은 상수 시간 작업

시간 복잡도

• T(n)=(n-1)+(n-2)+...+2+1 = O(n2)
• 평균, 최선, 최악의 경우는 동일하다.

Insertion Sort

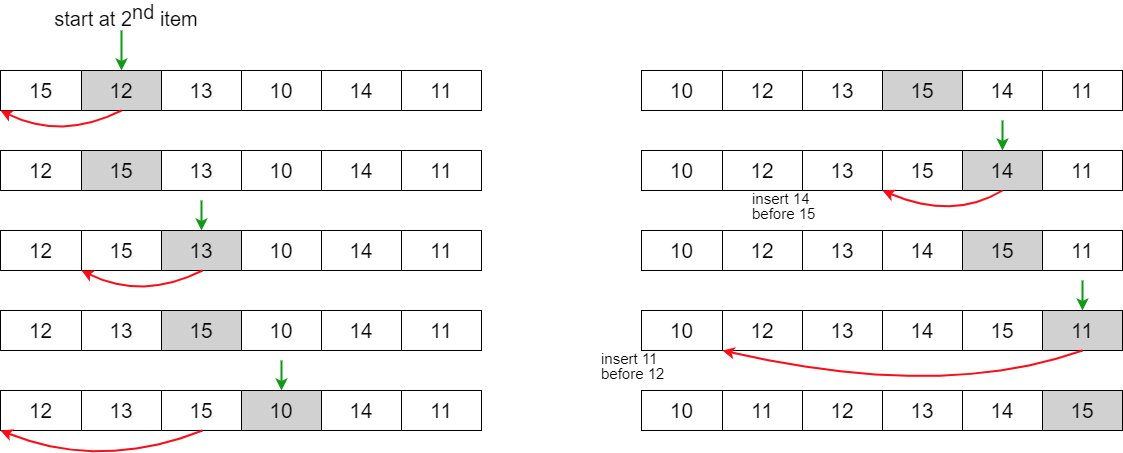
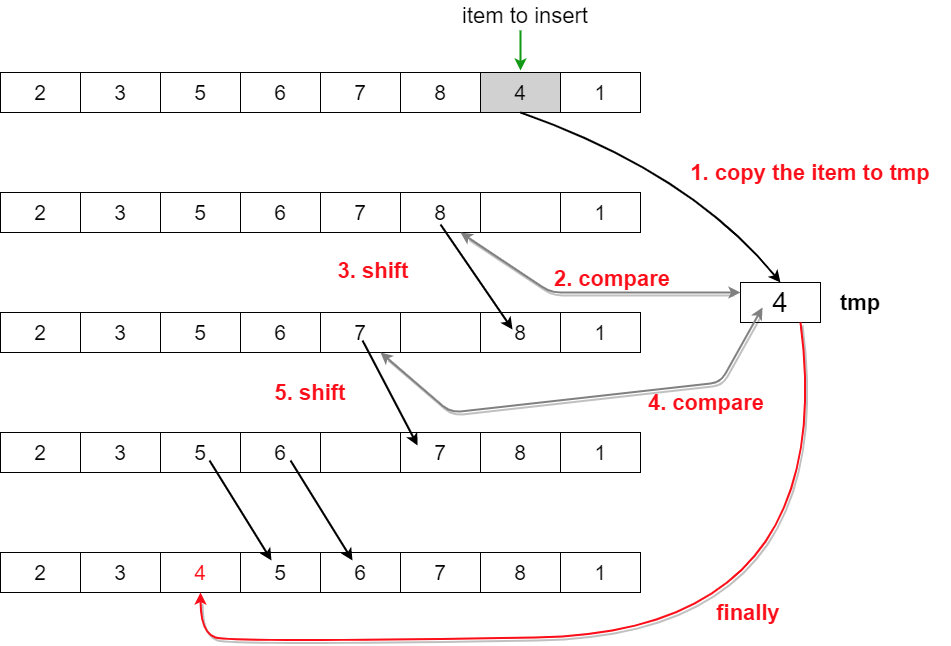
Pseudo code

InsertionSort(A[], n)//배열 A[1...n]을 정렬한다.
{
    for i // 2 to n ------------- ①
      A[1...i]의 적당한 자리에 A[i]를 삽입한다. ------------- ②
}

수행 시간

1. ①의 for루프는 n-1번 반복
2. ②의 삽입은 최악의 경우 i-1번 비교

시간 복잡도

• 최악의 경우: T(n)=(n-1)+(n-2)+...+2+1 = O(n2)

Reference

• 인프런, "영리한 프로그래밍을 위한 알고리즘 강좌, 제3강 기본적인 알고리즘,https://www.inflearn.com/course/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B0%95%EC%A2%8C/dashboard(2020.05.15)