분할 정복
- 분할: 해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할
- 정복: 각각의 작은 문제를 순환적으로 해결
- 합병: 작은 문제의 해를 합하여(merge) 원래 문제에 대한 해를 구함
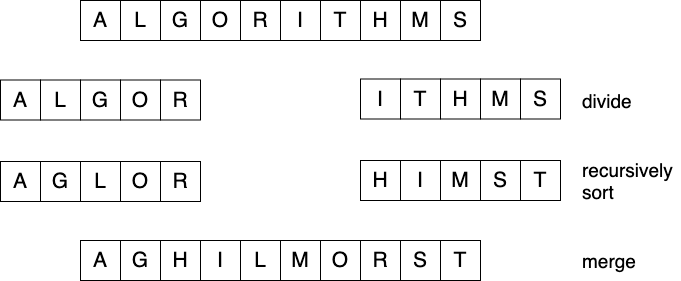
Merge Sort
- 데이터가 저장된 배열을 절반으로 나눔
- 각각을 순환적으로 정렬
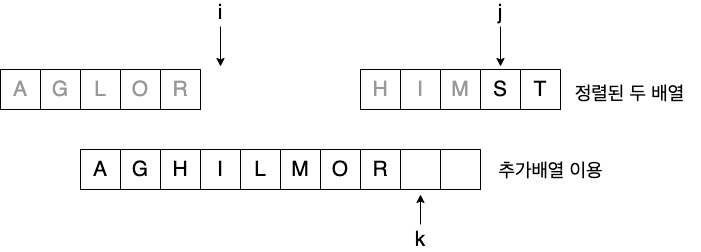
- 정렬된 두 개의 배열을 합쳐 전체를 정렬
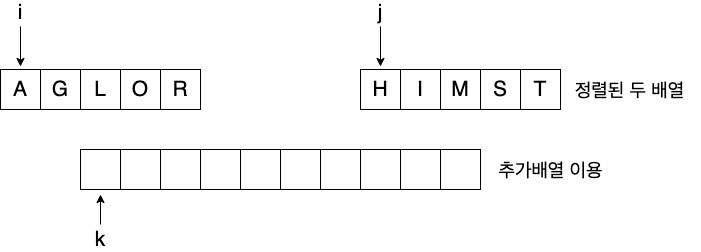
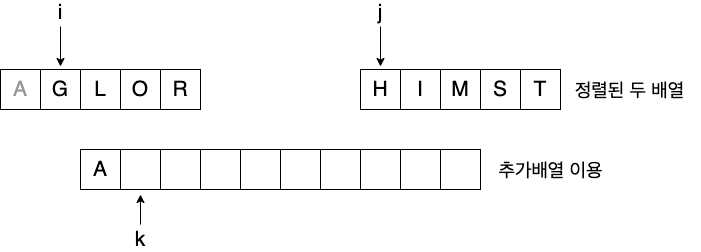
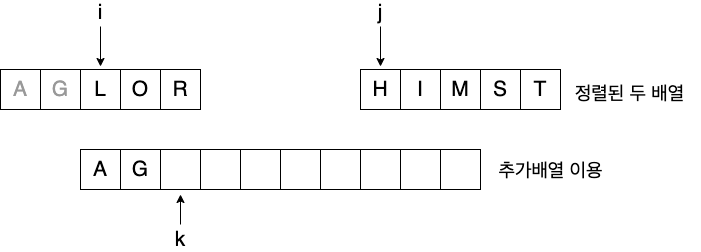
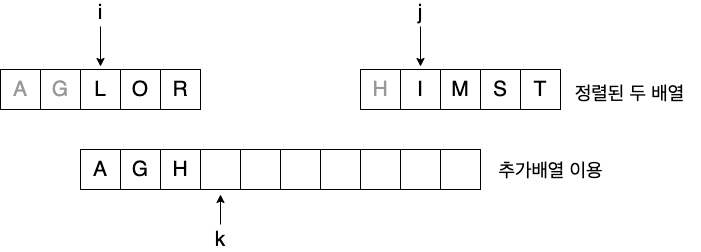

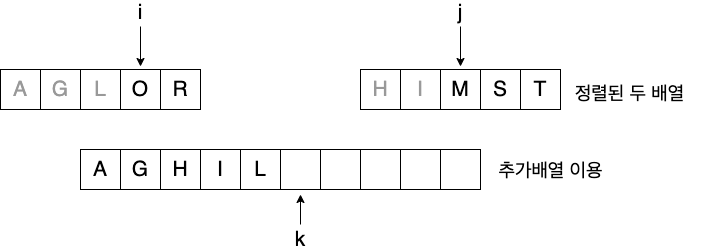
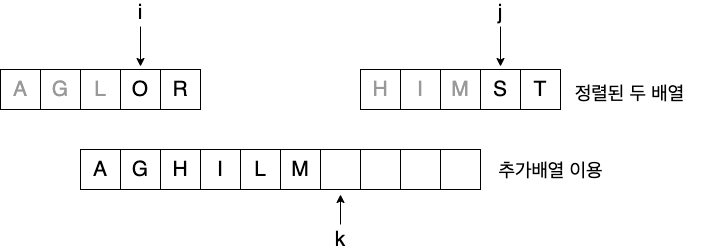
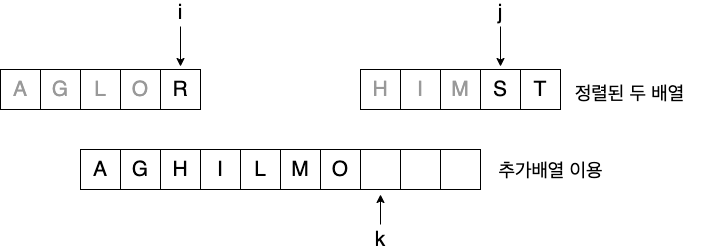

Pseudo code
mergeSort(A[], p, r) ▷ A[p...r]을 정렬한다
{
if (p < r) then {
q ← (p+q)/2; ----------------- ① ▷ p, q의 중간 지점 계산
mergeSort(A, p, q); ---------- ② ▷ 전반부 정렬
mergeSort(A, q+1, r); -------- ③ ▷ 후반부 정렬
merge(A, p, q, r);------------ ④ ▷ 합병
}
}
merge(A[], p, q, r)
{
정렬되어 있는 두 배열 A[p...q]와 A[q+1...r]을 합하여
정렬된 하나의 배열 A[p...r]을 만든다.
}Code
void merge( int data[], int p, int q, int r){
int i = p, j = q+1, k = p;
int tmp[data.length()];
while (i <= q && j <= r) {
if (data[i] <= data[j])
tmp[k++] = data[i++];
else
tmp[k++] = data[j++];
}
while (i <= q)
tmp[k++] = data[i++];
while (j <= r)
tmp[k++] = data[j++];
for (int i = p; i <= r; i++)
data[i] = tmp[i];
}시간 복잡도
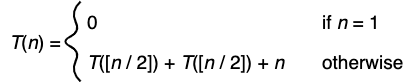
- => O(nlogn)
Reference
- 인프런, "영리한 프로그래밍을 위한 알고리즘 강좌, 제4강 합병 정렬, https://www.inflearn.com/course/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EA%B0%95%EC%A2%8C/dashboard(2020.05.19)
