문제
BOJ 12865 : 평범한 배낭 - https://www.acmicpc.net/problem/12865
풀이
DP문제로 유명한 배낭 알고리즘(Knapsack algorithm)으로 풀이하는 문제이다.
무게가 0일때, 1일때, 2일때, ... k일때까지
1번 item만 넣었을 경우, 2번 item까지 넣었을 경우, ..., n번 item까지 넣었을 경우 와 같은 순서로 dp 테이블을 작성하면 된다.
핵심은 이거다.
무게 w에서 넣을 수 있는 item(물건)의 최대 가치를 저장한다!-
우선 무게 w에서 이전 물건(
i-1번 item)을 넣었을 때의 최대 가치 값을 그대로 가져온다. (dp[i - 1][k]) -
그리고 무게 w에서 지금 물건(
i번째 item)을 넣을 수 있다면,i번째 item의 무게가 w보다 작거나 같을 경우, 짐을 더 넣을 수 있는지를 확인해서 합한 값이 더 가치가 크다면 갱신해준다.
예제의 최종 dp 테이블 값은 아래와 같다.
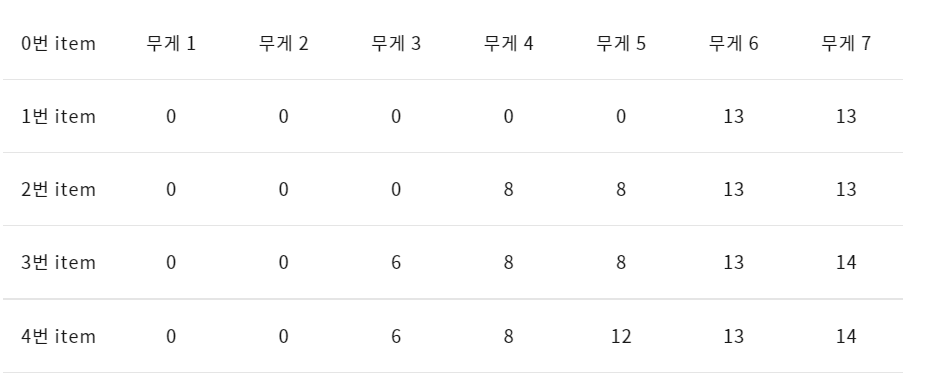
(출처 : https://fbtmdwhd33.tistory.com/60)
이 블로그에서 dp 테이블이 채워지는 과정을 잘 설명해두어서 이해하는데 도움이 많이 됐다!
코드로는 이렇게 표현할 수 있다.
for (int k = 1; k <= K; k++) { // 무게
for (int i = 1; i <= N; i++) { // item
dp[i][k] = dp[i - 1][k];
if (k - item[i][0] >= 0) {
dp[i][k] = Math.max(dp[i - 1][k], item[i][1] + dp[i - 1][k - item[i][0]]);
}
}
}코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] inputs = br.readLine().split(" ");
int N = Integer.parseInt(inputs[0]);
int K = Integer.parseInt(inputs[1]);
int[][] item = new int[N + 1][2]; // weight, value
for (int i = 1; i <= N; i++) {
inputs = br.readLine().split(" ");
item[i][0] = Integer.parseInt(inputs[0]);
item[i][1] = Integer.parseInt(inputs[1]);
}
int[][] dp = new int[N + 1][K + 1];
for (int k = 1; k <= K; k++) { // 무게
for (int i = 1; i <= N; i++) { // item
dp[i][k] = dp[i - 1][k];
if (k - item[i][0] >= 0) {
dp[i][k] = Math.max(dp[i - 1][k], item[i][1] + dp[i - 1][k - item[i][0]]);
}
}
}
System.out.println(dp[N][K]);
}
}
정리

✔ 알고리즘 분류 - 다이나믹 프로그래밍, 배낭 문제
✔ 난이도 - 🟡 Gold 5🤦♀️ 오늘의 메모
- 2학년 때 들었던 알고리즘 강의에서 분명히 했던 내용같은데
Knapsack algorithm이라는 용어만 익숙할 뿐 개념은 정말로 처음보는 것 같은.. 내용이었다. dp테이블에 값을 넣는 방법을 이해하는 데에 시간이 정말 오래 걸렸다..ㅠ Knapsack 알고리즘은 위키백과에 따르면 다음과 같다.
배낭 문제는 조합 최적화의 유명한 문제이다.
간단하게 말하면, 한 여행가가 가지고 가는 배낭에 담을 수 있는 무게의 최댓값이 정해져 있고
일정 가치와 무게가 있는 짐들을 배낭에 넣을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제이다.- 쪼갤 수 없는 짐이라면 dp를 사용해서 풀이한다. dp 테이블을 작성하는 원리를 잘 기억해둘 것!
