1. RB Tree란?
정의
Balanced binary search tree
RB Tree는 이진트리의 구조를 그대로 채용하되, 딱 하나 색상(Color)라는 속성을 노드에 추가함으로서 자동으로 균형을 잡는 알고리즘
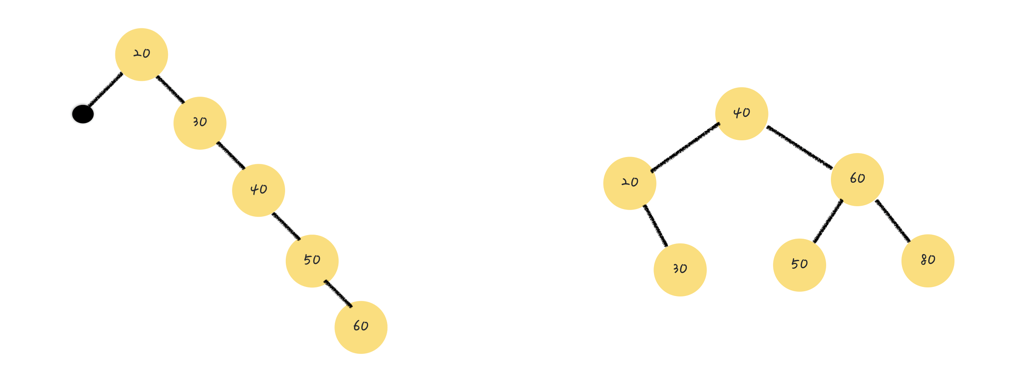
[Not balanced]
- search연산 :
O(h) (h=트리의높이)
[Balanced]
- search연산 :
O(logn)
2. RB Tree의 조건
레드블랙트리는 4개의 조건을 가지고있다.
Root Property: 루트노드의 색깔은 검정(Black)이다.External Property: 모든 external node들은 검정(Black)이다.Internal Property: 빨강(Red)노드의 자식은 검정(Black)이다. ==No Double Red(빨간색 노드가 연속으로 나올 수 없다.)Depth Property: 모든 리프노드에서 Black Depth는 같다. == 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙노드의 개수는 같다. (그냥 노드의 수는 다를 수 있음.)
3. 삽입/삭제
Ex1) 2, 8, 3 삽입
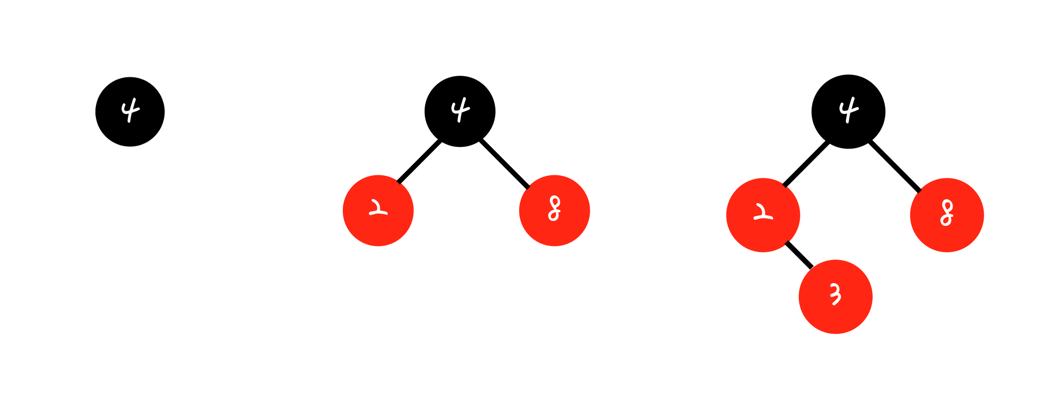
이 경우, 3번 조건(Internal Property)를 위반한다. (Red의 자식은 Black이어야하는데 Red==Double Red)
=> 해결법 ?
1. Restructuring
2. Recoloring
4. Restructuring / Recoloring

Double Red를 해결하는 방법은 현재 insert된 노드의 uncle node(부모의 형제 노드)의 색깔에 따라 수행하는 프로시저가 다르다.
즉 위 그림으로 따지면, 현재 insert된 노드 z의 uncle node는?
- 내 부모(v)의 형제(w)니
w가 된다
w가 검정(Black) 일 땐 Restructuring,
w가 빨강(Red) 일 땐 Recoloring을 수행한다.
Restructuring
- 나(z)와 내 부모(v), 내 부모의 부모(Grand Parent)를 오름차순으로 정렬
- 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
- 올라간 가운데 있는 값을 검정(Black)으로 만들고 그 두자식들을 빨강(Red)로 만든다.

- Restructuring은 다른 서브트리에 영향을 끼치지 않기 때문에 한번의 Restructuring이면 끝난다.
- 여기서 말하는 영향이란
Black Depth(조건 4번 : 모든 리프노드에서 Black Depth는 같다) - 즉, Double Red를 해결하기 전과 해결 한 후의 Black 노드의 개수에 변화가 없기때문에 다른서브트리에 영향을 끼치지 않게된다.
시간복잡도
Restructuring자체의 시간복잡도는 O(1)에 끝나지만, (순서결정시간 - 상수시간, 트리로 만드는시간 - 상수시간, 원래있던 노드들의 구조들을 바꿔주는 시간 - 상수시간)
Restructuring은 어떤 노드를 insertion한 뒤 일어나므로 총 수행시간은 O(logn)이다. (지금 현재 노드가 들어갈 위치를 먼저 찾아야 하기 때문)
Recoloring
- 현재 inset된 노드(z)의 부모와 그 형제(w)를 검정(Black)으로 하고 Grand Parent(내 부모의 부모)를 빨강(Red)로 한다.
- Grand Parent(내 부모의 부모)가 Root node가 아니었을 시 Double Red가 다시 발생 할 수 있다.
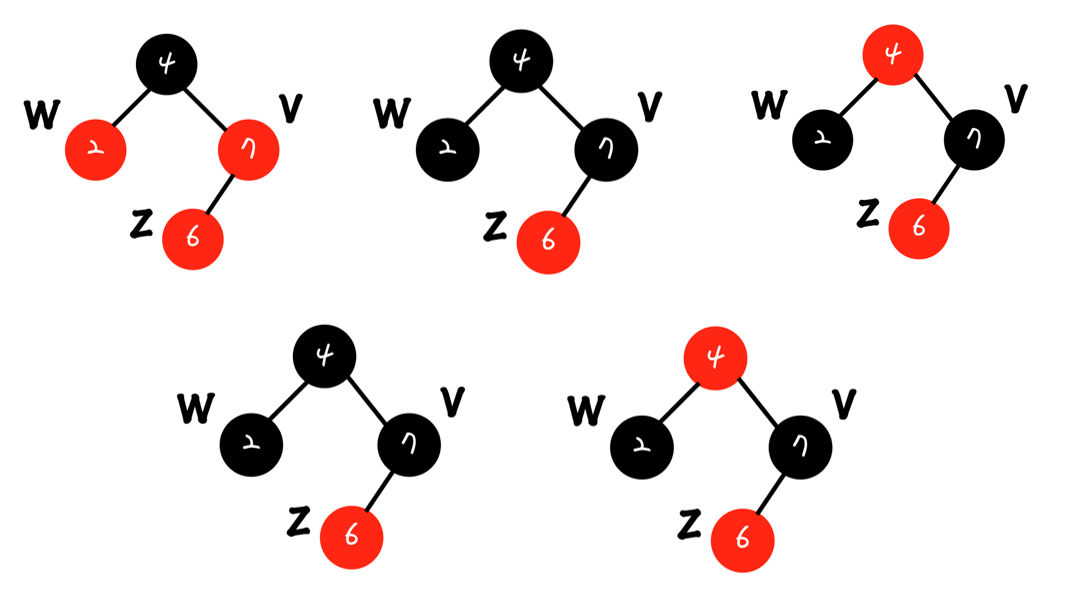
2번 그림) 현재 insert된 노드 z의 부모 (v) = 7과, 그 형제 (w) = 2의 색깔을 검정으로 만들어준다.
3번 그림) z의 Grand Parent를 빨강(Red)로 만들어준다.
4번 그림) 하지만, 만약 Grand Parent(내 부모의 부모)가 Root Node였다면, RB Tree의 1번조건(Root Property)에 의해 검정(Black)이 된다.
5번 그림) 알고보니까 지금 우리가 보는 트리가 어떤 큰 트리의 서브트리였고, 4라는 Key를 가진노드가 Root가 아니었다면 => Double Red가 생긴다.
- 한번에 안끝날 가능성이 있다. (최악의경우 Root까지 Recoloring 된다.)
의문이 들 수 있다
Q : 저렇게 막 내 부모랑 uncle노드를 막 검정으로 바꿔도돼??!!
레드블랙트리의 4번조건: Depth Property 만족해?
A : 네. 만족합니다. Black Depth는 일제히 1증가하기 때문에 문제가 없습니다시간복잡도
insert를 하는데 "내 위치"를 찾아야한다. => O(logn)
Restructuring과 마찬가지로 Recoloring은 O(1)의 시간이 걸립니다.
하지만, Recoloring은 Root까지 propagation될 수 있으므로 최악의 경우 O(logn)이 걸리게 된다.
=> 총 O(logn)
5. 활용 분야
- 레드-블랙 트리는 자료의 삽입과 삭제, 검색에서 최악의 경우에도 일정한 실행 시간을 보장한다. 이는 실시간 처리와 같은 실행시간이 중요한 경우에 유용하게 쓰일 뿐만 아니라, 일정한 실행 시간을 보장하는 또 다른 자료구조를 만드는 데에도 쓸모가 있다. 예를 들면, 각종 기하학 계산에 쓰이는 많은 자료 구조들이 레드-블랙 트리를 기반으로 만들어져 있다.
- Java의 Collection에서 ArrayList의 내부적인 알고리즘이 RBT로 이루어져 있음.
