[자료구조] Stack, Queue

Stack

LIFO (Last In First Out, 후입선출)
=> 가장 나중에 들어온 것이 가장 먼저 나옴

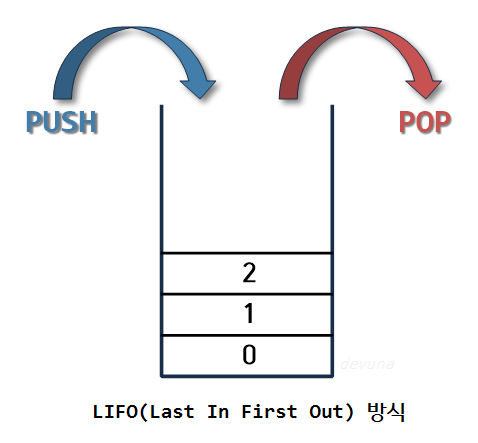
(이미지 출처 : https://devuna.tistory.com/22)

스택의 활용 예시

스택의 특징인 후입선출(LIFO)을 활용하여 여러 분야에서 활용 가능하다.

• 웹 브라우저 방문기록 (뒤로 가기) : 가장 나중에 열린 페이지부터 다시 보여준다.
• 역순 문자열 만들기 : 가장 나중에 입력된 문자부터 출력한다.
• 실행 취소 (undo) : 가장 나중에 실행된 것부터 실행을 취소한다.
• 후위 표기법 계산
• 수식의 괄호 검사 (연산자 우선순위 표현을 위한 괄호 검사)

스택의 기능(함수)

- SP : Stack Pointer
- push() : 데이터 넣음
- pop() : 데이터 최상위 값 뺌
- isEmpty() : 비어있는 지 확인
- isFull() : 꽉차있는 지 확인

SP(Stack Pointer)

push와 pop할 때는 해당 위치를 알고 있어야 하므로, 기억하고 있는 스택 포인터(SP)가 필요하다.

private int sp = -1; //처음 기본값은 -1

push()

public void push(Object o) {
    if(isFull(o)) { // 스택 포인터가 최대 크기와 같으면 return
        return;
    }
    
    // 아니면 스택의 최상위 위치에 값을 넣음
    stack[++sp] = o;
}

pop()

public Object pop() {
    
    if(isEmpty(sp)) { // 스택 포인터가 0이 되면 null로 return;
        return null;
    }
    
    Object o = stack[sp--]; // 아니면 스택의 최상위 위치 값을 꺼내옴
    return o;
    
}

isEmpty()

private boolean isEmpty(int cnt) {
    // 입력 값이 최초 값과 같다면 true, 아니면 false
    return sp == -1 ? true : false; 
}

isFull()

private boolean isFull(int cnt) {
    // 스택 포인터 값+1이 MAX_SIZE와 같으면 true, 아니면 false
    return sp + 1 == MAX_SIZE ? true : false; 
}

Queue

FIFO (First In First Out, 선입선출)
=>가장 먼저 들어온 것이 가장 먼저 나옴

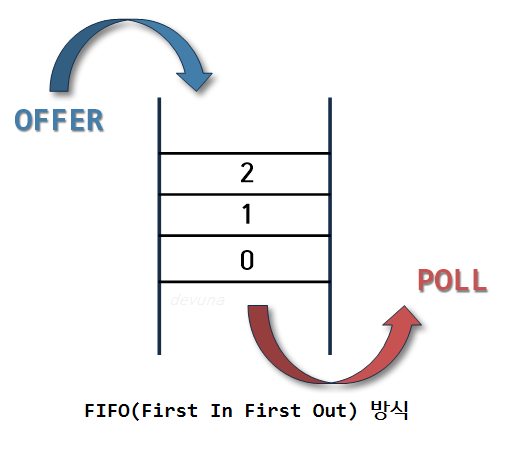
(이미지 출처 : https://devuna.tistory.com/22)

큐의 활용 예시

큐는 주로 데이터가 입력된 시간 순서대로 처리해야 할 필요가 있는 상황에 이용한다.

• 우선순위가 같은 작업 예약 (프린터의 인쇄 대기열)
• 은행 업무
• 콜센터 고객 대기시간
• 프로세스 관리
• 너비 우선 탐색(BFS, Breadth-First Search) 구현
• 캐시(Cache) 구현

큐의 기능(함수)

enQueue() : 데이터 넣음
deQueue() : 데이터 뺌
isEmpty() : 비어있는 지 확인
isFull(): 꽉차있는 지 확인 

front : deQueue 할 위치 기억
rear : enQueue 할 위치 기억

기본 값

private int size = 0; 
private int rear = -1; 	// 초기값 -1
private int front = -1; // 초기값 -1

Queue(int size) { 
    this.size = size;
    this.queue = new Object[size];
}

enQueue

public void enQueue(Object o) {
    
    if(isFull()) { //enQueue 시, 가득 찼다면 꽉 차 있는 상태에서 enQueue를 했기 때문에 overflow

        return;
    }
    
    queue[++rear] = o; // 아니면 rear에 값 넣고 1 증가
}

deQueue

public Object deQueue(Object o) {
    
    if(isEmpty()) { // deQueue를 할 때 공백이면 underflow
        return null;
    }
    
    Object o = queue[front]; 	// front에 위치한 값을 object에 꺼낸 후,
    queue[front++] = null; 	// 꺼낸 위치는 null로 채워줌
    return o;
}

isEmpty

public boolean isEmpty() {
    return front == rear; // front와 rear가 같아지면 비어진 것
}

isFull

public boolean isFull() {
    return (rear == queueSize-1);
}

일반 큐의 단점

큐에 빈 메모리가 남아 있어도, 꽉 차있는것으로 판단할 수도 있다. (rear가 끝에 도달했을 때)

=> 이를 개선한 것이 원형 큐 : 논리적으로 배열의 처음과 끝이 연결되어 있는 것으로 간주한다!

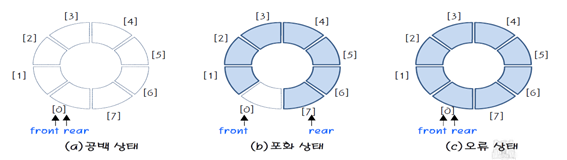
(이미지 출처 : https://blog.daum.net/lkno01/67)

• 원형 큐는 초기 공백 상태일 때 front와 rear가 0
• 공백, 포화 상태를 쉽게 구분하기 위해 자리 하나를 항상 비워둠
• (index + 1) % size로 순환시킨다

출처

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Computer%20Science/Data%20Structure/Stack%20%26%20Queue.md#%EA%B8%B0%EB%B3%B8%EA%B0%92
https://devuna.tistory.com/22