최장 증가 부분 수열(LIS)

최장 증가 부분 수열이란?

컴퓨터 공학에서, 최장 증가 부분 수열 문제는, 주어진 수열에서 오름차순으로 정렬된 가장 긴 부분수열을 찾는 문제이다.
-위키백과

위와같은 수열 A가 주어졌을 때, 몇 개의 수를 제거해 부분수열을 만들 수 있다.

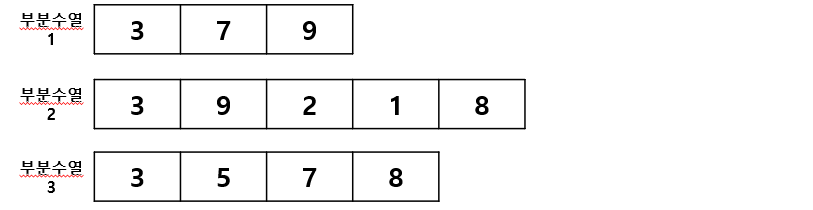이런 부분 수열 중, 길이기 가장 긴 수열을 최장 증가 부분 수열 이라고 한다.
위의 예시중, 부분수열 3이 수열 A의 최장 증가 부분 수열이다.

풀이 1. DP - O(N^2)

풀이 방법

1. 수열 A의 길이와 같은 크기의 DP 배열을 선언한다.
2. DP배열 각 idx의 값은 idx까지의 부분 수열 중 가장 긴 부분 수열의 길이 의미한다.
3. 이중 반복문을 이용한다.
   3-1. 첫번째 반복문은 부분 수열의 종료 지점을 설정한다.
   3-2. 두번째 반복문은 3-1.을 통해 분리한 부분 수열 중 가장 긴 부분 수열을 계산한다.
   3-3. DP[end] = max(DP[end], DP[i] + 1)

코드

nums = list(map(int, input().split())) 
# 1. 수열 A의 길이와 같은 크기의 DP 배열을 선언한다.
LIS = [1 for _ in range(N)] 
# 3-1. 첫번째 반복문은 부분 수열의 종료 지점을 설정한다.
for end in range(N):
    # 3-2. 두번째 반복문은 3-1.을 통해 분리한 부분 수열 중 가장 긴 부분 수열을 계산한다.
    for i in range(end + 1):
        if nums[end] > nums[i]: # 수열의 i번째 값보다 end번째 값이 더 크다면, 증가 부분 수열이 될 수 있다.
            LIS[end] = max(LIS[end], LIS[i]+1) # LIS[i]+1 : i번째 까지의 LIS에 end번째 수열을 추가했을 때의 길이
print(max(LIS))

풀이 2. 이분탐색 - O(NlogN)

이전의 원소들을 탐색하는 과정을 이분탐색(lower bound)를 이용하여 시간을 줄이는 방법이다.
이 때 DP[length]는 길이가 length인 증가 부분수열들 중 마지막이 가장 작은 값으로 정의한다.
DP[length]의 값을 가장 작은 값으로 정의하는 이유는 다음과 같다.
수열이 주어지고, ?, ? 는 무슨 값이 있을지 아직 탐색하지 않은 상태일때

• 길이가 2인 증가 부분 수열은 {7, 9}와 {1, 2}이다.
• 길이가 3인 증가 부분 수열을 만들기 위해서는
  - {1, 2}의 경우 3이상의 어떤 수가 와도 가능하다.
  - {7, 9}의 경우 10이상의 어떤 수가 와도 가능하다.
• {1, 2}의 부분수열의 경우 가능한 숫자가 더 많으므로 맨 마지막값을 최소로 유지해야 한다.

풀이 방법

1. 반복문을 이용하여 주어진 순열을 순서대로 탐색한다.
2. LIS의 길이 l을 0에서 시작하여
   2-1. DP[l] > 순열[현재 탐색]의 경우 DP[l+1]에 현재 값을 추가한다.
   2-2. DP[l] <= 순열[현재 탐색]의 경우, 이분탐색을 통해 DP안의 값 중 현재 탐색중인 값의 lower_bound를 찾아 swap한다.
3. 최종적으로 나온 DP의 크기가 LIS의 크기이다.
4. DP를 통해 얻은 수열은 LIS가 아닐 수 있다.

코드

# lower bound는 데이터내 특정 K값보다 같거나 큰값이 처음 나오는 위치를 리턴
def lower_bound(left, right, val):
    while (left < right):
        mid = (left + right) // 2
        if val <= DP[mid]:
            # {1, 2, 2, 3, 3} 의 수열에서 3의 lower_bound는 idx = 3이다.
            # 따라서 같은 경우도 범위를 좁혀나간다.
            right = mid
        else:
            left = mid + 1
    return left


nums = {3, 5, 7, 9, 2, 1, 4, 8}
DP = [-1]
length = 0
for n in nums:
    if n > DP[length]:
        DP.append(n)
        length += 1
    elif n < DP[length]:
        lb = lower_bound(0, length, n)
        DP[lb] = n

print(len(DP)-1)

풀이 3. 세그먼트 트리 - O(NlogN)

세그먼트 트리는 특정한 범위의 정보를 저장하는데 사용되는 트리 데이터 구조이다.
세그먼트 트리 노드들은 구간의 최대 LIS길이를 저장하게 한다면 root에서 모든 구간의 최대 LIS길이를 구할 수 있다.
세그먼트 트리를 이용한다면 구간에서의 LIS길이 최댓값을 찾는데 시간을 O(logN)을 사용할 수 있다.

< LIS 구할 때, 세그먼트 트리 초기 상태 >

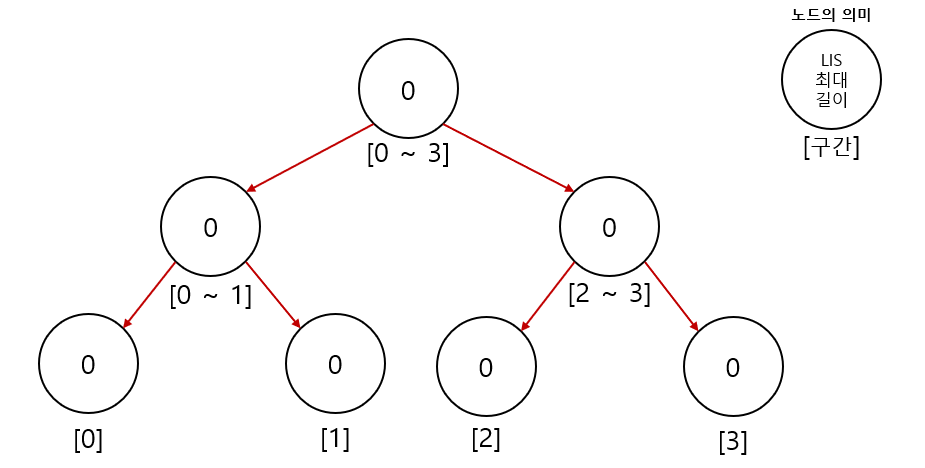
풀이 방법

수열 A가 위와 같이 주어질때, 세그먼트 트리를 이용한 풀이방법은 다음과 같다.

1. 수열 A를 인덱스 정보를 갖고있는 상태로, val를 기준으로 오름차순 정렬, 같은 경우 idx 기준 내림차순으로 정렬한 배열을 만든다.각 배열의 값은 수열 A의 (val, idx) 를 의미한다.
2. 배열 B의 순서대로 세그먼트 트리를 만들어 나간다. B는 탐색 순서를 위한 배열이다.
   이 때, 각 구간은 B가 아닌 A의 인덱스를 의미한다.
   2-1. B[0] = (1, 1) 확인
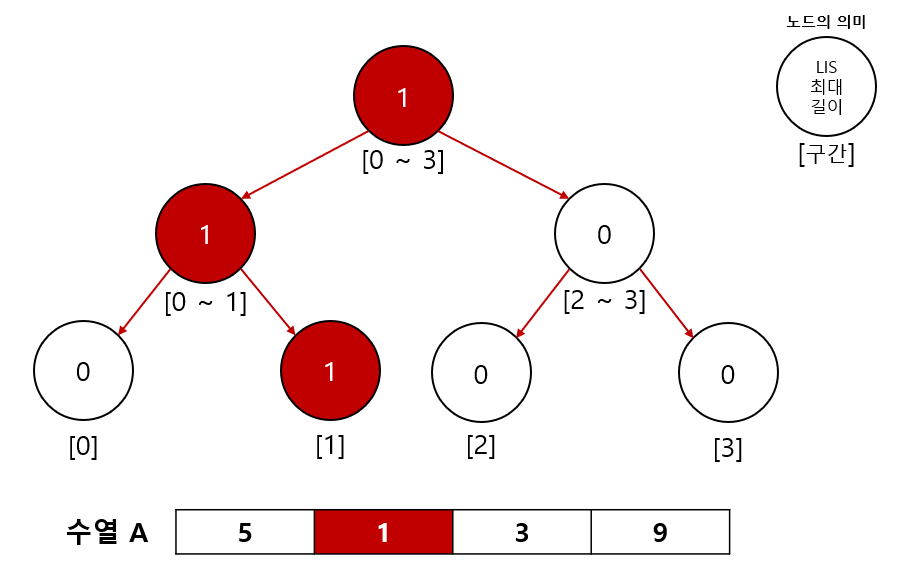
   B[0]의 값 1은 A의 인덱스 1번에 위치해 있었으므로 A의 [0 ~ 0]구간의 최댓값을 확인한다. 해당 구간에서의 최댓값은 0이므로 1을 업데이트 한다.
   2-2. B[1] = (3, 2) 확인
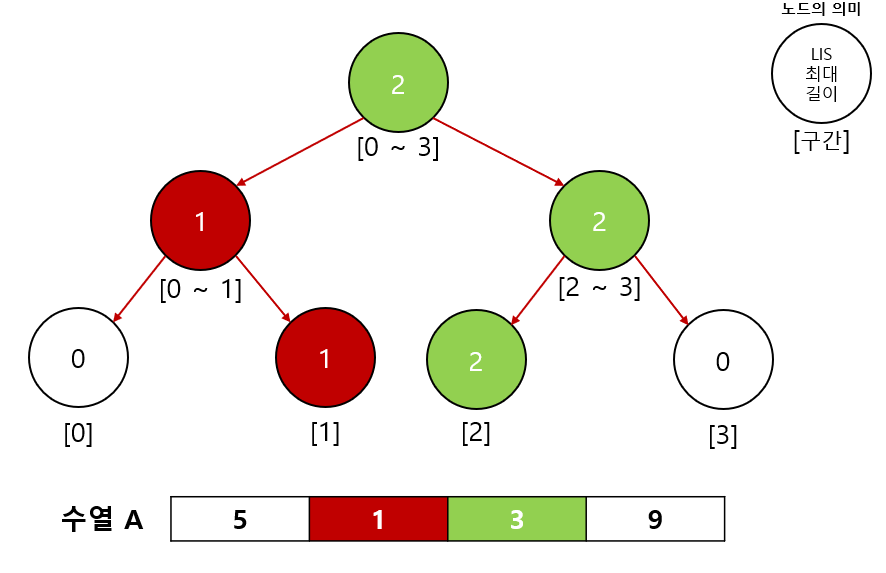
   B[1]의 값 3은 A의 인덱스 2번에 위치해 있었으므로 A의 [0 ~ 1]구간의 최댓값을 확인한다. 해당 구간의 최댓값은 1이므로 2를 업데이트 한다.
   2-3. B[2] = (5, 0) 확인
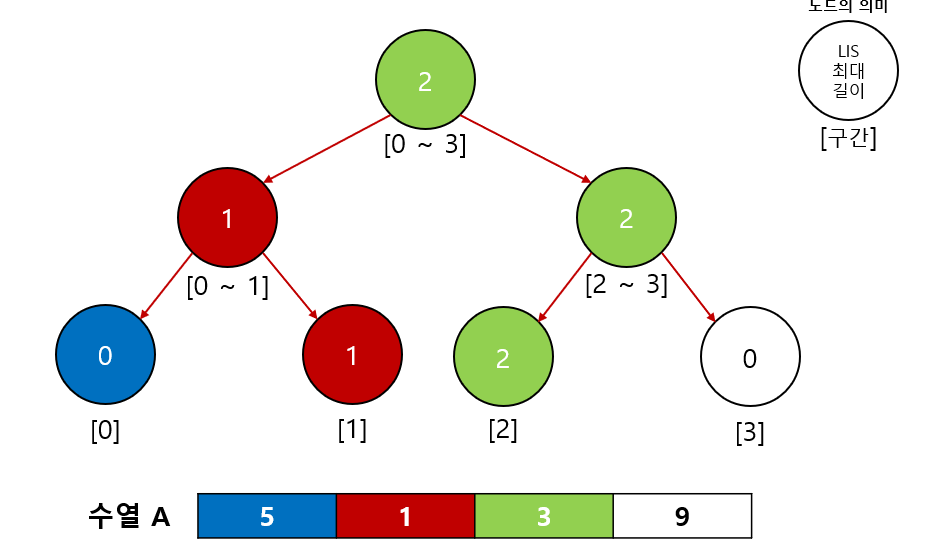
   B[2]의 값 5는 A의 인덱스 0번에 위치해 있었으므로 A의 [0 ~ 0] 구간의 최댓값을 확인한다. 1을 업데이트 한다.
   2-4. B[3] = (9, 3) 확인
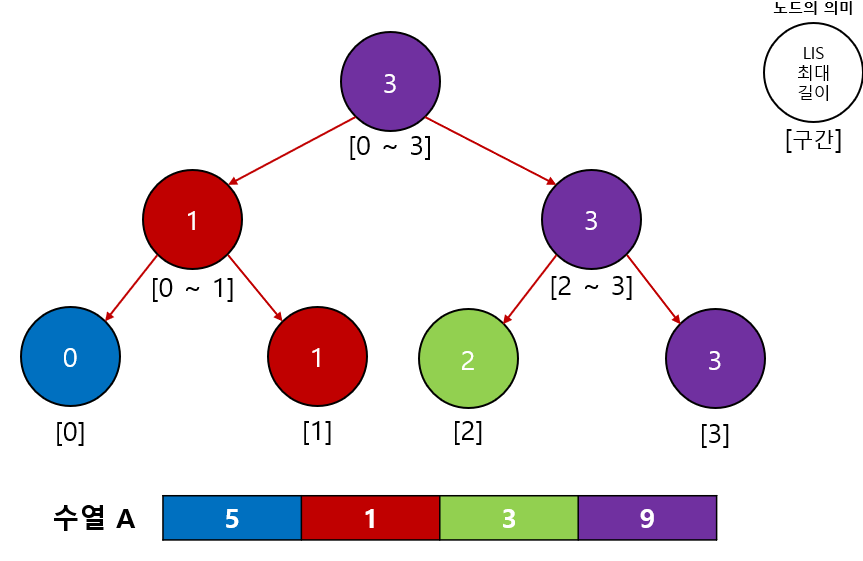
   B[3]의 값 9는 A의 인덱스 3번에 위치해 있었으므로 A의 [0 ~ 2] 구간의 최댓값을 확인한다. 최댓값은 2이므로 3을 업데이트 한다.
3. 최종적으로 root의 값이 LIS의 길이다.

A의 값을 오름차순으로 정렬한 배열 B를 이용하여 하는 이유

A[i]가 A[0 ~ i]의 어떤 값과 연결되어 LIS가 되기 위해서는 적어도 연결되는 값보다는 커야한다.
A를 정렬한 배열 B를 사용한다면 이전 탐색보다 항상 큰 값을 확인하기 때문에 이전 탐색으로 완성한 [0 ~ i]구간 LIS의 마지막 값보다 큰것이 보장될 수 있기 때문이다.

코드

  def find_max_val(node_id, start, end, left, right):
    '''
    :param node_id: 트리의 노드 id 
    :param start: 트리 탐색 시작 지점
    :param end: 트리 탐색 종료 지점
    :param left: 찾고자 하는 구간 시작 지점
    :param right: 찾고자 하는 구간 종료 지점
    :return: 찾고자 하는 구간의 최댓값
    '''
    # 범위 밖이면 0을 반환, 재귀가 반복될 수록 end 는 줄어들고 start는 커지므로 범위체크를 한다.
    if left > end or right < start:
        return 0
    # 범위 안이면 현재 값 반환
    if left <= start and end <= right:
        return tree[node_id]
    mid = (start + end) // 2
    ret = max(find_max_val(node_id * 2 + 1, start, mid, left, right),
              find_max_val(node_id * 2 + 2, mid + 1, end, left, right))
    return ret


def update(node_id, start, end, idx, val):
    '''
    :param node_id: 트리의 노드 id
    :param start: 트리 탐색 시작 지점
    :param end: 트리 탐색 종료 지점
    :param idx: 변경할 인덱스
    :param val: 변경할 값
    '''
    if idx > end or idx < start:
        return
    if start == end:
        tree[node_id] = val
        return

    mid = (start + end) // 2
    update(node_id * 2 + 1, start, mid, idx, val)
    update(node_id * 2 + 2, mid + 1, end, idx, val)

    tree[node_id] = max(tree[node_id * 2 + 1], tree[node_id * 2 + 2])


#N = int(input())
#nums = list(map(int, input().split()))
N = 8
nums = [3, 5, 7, 9, 2, 1, 4, 8]
tree = [0] * 4000000 # 4를 곱하면 모든 범위를 커버할 수 있다. 트리는 2의 제곱형태의 길이를 갖는다.

s_nums = [(v, i) for i, v in enumerate(nums)]
s_nums.sort(key = lambda x: (x[0], -x[1])) # val기준으로 정렬, val이 같을 경우 idx 기준으로 정렬한다.

for val, idx in s_nums:
    max_val = find_max_val(0, 0, N - 1, 0, max(idx - 1, 0))
    update(0, 0, N - 1, idx, max_val + 1)

print(tree[0])

참고 사이트

풀이 2. 이분탐색 : https://loosie.tistory.com
풀이 3. 세그먼트 트리 : https://blog.naver.com/kks227