[자료구조] Binary Search Tree

이진 탐색 트리

이진트리 기반의 탐색을 위한 자료구조이다
이진트리의 크기는 left < root < right 조건을 따른다
모든 서브 트리에서 적용되는 조건이다

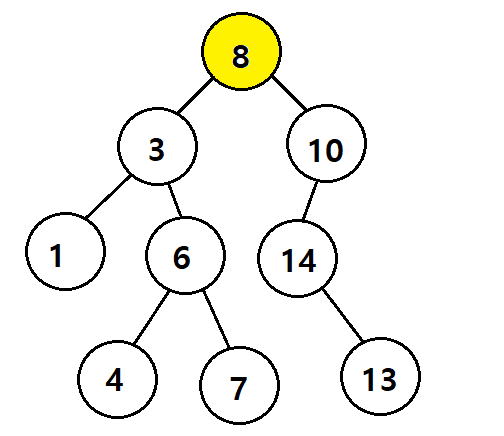
• 아래의 트리를 보면 root 8을 기준으로 서브 트리들이 왼쪽은 8보다 작고 오른쪽은 8보다 크다
  -> 각각의 트리들도 적용되는 기준이라 3을 기준으로 왼쪽이 3보다 작고 오른쪽은 3보다 크다
  

클래스 생성 & 초기화

• template로 클래스를 생성하여 메인함수에서 자료형을 지정할 것이다
• 이진탐색트리는 노드구조이기에 노드 구조체를 정의해준다
• 노드는 데이터, left포인터, right포인터로 구성
• root노드를 가리킬 포인터도 선언

#include <iostream>

using namespace std;

template <typename T>
class BinarySearchTree
{
private:
    struct Node
    {
        T data;

        Node* left;
        Node* right;
    };

    Node* root;
public:
    BinarySearchTree()
    {
        root = nullptr;
    }

---

Insert( ) 함수 : 원하는 데이터 삽입

void Insert(T data)
{
    if (root == nullptr)
    {
        root = CreateNode(data);
    }
    else
    {
        Node* currentNode = root;

        while (currentNode != nullptr)
        {
            if (currentNode->data == data)
            {
                return;
            }
            else if (currentNode->data > data)
            {
                if (currentNode->left == nullptr)
                {
                    currentNode->left = CreateNode(data);
                    break;
                }
                else
                {
                    currentNode = currentNode->left;
                }
            }
            else
            {
                if (currentNode->right == nullptr)
                {
                    currentNode->right = CreateNode(data);

                    break;
                }
                else
                {
                    currentNode = currentNode->right;
                }
            }
        }
    }
}
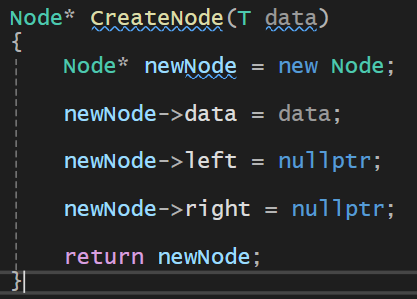
Node* CreateNode(T data)
{
    Node* newNode = new Node;

    newNode->data = data;

    newNode->left = nullptr;

    newNode->right = nullptr;

    return newNode;
}

1. 만약 root가 nullptr인 경우

-> root가 가리키는 곳이 없다는 건 트리가 비어있다는 상태
-> 노드를 하나 생성해주고 (CreateNode함수) 그 노드에 데이터를 삽입한다

2. 노드가 하나 이상 있는 경우

-> 현재 노드를 탐색 할 currentNode 포인터 생성 후 처음은 root노드를 가리킨다
-> currentNode가 가리키는 곳에 노드가 있다면 반복문 실행
-> currentNode가 가리키는 곳의 데이터가 내가 삽입하려는 데이터과 같으면 return

이진 탐색트리에서는 중복된 값을 허용하지 않는다!!
그렇기 때문에 바로 함수 탈출

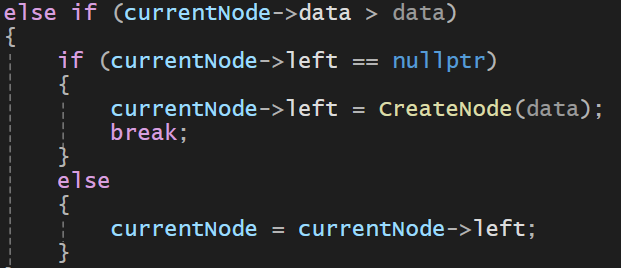
• -> 내가 넣으려는 값이 currentNode가 가리키는 값보다 작으면 왼쪽으로 계속 이동하거나 그 위치에 노드 생성 후 값을 넣어줘야한다

  만약 currentNode의 왼쪽자식이 nullptr이라면 왼쪽 자식에는 노드가 없는 것
  currentNode보다 값이 작으면서 왼쪽에 노드가 없으니 여기에 새 노드를 만들고 데이터 넣어준다
  

• -> 반대로 내가 넣으려는 값이 currentNode가 가리키는 값보다 크면 오른쪽으로 계속 이동하고, currentNode의 오른쪽 자식이 없을때까지 도달했다면 그 위치에 노드생성 후 데이터 삽입

  

노드가 하나 이상 있는 경우 예시)

• 내가 넣고 싶은 값은 13이고 현재 currentNode는 root인 8을 가리키고 있다
• 만약 내가 넣고싶은 값이 currentNode가 가리키는 값과 같으면 바로 return인데 13은 그렇지 않으니 다른 조건문으로 들어간다
  
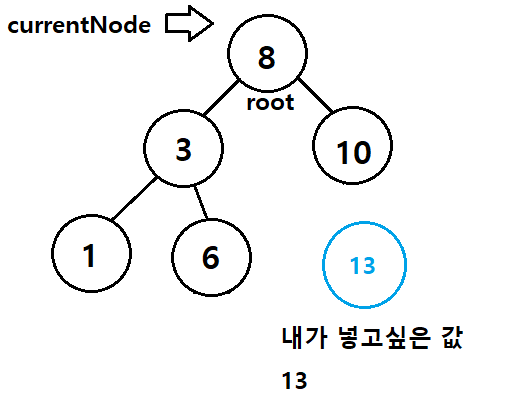
• 이 트리구조에서는 내가 넣고 싶은 값이 currentNode의 데이터 보다 큰 경우로 들어가야한다
• 그러니 currentNode의 right가 nullptr인 곳 까지 도달하면 거기에 노드 생성 후 데이터 삽입
  

---

Remove( ) 함수 : 원하는 데이터 삭제

과정:

• 탐색 : 내가 지우고자 하는 값을 찾기
  
  
• 만약 지우고자 하는 값을 찾지 못했을 경우 -> 찾지 못했다
  
  
• 만약 지우고자 하는 값을 찾은 경우
  -> 1. 지우고 싶은 값의 자식이 2개 다 없는 경우
  -> 2. 지우고 싶은 값의 자식이 1개만 있는 경우
  -> 3. 지우고 싶은 값의 자식이 2개 다 있는 경우

매개변수로 내가 지우고 싶은 data의 값이 들어온다

void Remove(T data)
{
    if (root == nullptr)
    {
        cout << "Binary Search Tree is Empty" << endl;
    }
    else
    {
        Node* currentNode = root;
        Node* parentNode = nullptr;

        while (currentNode != nullptr && currentNode->data != data)
        {
            if (currentNode->data > data)
            {
                parentNode = currentNode;
                currentNode = currentNode->left;
            }
            else
            {
                parentNode = currentNode;
                currentNode = currentNode->right;
            }
        }

        if (currentNode == nullptr)
        {
            cout << "Data Not found in the Binary Search Tree" << endl;
        }
        else if (currentNode->left == nullptr && currentNode->right == nullptr)
        {
            if (parentNode != nullptr)
            {
                if (parentNode->left == currentNode)
                {
                    parentNode->left = nullptr;
                }
                else
                {
                    parentNode->right = nullptr;
                }
            }
            else
            {
                root = nullptr;
            }
        }
        else if (currentNode->left == nullptr || currentNode->right == nullptr)
        {
            Node* childNode = nullptr;

            if (currentNode->left != nullptr)
            {
                childNode = currentNode->left;
            }
            else
            {
                childNode = currentNode->right;
            }

            if (parentNode != nullptr)
            {
                if (parentNode->left == currentNode)
                {
                    parentNode->left = childNode;
                }
                else
                {
                    parentNode->right = childNode;
                }
            }
        }
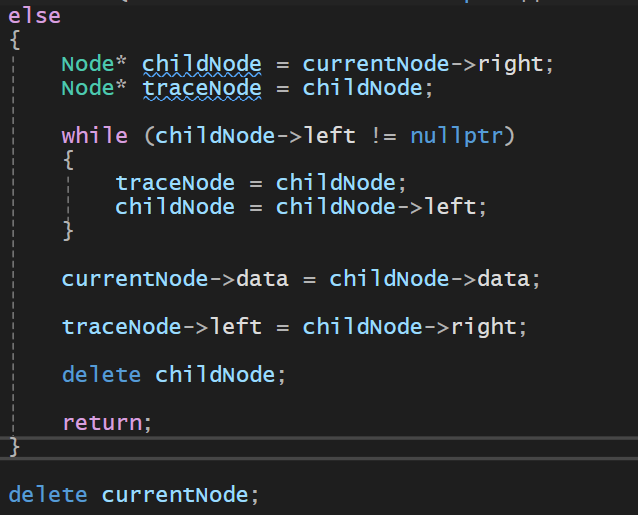
        else
        {
            Node* childNode = currentNode->right;
            Node* traceNode = childNode;

            while (childNode->left != nullptr)
            {
                traceNode = childNode;
                childNode = childNode->left;
            }

            currentNode->data = childNode->data;

            traceNode->left = childNode->right;

            delete childNode;

            return;
        }

        delete currentNode;

    }
}

Remove 탐색

root가 nullptr인 경우

• root가 nullptr이면 가리키고 있는 노드가 없는 것이므로 트리가 비어있는 구조

root가 nullptr이 아니라면 노드가 있는 것

• 노드를 탐색해 줄 currentNode 포인터 생성

• currentNode의 부모노드를 가리키는 parentNode포인터 생성

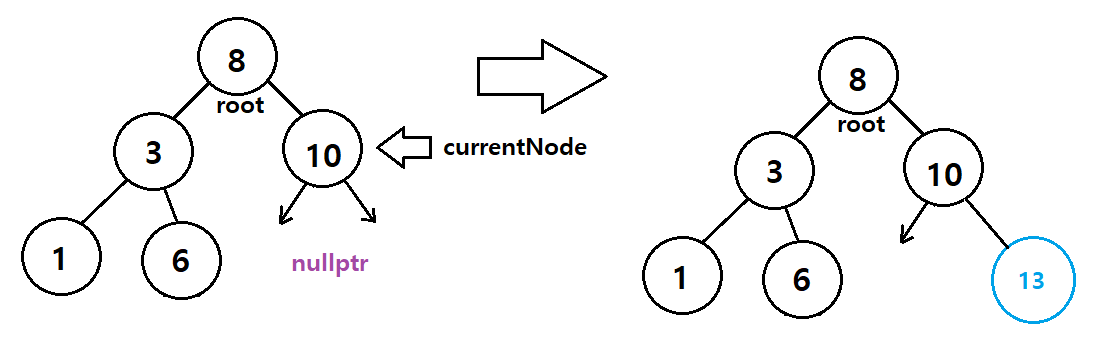
• 노드가 있지만, currentNode가 가리키는 값이 내가 원하는 값이 아니라면 currentNode와 parentNode의 이동이 필요하다

• currentNode와 parent노드의 이동은 사진과 같다

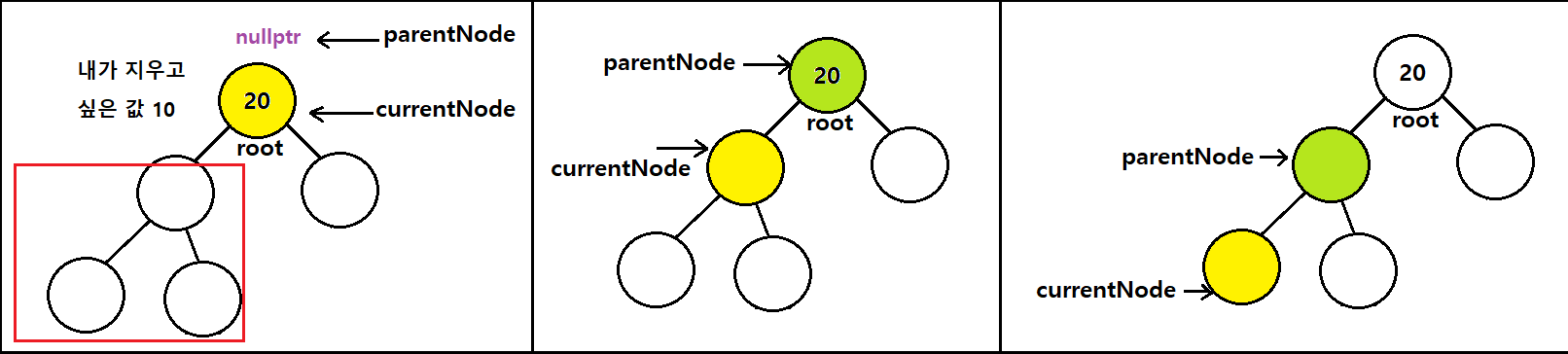
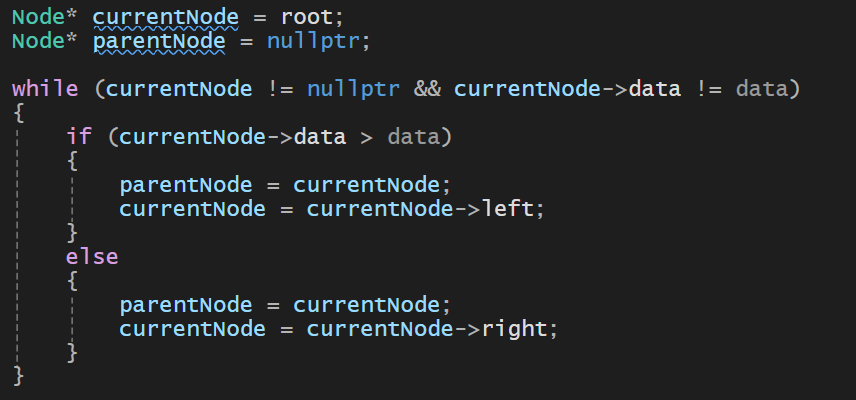
지우고자 하는 값을 못찾은 경우

• 위의 while문을 다 돌아서 현재 노드가 nullptr이 되었는데도 값을 찾지 못한 것임

  

지우고자 하는 값을 찾은 경우 -> 자식이 2개 다 없는 경우

아래에 자식이 없으면 바로 parentNode에서 처리해주면 된다 (다른 처리는 필요없음)

• 지우고자 하는 값이 currentNode가 가리키는 곳이고 그의 부모가 parentNode가 가리키는 곳이다

• 여기서 조건문 if(parentNode != nullptr)은 parentNode 즉, 현재 가리키는 노드는 부모가 있기에 root 노드가 아니라는 소리이다

• 1. 만약 parentNode의 왼쪽 자식이 현재 가리키는 currentNode라면 왼쪽을 nullptr로 만들어주기
• 2. 만약 parentNode의 오른쪽 자식이 현재 가리키는 currentNode라면 오른쪽을 nullptr로
• 3. 만약 parentNode가 nullptr이라면 현재 노드가 가리키고 있는 곳이 root인것이니 root를 nullptr로 해주면 된다
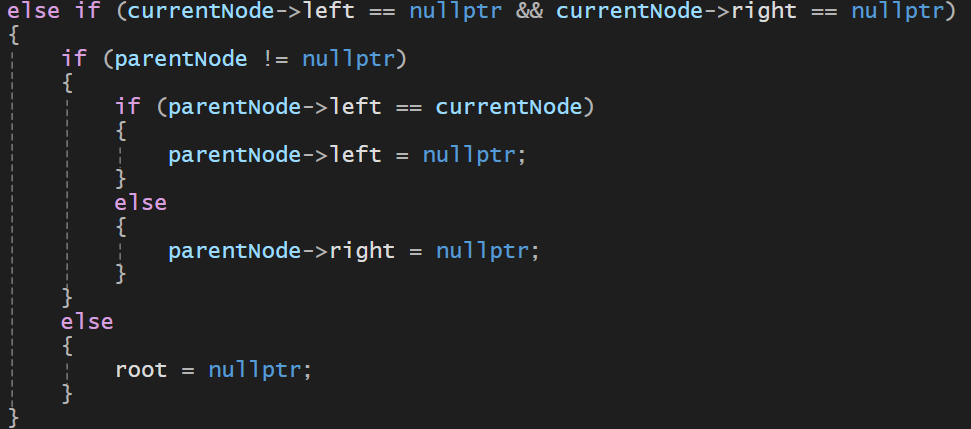
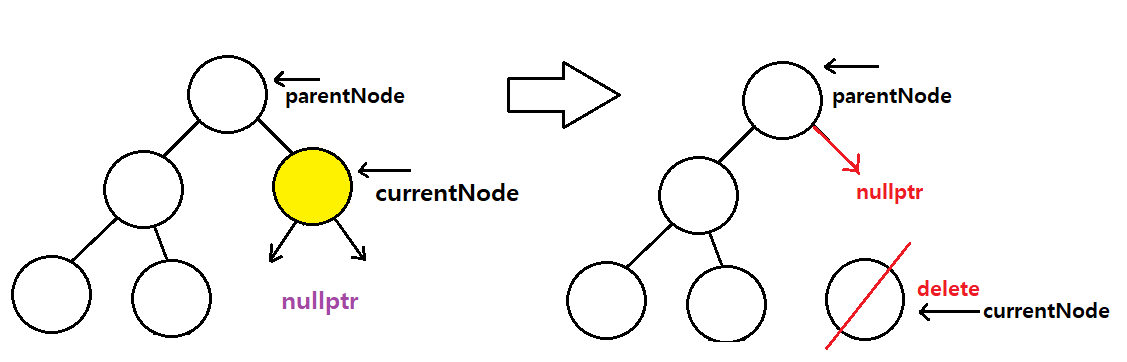
• 4. 마지막으로 currentNode가 가리키는 곳을 해제
     
     

지우고자 하는 값을 찾은 경우 -> 자식이 1개만 있는 경우

• 내가 지우고자 하는 곳이 currentNode가 가리키는 곳이고 자식이 왼쪽이나 오른쪽 , 둘 중 하나만 있는 경우이다
• currentNode의 왼쪽이나 오른쪽의 노드가 있을 경우 그 노드를 childNode가 가리키게 함
• parentNode가 가리키는 노드가 있고 그 노드가 currentNode라면 가리키는 노드를 child노드로 바꿔준다
• 마지막에 currentNode를 해제
  
  

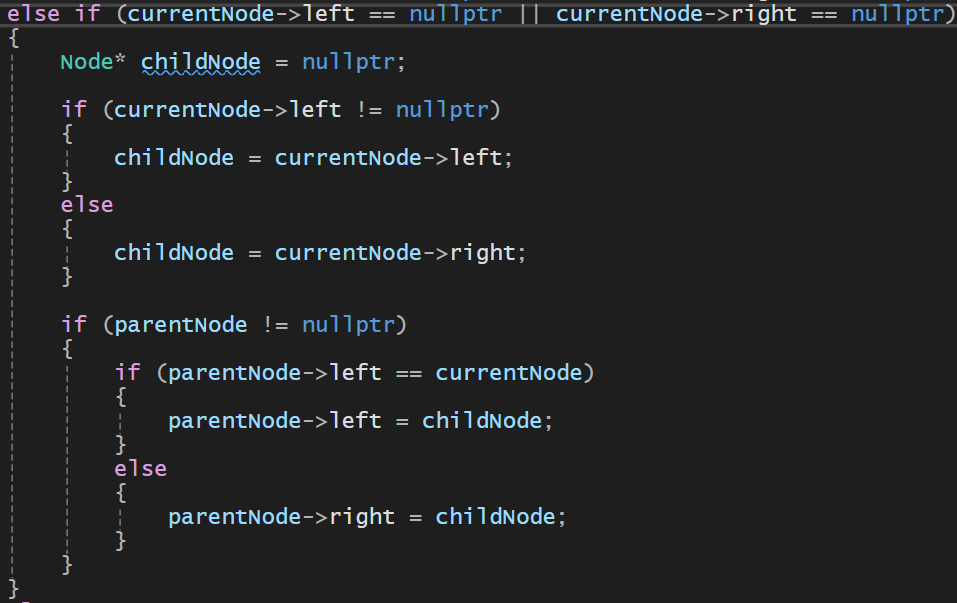
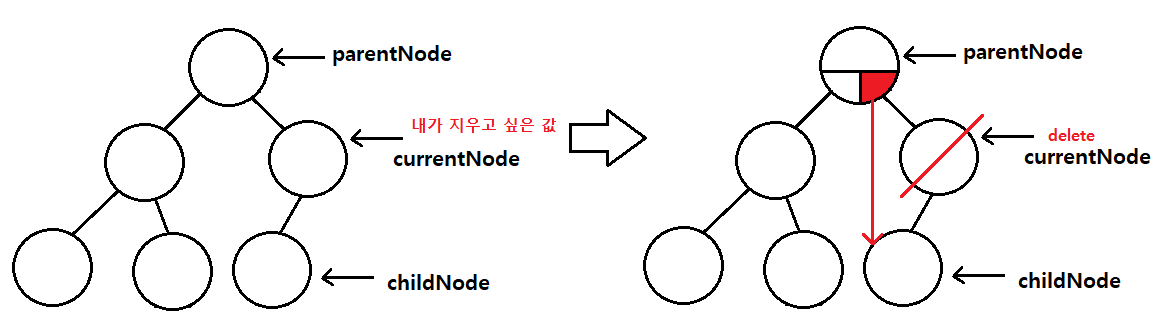
지우고자 하는 값을 찾은 경우 -> 자식이 2개 다 있는 경우

• 자식이 2개 다 있는 경우에 바로 currentNode를 삭제하게 되면 트리구조의 특징을 만족할 수 없다
• 트리구조를 만족하기 위해서는 반드시 값이 left < root < right가 되야한다
• currentNode의 오른쪽 값을 childNode로 지정하고 traceNode도 childNode를 가리킨다

삭제하고 싶은 노드를 기준으로 오른쪽 서브 트리들(root보다 큰 값들) 중 가장 작은 값을 찾아야한다

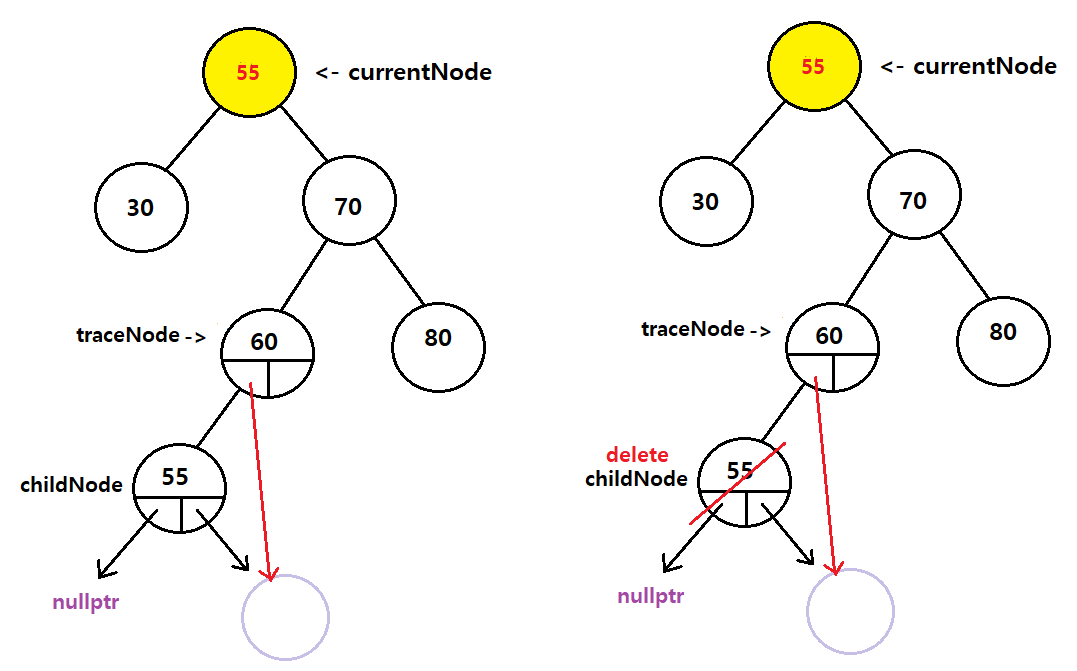
1. 삭제하고 싶은 노드를 가리키는 currentNode와 currentNode의 오른쪽 자식을 가리키는 childNode와 childNode를 가리키는 traceNode

2. childNode의 left가 nullptr이 될때까지 이동
-> 즉, childNode가 삭제하고픈 노드 기준, 오른쪽에서 가장 작은 값 까지 이동

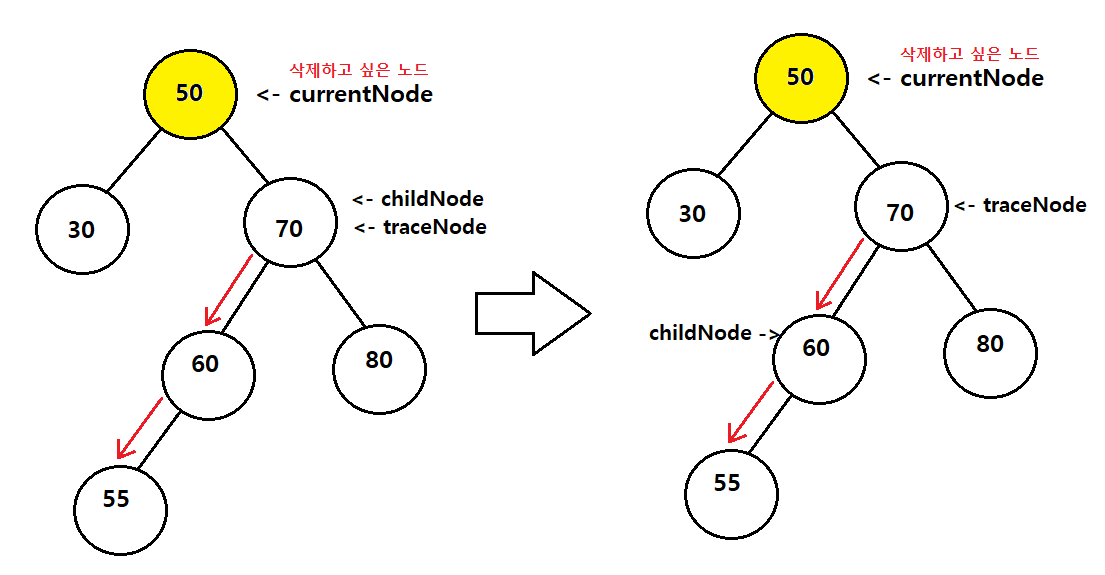
3. 가장 작은 값인 55를 찾고 55를 childNode가 가리킨다

4. traceNode는 childNode의 부모인 60을 가리키고 있다

5. childNode의 값을 currentNode에 대입한다


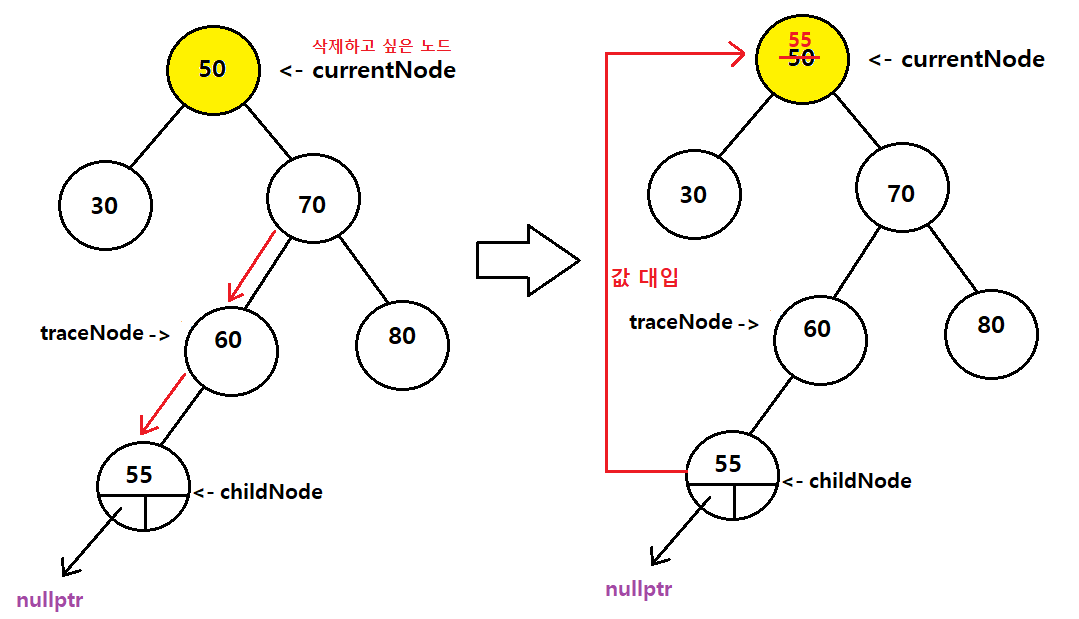
6. traceNode의 left가 childNode의 오른쪽 자식을 가리킨다

child의 왼쪽자식은 nullptr이 맞다
-> 이유 : childNode가 가장 작은 값까지 도달했기 때문에 그 밑에 자식은 당연히 없다
-> 하지만 childNode의 오른쪽 자식은 있을 수도 있고 없을 수도 있기 때문에 traceNode를 연결시켜준다!
-> 오른쪽 자식이 있더라도 문제될 건 없고, 자식이 없으면 그냥 nullptr과 연결된거기 때문에 트리구조에 지장은 없다

7. childNode를 해제
8. 해제한뒤 return; 하기 때문에 함수가 종료된다
9. 함수가 후속자 처리를 완료한 뒤 return 하기 때문에 그 뒤의 로직인 delete currentNode는 수행하지 않는다
   

---

이진탐색트리 중위 순회 사용

• 앞에서 배웠던 중위순회를 사용하여 오름차순으로 정렬

// 중위순회
void Inorder(Node* root)
{
    if (root != nullptr)
    {
        Inorder(root->left);
        cout << root->data << " ";
        Inorder(root->right);
    }
}

---

Destroy( )함수 & Root ( ) 반환 함수

• Destroy함수는 root가 가리키는 노드가 있을때 재귀적으로 left와 right를 들어가고 해당 노드가 root가 되니 다 해제 해주기
• Root함수는 root값을 반환해주는 함수다

void Destroy(Node* root)
{
    if (root != nullptr)
    {
        Destroy(root->left);
        Destroy(root->right);

        delete root;
    }
}
Node* Root()
{
    return root;
}

---

Find( ) 함수 : 값 찾기

매개변수로 들어온 값이 내가 찾는 값이 맞는지 아닌지를 반환해주는 bool타입 함수

bool Find(T data)
{
    Node* currentNode = root;

    if (currentNode == nullptr)
    {
        return false;
    }
    else
    {
        while (currentNode != nullptr)
        {
            if (currentNode->data == data)
            {
                return true;
            }
            else
            {
                if (currentNode->data > data)
                {
                    currentNode = currentNode->left;
                }
                else
                {
                    currentNode = currentNode->right;
                }
            }
        }
        return false;
    }
}

1. 노드를 순회할 currentNode 포인터 생성 후 시작은 root를 가리킴

2. currentNode가 nullptr과 같다면 가리키는 노드가 없고 비어있는 상태 : false 반환

3. currentNode의 값이 내가찾는 값(매개변수 값)과 같다면 : true 반환

4. 내가 찾는 값이 currentNode값보다 작으면 currentNode를 왼쪽으로 이동

5. 내가 찾는 값이 currentNode값보다 크면 currentNode를 오른쪽으로 이동

6. currentNode를 다 순회했는데도 값을 못찾으면 false 반환

---

소멸자

~BinarySearchTree()
{
    Destroy(root);
}

---

메인 함수

int main()
{
    BinarySearchTree<int> binarySearchTree;

    binarySearchTree.Insert(15);
    binarySearchTree.Insert(20);
    binarySearchTree.Insert(10);
    binarySearchTree.Insert(13);
    binarySearchTree.Insert(11);
    binarySearchTree.Insert(12);
    binarySearchTree.Insert(9);

    binarySearchTree.Remove(10);

    binarySearchTree.Inorder(binarySearchTree.Root());

    cout << endl;

    cout << binarySearchTree.Find(12) << endl; // 찾았으니 true (1)



    return 0;
}

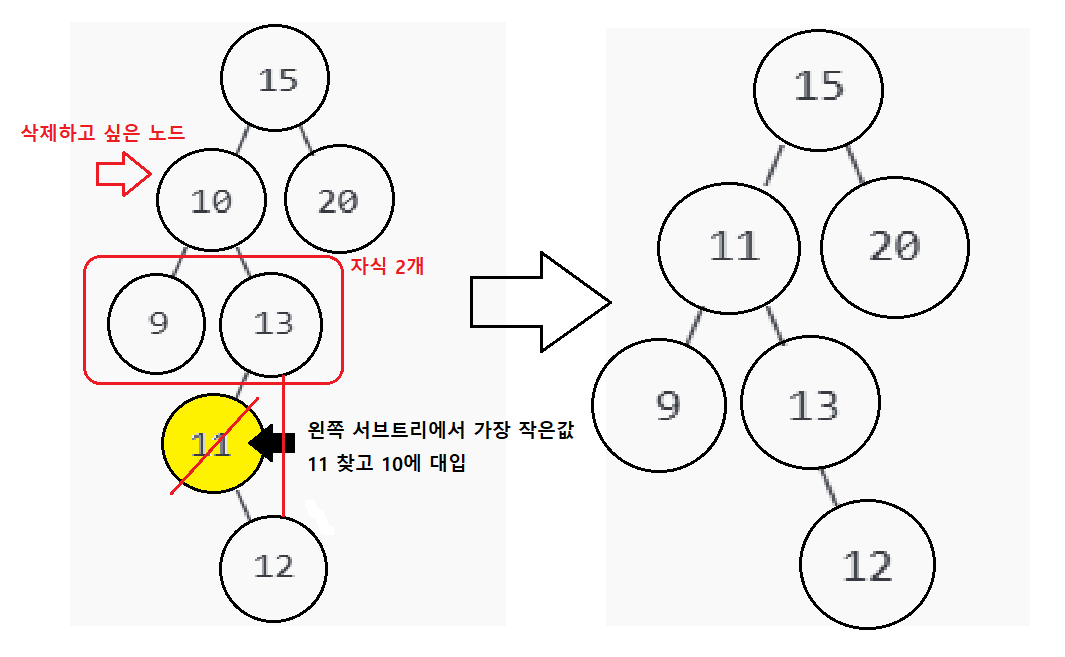
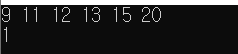
오름차순 정렬 결과 : 9 11 12 13 15 20 (10제거 후의 값임)
Find(12) 매개변수 12의 값을 찾았으니 return true

---

이진 탐색 트리의 장/단점

장점

• 시간복잡도가 O(logN)으로 탐색, 삽입, 삭제가 효율적이다

단점

• 트리가 한쪽으로 치우치면 시간복잡도가 O(n)으로 비효율적이라, 이럴 경우 균형 이진 탐색 트리로 구현해야한다