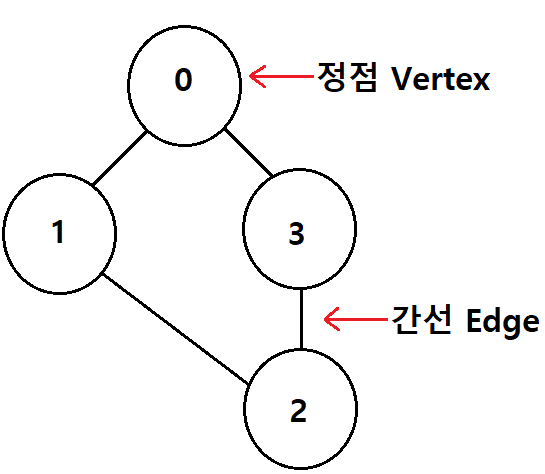
그래프
그래프를 구현하는 방법은 2가지가 있다
1. 그래프의 정점을 2차원 배열로 표현하는 인접행렬
2. 연결리스트로 표현하는 인접리스트
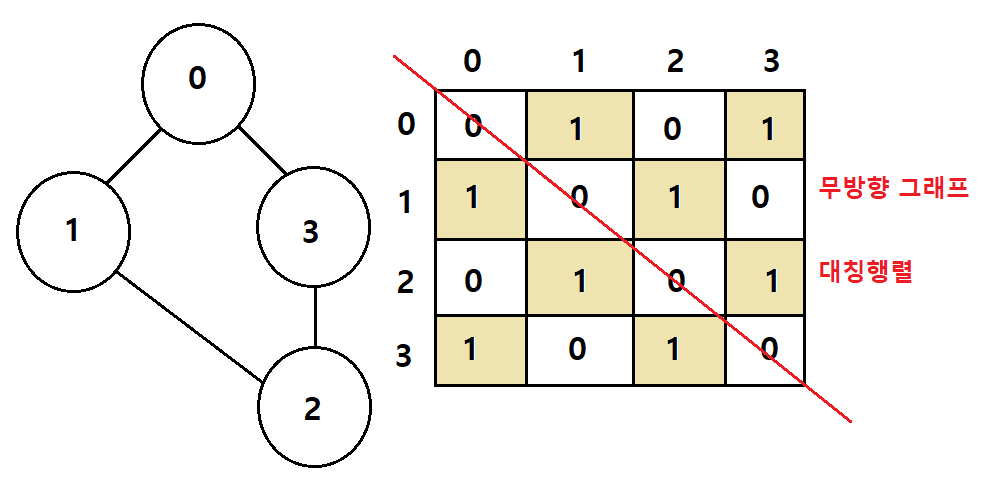
또한 그래프는 무방향 그래프와 방향그래프로도 나뉘는데
- 무방향 그래프: 양방향으로 이동이 가능하고 인접행렬 구조에서 대칭행렬을 이룬다
- 방향 그래프: 간선의 방향으로만 이동이 가능하고 인정행렬 구조에서 대칭행렬이 아니기도 한다
요소들이 정점과 간선으로 연결되어 관계를 표현하는 자료구조
- 정점: 노드라고 하며 그래프에 저장되는 기본 원소
- 간선: 정점과의 관계를 나타내는 선
- 차수: 정점에 연결된 간선의 수 / (ex) 0의 차수는 2
인접행렬로 구현
클래스 생성 & 생성자에서 초기화
-
template 형식으로 클래스를 구현하여 메인함수에서 자료형을 지정하게 하였다
-
정점(Vertex)의 갯수 : size 변수
-
정점을 생성하고 담아둘 배열
-
정점들을 연결하기 위해 사용되는 2차원배열(인접행렬)
-
2차원 배열의 크기는 넉넉하게 10 x 10
-> 보통은 2차원 배열의 크기는 정점 수 x 정점 수
#include <iostream>
#define SIZE 10
using namespace std;
// 그래프
// 인접행렬 그래프
template <typename T>
class AdjacencyMatrix
{
private:
// 정점의 개수
int size;
// 정점의 집합(배열)
T vertex[SIZE];
// 인접 행렬(2차원 배열) int
int matrix[SIZE][SIZE];
public:
AdjacencyMatrix()
{
size = 0;
for (int i = 0; i < SIZE; i++)
{
vertex[i] = NULL;
for (int j = 0; j < SIZE; j++)
{
matrix[i][j] = NULL;
}
}
}Insert( ) 함수 : 정점 생성
void Insert(T data)
{
// 정점을 생성
if (size >= SIZE)
{
cout << "Adjaceney Matrix OverFlow" << endl;
}
else
{
vertex[size++] = data;
}
}- size값이 내가 지정해둔 SIZE보다 크다면 2차원 배열의 크기를 넘어가기 때문에 오버플로우 발생
- 정점의 집합에 데이터를 넣고 size 증가
-> 데이터를 가진 정점이 생성되었다
Connect( ) 함수 : 정점 연결
void Connect(int i, int j)
{
if (size <= 0)
{
cout << "Adjancency Matrix is Empty" << endl;
}
else if (i >= SIZE || j >= SIZE)
{
cout << "Index Out of Range" << endl;
}
else
{
matrix[i][j] = 1;
matrix[j][i] = 1;
}
}- 매개변수로 들어온 i, j를 배열의 인덱스에 넣어서 연결시키고 간선 추가
Show( ) 함수 : 정점과 간선 상태를 보여주는 함수
void Show()
{
if (size <= 0)
{
cout << "Adjacency Matrix is Empty" << endl;
}
else
{
cout << " ";
for (int i = 0; i < size; i++)
{
cout << vertex[i] << " ";
}
cout << endl;
for (int i = 0; i < size; i++)
{
cout << vertex[i] << " ";
for (int j = 0; j < size; j++)
{
cout << matrix[i][j] << " ";
}
cout << endl;
}
}
}메인 함수
int main()
{
AdjacencyMatrix <char> adjacencyMatrix;
adjacencyMatrix.Insert('A');
adjacencyMatrix.Insert('B');
adjacencyMatrix.Insert('C');
adjacencyMatrix.Insert('D');
adjacencyMatrix.Connect(0, 1);
adjacencyMatrix.Connect(0, 2);
adjacencyMatrix.Connect(1, 3);
adjacencyMatrix.Show();
return 0;
}- char 타입의 객체를 생성
- 객체에 접근하여 정점을 4개 생성한다 (A B C D)
- Connect 함수를 통해 해당 인덱스 2개를 연결시켜준다
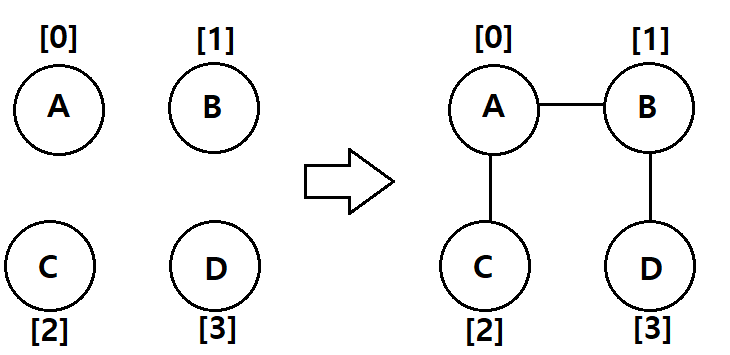
- Show( ) 함수로 정점과 정점끼리 연결된 간선을 확인해본다

대칭 행렬을 이루고 있다!
그래프 - 인접행렬의 장/단점
인접행렬의 장점
- 2차원 배열안의 모든 정점들의 간선 정보가 있기 때문에 두 정점을 연결하는 간선을 조회할때 시간복잡도가 O(1)
->배열안의 간선 수만 확인하면 된다
- 정점 차수를 구할때는 n번째 행의 값을 모두 더하면 되기 때문에 시간복잡도 O(n)
인접행렬의 단점
- 간선의 수와 무관하게 무조건 n² 크기의 2차원 배열이 필요하다
-> 간선이 몇개 없는데 정점의 수가 많을 경우, 2차원 배열의 크기가 커지고 남는 공간이 많아져 메모리가 낭비되어 비효율적이다
- 그래프 안의 모든 간선의 수를 알아내려면 인접행렬 전체를 확인해야 하기 때문에 시간복잡도 O(n²)
인접리스트로 구현
클래스 생성 & 초기화
-
teplate T로 클래스를 정의하였고 메인함수에서 자료형 타입 지정해주어야 한다
-
data 변수와 다음 노드를 가리킨 next 포인터
-
Node구조체 안에 Node 생성자를 만들기
Node ( data, Node * link = nullptr)
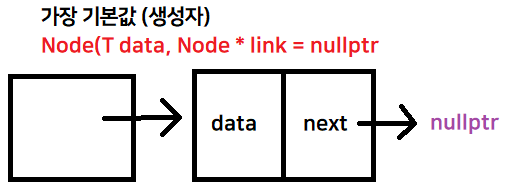
매개변수로 들어오는 data 값과, 다음 노드를 가리키는 포인터를 받는다
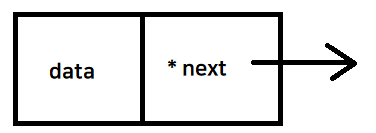
매개 변수로 들어온 link는 기본적으로 nullptr을 가리키게 설정
#include <iostream>
#define SIZE 10
using namespace std;
template <typename T>
class AdjacencyList
{
private:
struct Node
{
T data;
Node* next;
Node(T data, Node* link = nullptr)
{
this->data = data;
next = link;
}
};
int size; // 정점의 갯수
T vertex[SIZE]; // 정점의 집합
Node* list[SIZE]; // 인접 리스트
public:
AdjacencyList()
{
size = 0;
for (int i = 0; i < SIZE; i++)
{
vertex[i] = NULL;
list[i] = NULL;
}
}Insert( ) 함수 : 정점 생성
- 정점을 생성하고 vertex 배열안에 값 넣어주기
void Insert(T data)
{
if (size >= SIZE)
{
cout << "Adjacency List OverFlow" << endl;
}
else
{
vertex[size++] = data;
}
}Connect( ) 함수 : 정점 연결
-
매개변수로 u , v 값을 받는다
-
size가 0보다 작다는 것은 인접리스트가 비어있는 상태 (즉, 정점이 하나도 없는 것)
-
u 나 v 둘중 하나라도 size 값을 넘어가면 범위를 초과한 상태
-
값이 새로 들어와서 연결되는 느낌이 PushFront( )함수와 유사한 느낌이다
- 여기서 앞에 Node생성자의 매개변수를 받을 수 있다
매개변수로 받은 link는 next가 된다 (next = link)
이 말의 뜻은 next 포인터가 다음 노드를 가리킬 포인터가 된다는 것
ex)
- node1객체는 data가 10, 다음 노드를 가리키는 건 기본값 nullptr
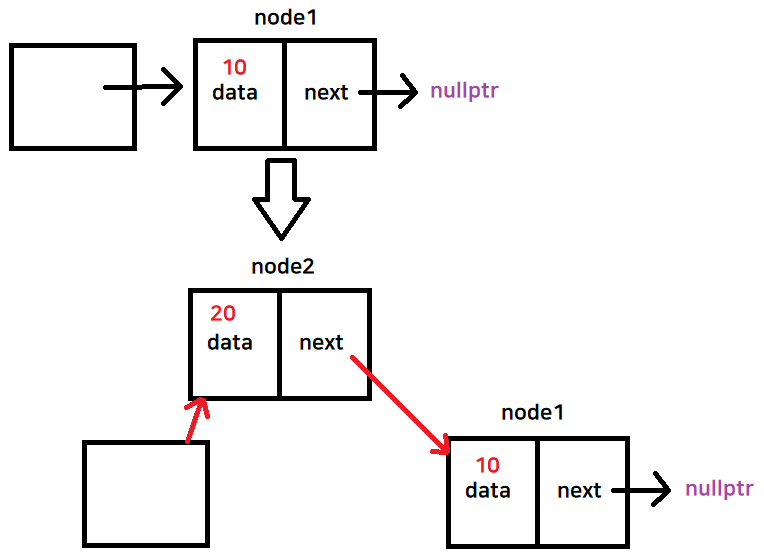
즉, node1 = data : 10 , * next : nullptr - node2객체는 data 가 20, 다음 노드를 가리키는 포인터가 node1
즉, link가 node1을 가리키는 포인터임. next = link가 되어서 node2의 next포인터가 node1을 가리킨다
Node node1 = new Node(10); Node node2 = new Node(20, node1);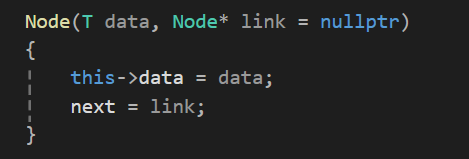
- 여기서 앞에 Node생성자의 매개변수를 받을 수 있다
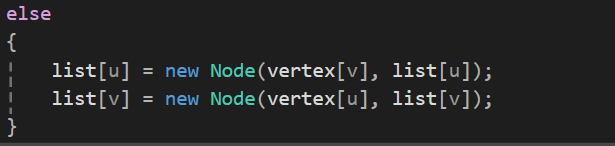
-> 내가 넣고 싶은 데이터의 값 : vertex[v] -> 정점배열안에 있는 정점
-> 내가 연결하고 싶은 값 : list[u] -> 기존의 list 포인터 배열이 가리키고 있던 곳
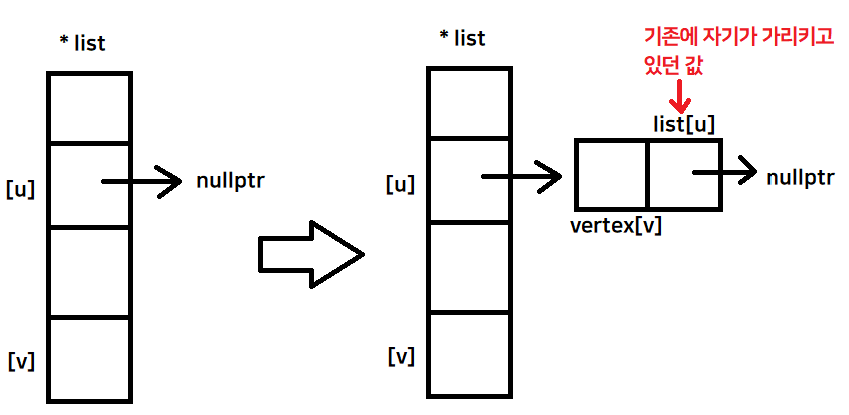
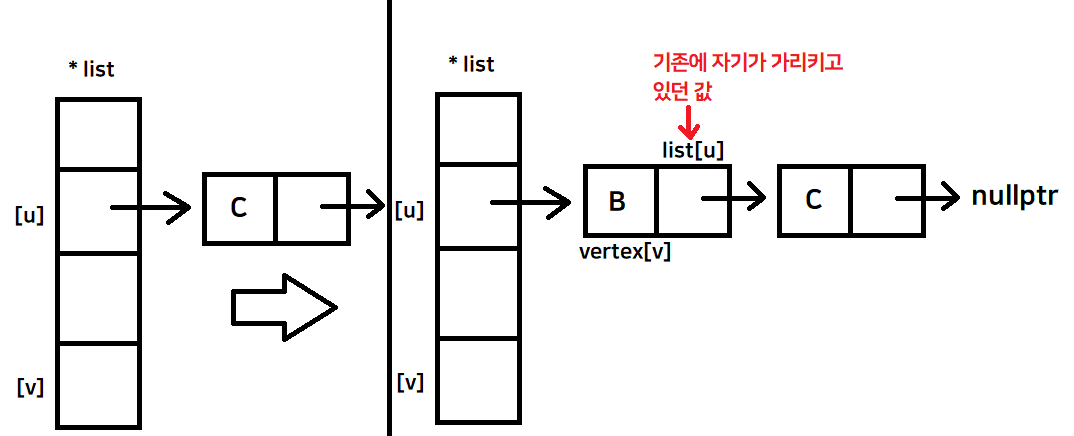
void Connect(int u, int v)
{
if (size <= 0)
{
cout << "Adjancency List is Empty" << endl;
}
else if (u >= size || v >= size)
{
cout << "index Out of Range" << endl;
}
else
{
list[u] = new Node(vertex[v], list[u]);
list[v] = new Node(vertex[u], list[v]);
}
}Show( ) 함수 : 정점과 간선 상태를 보여주는 함수
- 인접리스트는 연결리스트로 구현하기 때문에 리스트를 순회해줄 currentNode 포인터가 필요하다
- 각 정점마다 들어있는 연결리스트들을 다 순회
void Show()
{
for (int i = 0; i < size; i++)
{
cout << vertex[i] << " : ";
Node* currentNode;
currentNode = list[i];
while (currentNode != nullptr)
{
cout << currentNode->data << " ";
currentNode = currentNode->next;
}
cout << endl;
}
}소멸자
~AdjacencyList()
{
for (int i = 0; i < SIZE; i++)
{
if (list[i] != nullptr)
{
delete[] list[i];
}
}
}메인 함수
int main()
{
AdjacencyList<char> adjacencylist;
adjacencylist.Insert('A');
adjacencylist.Insert('B');
adjacencylist.Insert('C');
adjacencylist.Insert('D');
adjacencylist.Connect(0, 1);
adjacencylist.Connect(0, 2);
adjacencylist.Connect(1, 2);
adjacencylist.Connect(2, 3);
adjacencylist.Show();
return 0;
}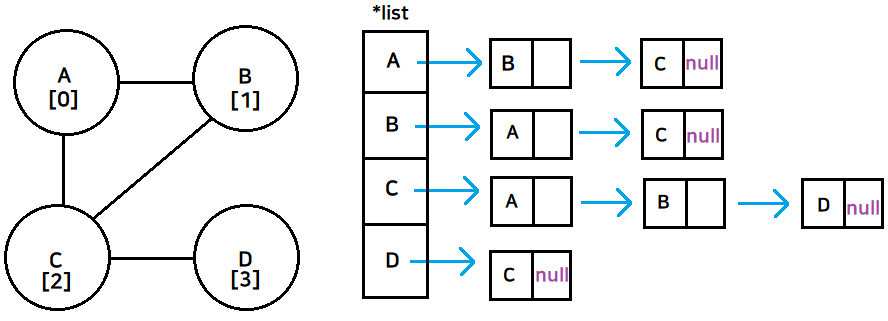
인접리스트 특징
-
간선의 수가 적은 최소 그래프에서 효과적이다
-
무방향 그래프에선 노드의 수 만큼 연결리스트가 만들어진다
-
연결리스트의 화살표는 간선의 수
-
인접행렬과 다르게 공간복잡도가 O(V + E)
-
간선 탐색 시간 : 인접리스트를 순차적으로 탐색해야 하기 때문에 간선 수에 비례해서 시간이 소요 -> O(E)
V = 정점 수, E = 간선 수
-
간선 추가/삭제 = O(1)
인접리스트 장점
- 존재하는 간선만 관리하면 되기 때문에 메모리 사용이 효율적이다
- 하지만, 모든 간선의 수는 head부터 인접리스트를 모두 탐색해야 하기 때문에 시간복잡도가 O(N + E) (간선 수(E) 만큼)