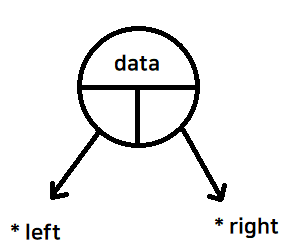
이진 트리
각 노드가 최대 2개의까지의 자식노드를 가진 트리
트리지만, 1차원 배열로 표현할 수 있다는 특징이 있다
노드의 구조체
#include <iostream>
#define SIZE
// 이진 트리
using namespace std;
struct Node
{
int data;
Node* left;
Node* right;
};
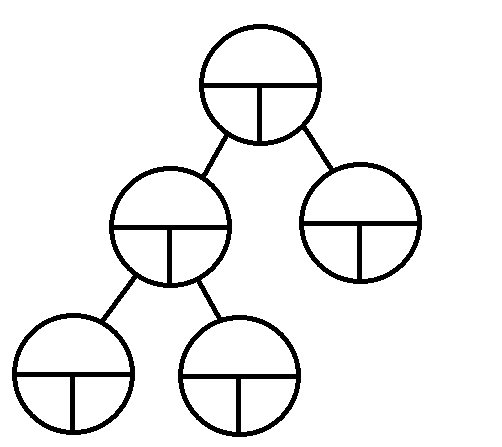
- 위 그림이 이진트리의 모습이다
- 이진트리도 모양이 다양하고 종류도 많지만, 나중에 알아보고 지금은 이진트리의 구조와 노드 순회에 대해 알아볼 것 이다
CreateNode( ) 함수
- newNode를 생성해주고 메인함수에서 매개변수로 data 값과 왼쪽, 오른쪽에 들어갈 노드를 받아온다
// 노드 생성
Node* CreateNode(int data, Node* left, Node* right)
{
Node* newNode = new Node();
newNode->data = data;
newNode->left = left;
newNode->right = right;
return newNode;
}순회
- root를 기준으로 순회방식을 다르게 할 수 있는데 이렇게 하면 결과값도 다 다르게 나온다 !!
- 순회 하는 방식은 재귀함수를 사용하는 것이 편하다!
-> 재귀함수 특성상 해당 함수가 여러차례 실행되고 그 함수가 끝나면 이전 자기 자신에서 자신을 호출한 곳으로 다시 되돌아가서 코드가 남아있다면 나머지 로직을 수행하게 되고 함수가 종료된다
매개변수로 들어온 게 Node * root기 때문에 내가 있는 곳이 곧 root
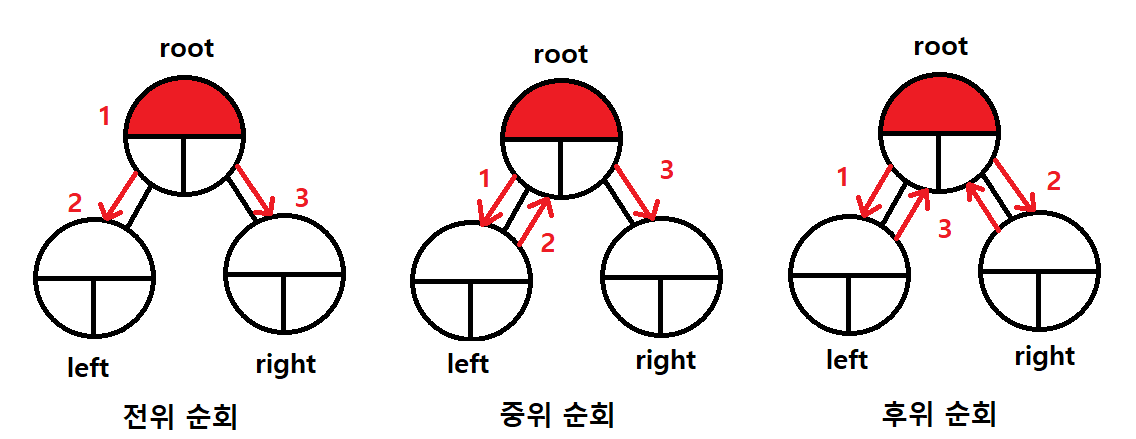
전위 순회 (PreOrder)
- root -> left -> right
- 내가 있는 위치인 root의 데이터를 먼저 출력한 뒤 left로 이동
- 말단 자식의 left와 right가 모두 nullptr을 가리키면 이전 노드로 돌아가서 재귀함수 로직 마저 수행
- 현재 사진에서 4까지 도착하였지만 그 아래 자식들은 다 nullptr이기 때문에 다시 2로 돌아간다
- 2에서는 root 데이터를 출력했고, 왼쪽도 들어갔기 때문에 남은 로직인 오른쪽으로 이동을 수행한다

// 전위 순회
void PreOrder(Node* root)
{
if (root != nullptr)
{
// 데이터를 먼저 출력하고 이동
cout << root->data << " ";
PreOrder(root->left);
PreOrder(root->right);
}
}출력값: 1 2 4 5 3 6 7
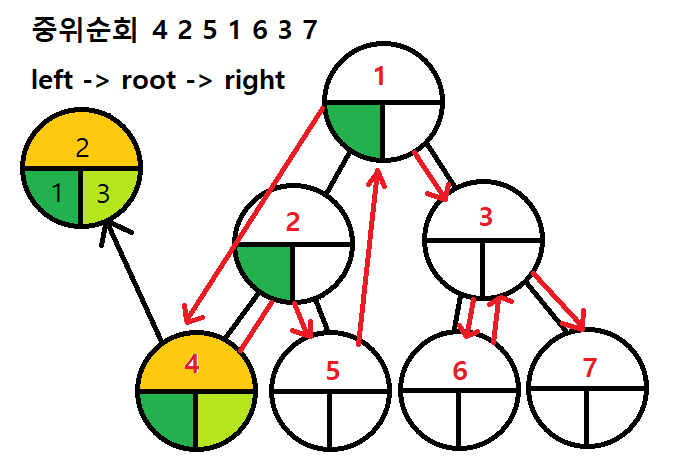
중위 순회 (InOrder)
- left -> root -> right
- 중위순회는 left를 다 살펴보고 left가 nullptr일 경우 root의 데이터를 출력한 뒤 right까지 다 보는 것이 함수의 루틴이다
- 함수의 로직을 다 끝내면 다시 위의 노드로 돌아가서 나머지 루틴을 실행한다
- 여기서는 left로 계속 들어간 뒤 4에 도달하고 root의 데이터를 출력한 뒤 right를 확인한다
- 4에서 함수가 모두 종료되어 다시 2로 돌아가면, 2는 left쪽 로직을 끝냈고 2데이터를 출력한 후 right인 5로 들어간다
중위순회를 사용하면 오름차순 정렬을 할 수 있다!
- 왼쪽 노드부터 root를 거쳐 오른쪽 노드로 이동한다
- 이진 탐색 트리(Binary Search Tree)에서는 노드의 값이 무조건 left < root < right 순서이다
- 중위순회 방식을 통해 오름차순으로 나오게 된다
// 중위 순회
void InOrder(Node* root)
{
if (root != nullptr)
{
InOrder(root->left);
cout << root->data << " ";
InOrder(root->right);
}
}출력값: 4 2 5 1 6 3 7
후위 순회 (PostOrder)
- left -> right -> root
- 노드의 left와 right를 확인을 다 하고 root의 데이터를 출력한다
- 사진에서 left로 먼저 들어간 뒤 다음 노드도 left가 있으니 들어간다
- 다음 left가 nullptr이면 left함수 중지하고 right로 들어간 뒤 확인하고 다음 데이터 출력
- 아래의 사진에서 4까지 들어간 후 left가 nullptr이라 right를 확인한다
- right도 nullptr이기 때문에 root인 4 데이터를 출력하고 다시 위의 노드로 이동
- 위의 노드인 2에선 아직 left 로직만 확인하였으니 다른 로직을 다 수행해야함

// 후위 순회
void PostOrder(Node* root)
{
// root 가 nullptr이 아니면 왼쪽부터 감
// root가 nullptr이면 함수 종료 & 전으로 돌아가서 오른쪽 탐색
if (root != nullptr)
{
PostOrder(root->left);
PostOrder(root->right);
// 다 이동한 뒤 데이터 출력
cout << root->data << " ";
}
}메인함수
int main()
{
Node* node7 = CreateNode(7, nullptr, nullptr);
Node* node6 = CreateNode(6, nullptr, nullptr);
Node* node5 = CreateNode(5, nullptr, nullptr);
Node* node4 = CreateNode(4, nullptr, nullptr);
Node* node3 = CreateNode(3, node6, node7);
Node* node2 = CreateNode(2, node4, node5);
Node* node1 = CreateNode(1, node2, node3);
PostOrder(node1);
cout << endl;
PreOrder(node1);
cout << endl;
InOrder(node1);
return 0;
}
