
1️⃣ 제로 - 10773
문제

정답
import java.io.*;
import java.util.*;
public class Main {
static List<Integer> arr = new ArrayList<>();
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
Stack<Integer> stack = new Stack<>();
int n = Integer.parseInt(br.readLine());
for (int i = 0; i < n; i++) {
int num = Integer.parseInt(br.readLine());
if (num == 0) {
stack.pop();
} else {
stack.push(num);
}
}
int ans = 0;
while (!stack.isEmpty()){
ans += stack.pop();
}
bw.write(ans + "\n");
bw.flush();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
문제에서 “가장 최근에 쓴 수를 지우고”라는 문장을 토대로 스택을 사용해야 하는 문제임을 알 수 있다.
이를 통해서 Last In First Out인 스택을 사용하는 문제임을 유추 할 수 있다.
스택을 사용하면 어려운 문제가 아니기에 쉽게 풀 수 있을 것이라 생각한다.
2️⃣ 감소하는 수 - 1038
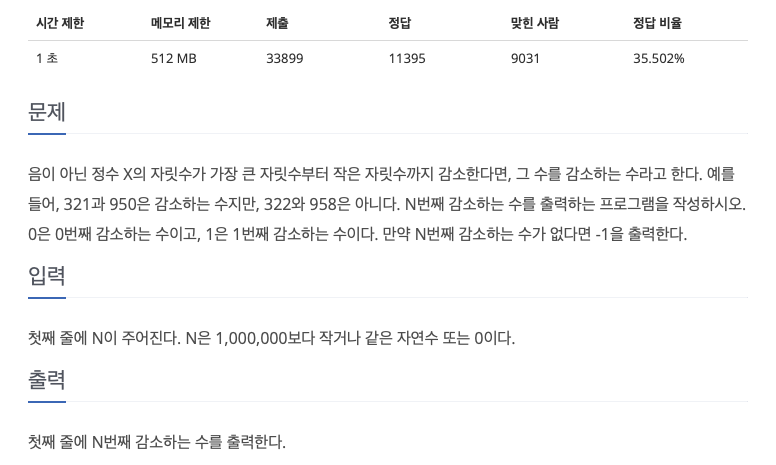
문제
정답
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class Main {
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
Queue<Long> queue = new LinkedList<>();
List<Long> decNums = new ArrayList<>();
for (int i = 0; i <= 9; i++) {
queue.add((long) i);
decNums.add((long) i);
}
while (!queue.isEmpty()) { // BFS 탐색을 수행하여 감소하는 수를 생성
long num = queue.poll(); // 현재 숫자 꺼내기
long lastDigit = num % 10; // 마지막 자리 숫자
for (int j = 0; j < lastDigit; j++) { // 마지막 자리 숫자를 뒤에 붙여서 새로운 감소하는 수 생성
long newNum = num * 10 + j;
queue.add(newNum);
decNums.add(newNum);
}
}
if (n >= decNums.size()) {
bw.write(-1 + "\n");
} else {
bw.write(decNums.get(n) + "\n");
}
bw.flush();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
문제는 BFS(완전 탐색)을 이용하여 풀 수 있다.
문제에서 Queue<Long>를 사용하여 감소하는 수를 생성한다.
이 때 한 자리 숫자(0~9)는 모두 감소하는 수이므로, 큐에 미리 삽입한다.
그리고 BFS를 이용한 감소하는 수를 생성한다.
while 문 안에서 큐에서 숫자를 하나씩 꺼내 마지막 자리 숫자보다 작은 숫자를 추가하여 새로운 감소하는 수를 만든다.
- 예를 들어,
4를 꺼내면 →40, 41, 42, 43등을 만들 수 있음.
이렇게 생성된 숫자는 큐에 삽입하여 탐색을 이어간다.
그리고 이 때 감소하는 수를 List<Long>에 저장하면서 차례대로 생성하므로, N번째 감소하는 수가 존재하면 출력하고, 없으면 1을 출력하면 된다.
3️⃣ 쉽게 푸는 문제 - 1292
문제

정답
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public void solution() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int idx = 1; // 구간 인덱스
int ans = 0;
for (int i = 1; i <= B; i++) {
for (int j = 0; j < i; j++) {
if (idx >= A && idx <= B) {
ans += i;
}
idx += 1;
}
}
bw.write(ans + "\n");
bw.flush();
bw.close();
}
public static void main(String[] args) throws IOException {
new Main().solution();
}
}
위 문제는 문제에서 주는 설명만 따라가면 되는 문제였다.
12233344445555 …
3 ~ 7 구간이면, 위 수열에서 아래와 같다.
12233344445555 …
나는 1부터 시작해서 구간의 종료인 B 구간까지 이중 반복문을 돌리는 방법을 택했다.
현재 반복문이 A와 B 구간 이내에 있는지를 판단할 수 있게 idx 변수를 사용함으로서 해당 구간의 합을 쉽게 구할 수 있었다.
배운 점
- 주어진 입력값의 범위 중 경계값을 기준을 삼으면 효과적인 반례가 된다.
