서론
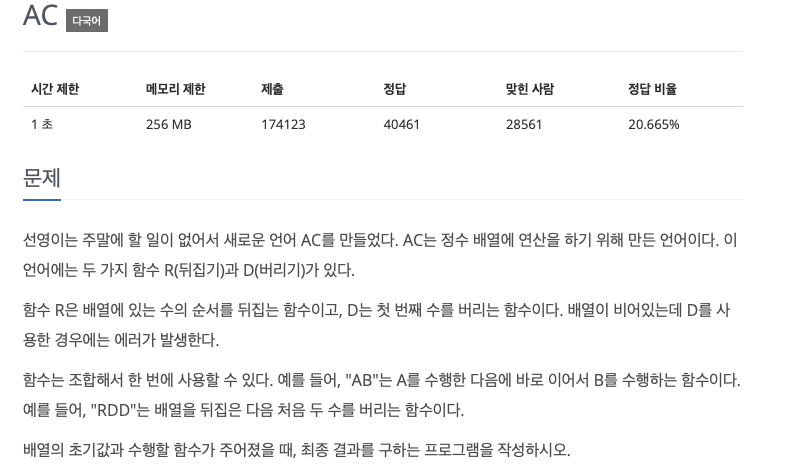

이번에 백준 5430번 알고리즘 문제를 풀다가 시간 복잡도로 인해 틀렸다.
매번 알고리즘 문제를 풀 때 저 1초라는 시간과 주어지는 입력값의 개수를 통해 어떤 근거로 어떤 시간 복잡도를 가진 알고리즘을 도출 해야 하는지가 궁금했다.
단순히 1초이면, ArrayList를 사용 하면 안되는건가? 아니면 입력값이 많으면 사용하면 안되는걸까?
이번 기회에 시간 복잡도에 대해서 더욱 공부하는 시간을 갖고자 한다.
시간 복잡도
알고리즘의 효율성은 알고리즘의 수행 시간 또는 알고리즘이 수행하는 동안 사용 되는 메모리 공간의 크기로 나타낼 수 있다.
이는 각각 시간 복잡도와 공간 복잡도라고 한다.
요즈음날에는 메모리의 성능이 향상 되었기에 일반적으로 알고리즘들을 비교 할 때는 시간 복잡도가 주로 사용 된다고 한다.
시간 복잡도는 알고리즘이 수행하는 기본적인 연산 횟수를 입력 크기에 대한 함수로 표현한다.
알고리즘의 복잡도를 표현 하는데는 아래와 같은 분석 방법들이 있다.
- 최악 경우 분석
- 평균 경우 분석
- 최선 경우 분석
이 중 최악 경우 분석으로 알고리즘의 복잡도를 나타내는데, 최악 경우 분석은 ‘어떤 입력이 주어지더라도 얼마 이상을 넘지 않는다’라는 표현이다.
최악의 경우 시간 복잡도를 표현하는 방법은 빅오 표기법이다.
빅오 표기법은 상한선을 활용하는 점근적 표기법을 의미한다.
예를 들어 어떤 프로그램의 연산 횟수가 f(x)일 때 함수의 최고차항을 남기고 차수를 지워 O(…)와 같이 표기 하면 된다.
즉, f(x) = 2x3+ 3x2 + 5라면 시간 복잡도를 O(x3)과 같이 표현하면 된다.
이렇게 최고차항만 남길 수 있는 이유는 x가 무한히 커질 수 있다는 가정 때문이다.
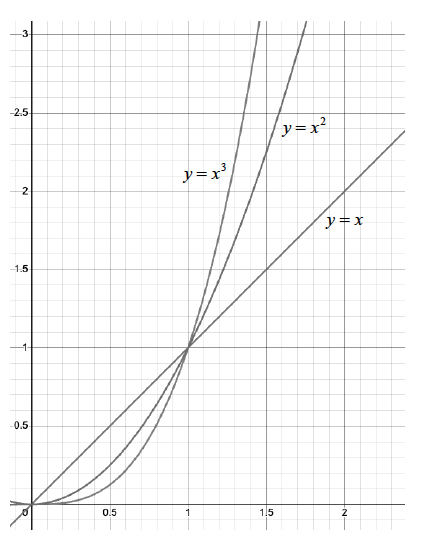
무한히 커진다고 하면, 최고 차항을 제외 한 나머지는 무시할 수 있을 정도로 작아지기 때문이다.
왜 효율적인 시간 복잡도를 가져야 할까?
코테 맞기 위해서요.
같은 대답은 나중에 하자.
극단적인 예를 들면 들 수록 이 SW의 세계에서 이유는 명확해진다.
예를 들어 10억개의 숫자를 정렬하는데 일반적인 PC에서 O(n2) 알고리즘은 300여년이 걸린다.
그러나 O(nlogn) 알고리즘은 5분만에 정렬 할 수 있다.
이렇듯 값 비싼 하드웨어를 스펙업 시키는 것 보다 효율적인 알고리즘 개발이 훨씬 더 경제적이라고 할 수 있다.
그렇다면 코테에서의 시간 복잡도는?
*매번 알고리즘 문제를 풀 때 저 1초라는 시간과 주어지는 입력값의 개수를 통해 어떤 근거로 어떤 시간 복잡도를 가진 알고리즘을 도출 해야 하는지가 궁금했다.
단순히 1초이면, ArrayList를 사용 하면 안되는건가? 아니면 입력값이 많으면 사용하면 안되는걸까?*
위 문장은 내가 서론에서도 이야기 했던 이 글을 쓰게 된 핵심적인 질문이다.
일반적으로 아래와 같은 경험적 기준을 세우고 문제를 풀면 도움이 된다고 한다.
제한 시간이 1초인 문제는 연산 횟수가 3,000만이 넘는 알고리즘을 사용 하면 안된다.
이 때 제한 시간이 1초인 문제에 각 시간 복잡도 별로 허용할 수 있는 최대 연산은 다음과 같다고 한다.
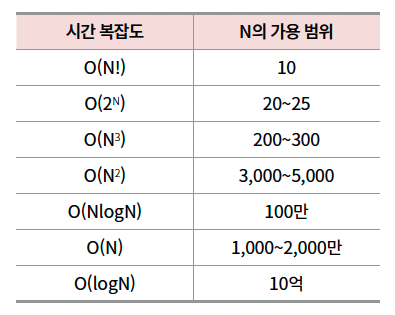
출처 : https://wikidocs.net/232020
이제 예시 코드를 보면서 위 경험적 기준을 적용 시켜보자.
예시 코드
public void R(List<Integer> arr) {
Collections.reverse(arr);
}
public boolean D(List<Integer> arr) {
if (arr.isEmpty()) {
return false;
} else {
arr.remove(0);
return true;
}
}위 문제에서는 N 즉, arr의 길이가 최대 10만이라고 했다.
이 때 D 메서드, 즉 ArrayList의 remove에는 O(N)의 시간 복잡도를 가지게 된다.
이 때 p, 즉 메서드 호출 명령어의 최대 길이는 10만이다.
최악의 경우를 따져 보았을 때 10만 x 10만 = 100억 번의 연산이 필요해진다.
이러면 최대 3,000만번을 훨씬 넘어가므로 ArrayList를 사용한 알고리즘은 사용 불가 하게 된다.
이를 통해 우리는 문제에 주어진 시간 제한과 입력값 개수를 통해 어떤 시간 복잡도를 가진 알고리즘을 사용해야 할지를 감 잡을 수 있다.
여담으로 ArrayList의 정렬간에 사용 되는 대표적인 두 방법의 시간 복잡도를 이야기 하고, 글을 마무리 하겠다.
Arrays.sort(), O(n2)Collections.sort(), O(nlog(n))

