핵심 키워드 및 내용
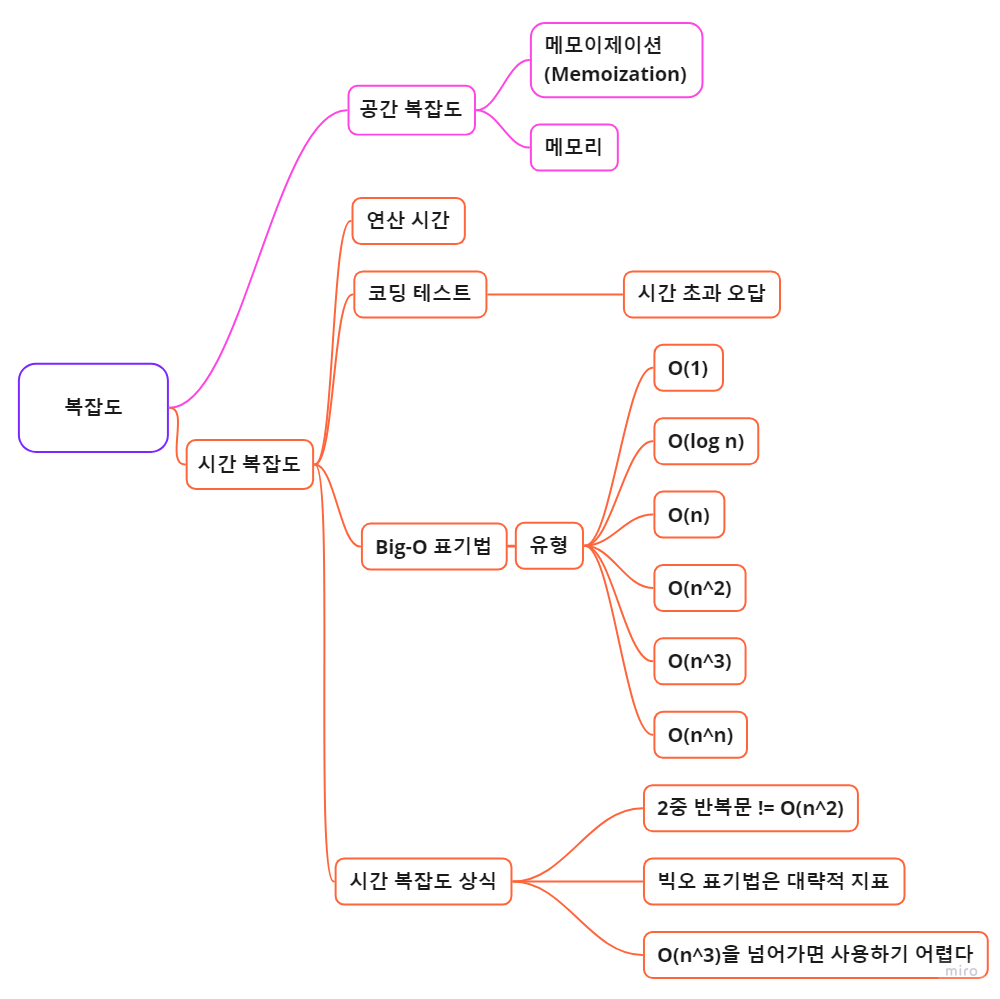
이 글에서 핵심이 되는 키워드와 내용을 마인드맵으로 작성해봤습니다.
ChatGPT 요약
복잡도는 알고리즘의 성능을 나타내는데, 시간 복잡도는 알고리즘의 실행 시간을, 공간 복잡도는 메모리 사용을 나타낸다. Big-O 표기법으로 시간 복잡도를 나타내며, 가장 빠르게 증가하는 항만을 고려한다.
복잡도란?
복잡도(Complexity)는 알고리즘의 성능을 나타내는 척도입니다.
- 시간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘이 얼마나 오래 걸리는지
- 공간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지
둘 중 어느 하나가 중요하다고 할 수 없고,
각각의 상황에 맞춰서 고려해야 할 성능 지표입니다.
메모리를 좀 더 사용하더라도 시간적으로 이점을 얻는 기법도 있습니다.
이것을 메모이제이션(Memoization) 기법 이라고 합니다.
시간 복잡도

백준, 프로그래머스에서 문제를 풀면서 시간 제한 때문에 오답으로 처리되는 경우가 많습니다.
시간 제한은 작성한 프로그램이 모든 입력을 받아 처리하고,
실행 결과를 출력하는 데까지 걸리는 시간을 의미합니다.

시간 복잡도를 알아야 하는 이유
위와 같이 시간 제한 오답을 해결하기 위해 단순히 문제를 많이 풀어서는 해결되지 않습니다.
시간 복잡도에 대한 개념을 알고 내가 작성한 코드의 시간 복잡도를 대략적으로 알아야 합니다.
그리고 문제에서 입력 값의 범위를 보고 어느정도 연산 횟수를 고려해서 코드를 작성하면,
시간 초과로 인해 코딩 테스트 시간을 낭비하는 것을 줄일 수 있습니다.
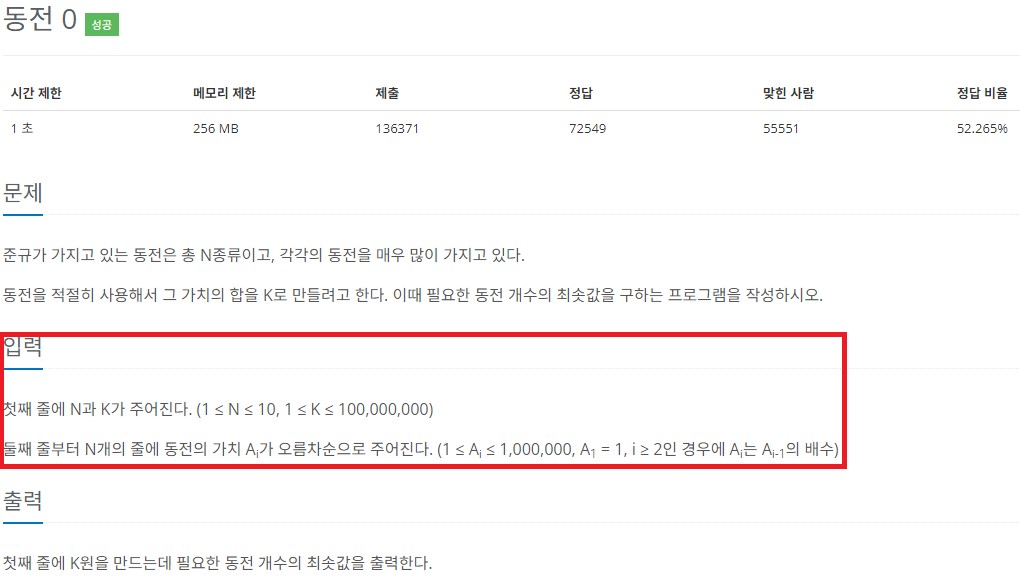
위 사진은 알고리즘 사이트인 백준의 문제(11047번 문제)입니다.
입력의 부분을 보면 N의 범위가 1 ~ 10 까지인 것을 볼 수 있습니다.
이것을 통해 이 문제는 O(N^3)의 시간 복잡도가 나오는 코드를 작성해도 통과할 가능성이 있습니다.
(위 문제는 그리디 알고리즘 문제입니다.)
시간 복잡도에 대한 개념과 알아야 하는 이유를 알아봤습니다.
이번에는 시간 복잡도를 표현할 때 사용하는 Big-O(빅오) 표기법에 대해 알아보겠습니다.
Big-O 표기법이란?
가장 빠르게 증가하는 항(상항)만을 고려하는 표기법
시간 복잡도는 입력에 대한 성능 지표를 뽑아냅니다.
그렇기 때문에 가장 성능에 영향을 많이 주는 함수의 상항만을 Big-O로 표기합니다.
예를 들어 5개의 정수가 들어있는 배열의 값을 전부 합하는 코드가 있습니다.
# N개의 정수가 담겨있는 array 배열
array = [1, 2, 3, 4, 5]
# 합계를 저장할 변수
sumNum = 0
# array 배열을 전부 더하는 반복문
for arrayNum in array:
sumNum += arrayNum
# array의 0 번째 인덱스를 sumNum에 더하는 연산
sumNum += array[0]
# 합계를 콘솔창에 출력
print(sumNum)위 코드의 시간 복잡도는 O(N)이 됩니다.
그 이유는 가장 영향력이 큰 부분은 N에 비례하는 연산을 수행하는 반복문이기 때문입니다.
sumNum += array[0]
반복문 연산 후에 0번째 인덱스를 더하는 연산은 영향력이 반복문에 적기 때문에 제외합니다.
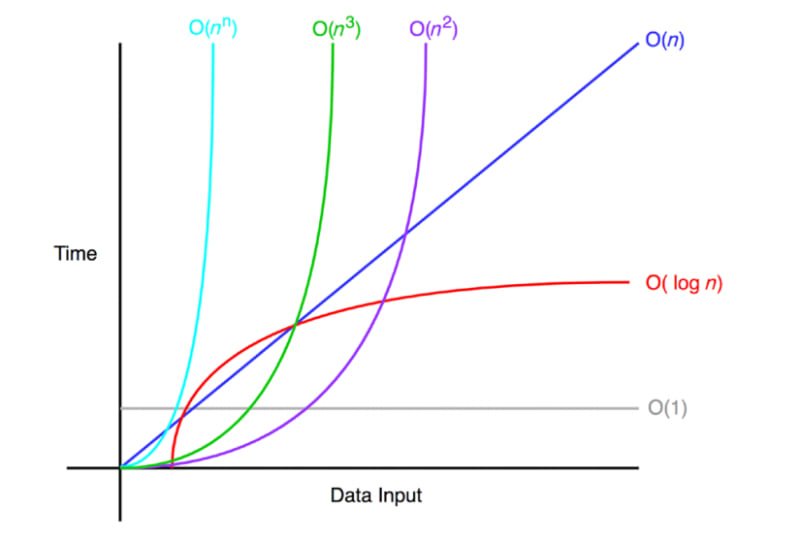
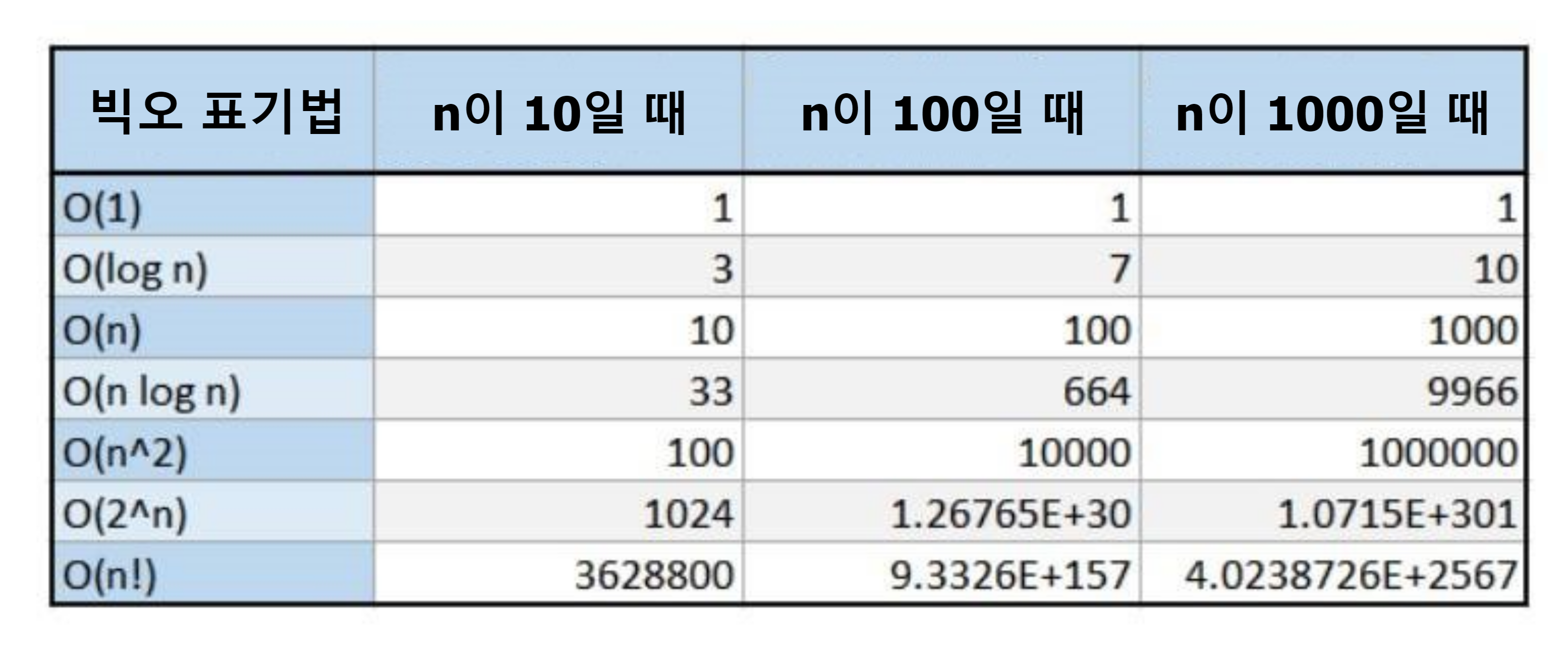
위 그래프는 Big-O 표기법을 시간과 입력 데이터을 기준으로 그래프로 나타낸 것입니다.
O(N^2) 이상은 데이터가 많아질 수록 시간이 기하급수적으로 늘어납니다.
무조건 O(N^n)은 안좋은 코드라고 단정 지을 수는 없지만 코딩 테스트를 기준으로 봤을 때,
통과를 하기 힘들 확률이 높습니다.
시간 복잡도 잘못된 상식
이번에는 시간 복잡도를 공부하면서 잘못된 내용들을 정리해봤습니다.
시간 복잡도를 잘못 이해하고 받아들여 생기는 문제에 대한 내용입니다.
- 2중 반복문의 시간 복잡도는 무조건 O(n²)이 아니다.
- 빅오 표기법이 항상 절대적인 것은 아니다.
2중 반복문 시간 복잡도 != O(n²)
대부분 코드를 보면 연산 횟수가 많이 실행되는 부분은 반복문이 작성된 부분입니다.
그래서 반복문을 제일 먼저 보고 해당 코드의 시간 복잡도를 측정하는 경우가 있습니다.
이것은 반은 맞고 반은 틀립니다.
array = [1, 2, 3, 4, 5]
sumNum = 0
for arrayNum in array:
for arrayNum2 in array:
sumNum += arrayNum2
print(sumNum)위 파이썬 코드의 시간 복잡도는 O(N^2)입니다.
코드에서 사용된 중첩된 두 개의 for 루프로 인해 전체 연산 횟수는 N * N이 되기 때문입니다.
만약에 반복문에서 다른 함수를 호출하면 내부 함수의 시간 복잡도 까지 고려해야 합니다.
빅오 표기법이 항상 절대적인 것은 아니다.
연산 횟수에서 N의 값이 작고 상수의 값이 더 크면 상수의 영향이 더 큽니다.
3N^3 + 5N^2 + 1,000,000
위와 같은 연산 횟수에서 N의 값이 10이라면
3N^3 + 5N^2 + 1,000,000 = 1,003,500가 됩니다.
상수의 연산 횟수가 훨씬 높아서 시간 복잡도에 영향을 줍니다.
O(N^3)을 넘어가면 사용하기 어렵다.
CPU 기반의 컴퓨터에서는 연산 횟수가 10억을 넘어가면 C언어 기준으로 통상 1초 이상의 시간이 소요된다.
코드의 시간 복잡도 추론해보기
문제 1
def find_duplicate(numbers):
seen = set()
for num in numbers:
if num in seen:
return num
seen.add(num)
return None
# 예제 사용법
numbers_list = [1, 2, 3, 4, 5, 2]
result = find_duplicate(numbers_list)
print(f"Duplicate number: {result}")
❗힌트와 정답을 보기 위해서는 아래 빨간색 박스를 드래그 해주세요.
힌트 보기
find_duplicate 함수에서는 주어진 리스트의 모든 요소를 한 번씩 순회하면서 중복된 숫자를 찾는 알고리즘입니다.
정답 보기
시간 복잡도 : O(N)
문제 2
def binary_search(arr, target):
low, high = 0, len(arr) - 1
while low <= high:
mid = (low + high) // 2
mid_value = arr[mid]
if mid_value == target:
return mid
elif mid_value < target:
low = mid + 1
else:
high = mid - 1
return -1
# 예제 사용법
sorted_list = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
target_element = 7
index = binary_search(sorted_list, target_element)
print(f"Index of {target_element}: {index}")❗힌트와 정답을 보기 위해서는 아래 빨간색 박스를 드래그 해주세요.
힌트 보기
이진 탐색은 정렬된 리스트에서 중간 값과 비교하여 범위를 반으로 줄여가며 탐색하는 알고리즘입니다.
정답 보기
시간 복잡도 : O(log n)
