[자료 구조] 동적 배열 구현 연습

구현할 부분

추가, 인덱싱, 삭제

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace Algorithm
{
    class Board
    {
        // c++과 c#에서 차이가 있음 Vector - List | List - LinkedList
        public int[] _data = new int[25]; //배열
        public List<int> _data2 = new List<int>(); // 동적 배열
        public LinkedList<int> _data3 = new LinkedList<int>();

        public void Initialize()
        {
            _data2.Add(101);
            _data2.Add(102);
            _data2.Add(103);
            _data2.Add(104);
            _data2.Add(105);

            int temp = _data2[2];

            //삭제
            _data2.RemoveAt(2);
        }

    }
}

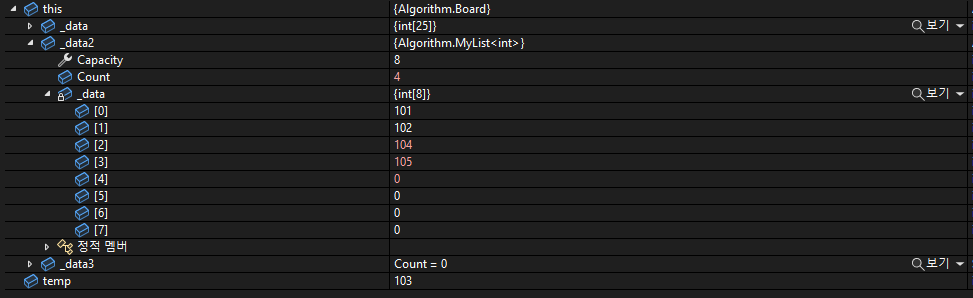
구현

    class MyList<T>
    {
        const int DEFAULT_SIZE = 1;
        T[] _data = new T[DEFAULT_SIZE];

        public int Count = 0; // 실제로 사용중인 데이터 개수
        public int Capacity { get { return _data.Length; } } // 예약된 데이터 개수 (여유분)

        public void Add(T item)
        {
            //1. 공간이 충분히 남아 있는지 확인한다
            if (Count >= Capacity)
            {
                //공간을 다시 늘려서 확보한다.
                T[] newArray = new T[Count * 2];
                for (int i = 0; i < Count; i++)
                    newArray[i] = _data[i];
                _data = newArray;
            }

            //2. 공간에다가 데이터를 넣어준다
            _data[Count] = item;
            Count++;
        }

        public T this[int index]
        {
            get { return _data[index]; }
            set { _data[index] = value; }
        }

        public void RemoveAt(int index)
        {
            //삭제할 값의 뒷부분 부터 한 칸씩 앞으로 땡김
            for (int i = index; i < Count - 1; i++)
                _data[i] = _data[i + 1];
            //땡긴 후 마지막 인덱스의 값을 초기화
            _data[Count - 1] = default(T);
            Count--;
        }
    }   

시간 복잡도 계산

Add(T item)

데이터 개수가 n개이면 연산을 n번해야 하니 시간 복잡도를 O(N)이라고 생각할 수 있다.
하지만 Count >= Capacity 일 경우 데이터가 두 배씩 계속 늘어나기 때문에 시간 복잡도를 계산할 때 이 부분을 무시한다.
점점 데이터가 많아질 수록 재할당하는 횟수가 줄어들기 때문이다.
즉 특이 케이스로, 동적 배열에서 아이템을 추가하는 것은 상수 시간 복잡도라고 흔히들 한다

O(1) : 이사 비용은 무시한다.

public void Add(T item)
        {
            //1. 공간이 충분히 남아 있는지 확인한다
            if (Count >= Capacity)
            {
                //공간을 다시 늘려서 확보한다.
                T[] newArray = new T[Count * 2];
                for (int i = 0; i < Count; i++)
                    newArray[i] = _data[i];
                _data = newArray;
            }

            //2. 공간에다가 데이터를 넣어준다
            _data[Count] = item;
            Count++;
        }

T this[int index]

O(1) : 연산이 1개이기 때문에

public T this[int index]
        {
            get { return _data[index]; }
            set { _data[index] = value; }
        }

RemoveAt(int index)

데이터에 비례한 for문
for (int i = index; i < Count - 1; i++) 이 존재한다.
즉 big-O 표기법에서의 N과 같은 Count가 있다.

O(N) : 최악의 경우

public void RemoveAt(int index)
        {
            //삭제할 값의 뒷부분 부터 한 칸씩 앞으로 땡김
            for (int i = index; i < Count - 1; i++)
                _data[i] = _data[i + 1];
            //땡긴 후 마지막 인덱스의 값을 초기화
            _data[Count - 1] = default(T);
            Count--;
        }