MNIST - MLP
1. 데이터 불러오기 / 전처리
- MNIST 데이터는 픽셀 값이 0~255 범위의 정수
import tensorflow as tf
mnist = tf.keras.datasets.mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 딥러닝 모델 학습에 적합하도록 데이터를 0~1 범위로 정규화
# 정규화 이후 : float32 타입의 NumPy 배열. 각 이미지의 픽셀 값은 [0,1] 범위.
X_train, X_test = X_train / 255.0, X_test / 255.02. 모델 형성 / Compile - 다층 퍼셉트론(MLP) 모델
1) Sequential 모델
- 레이어를 순차적으로 쌓아 구성된 모델. 입력 데이터가 각 레이어를 순서대로 통과하며 출력값을 생성
- Sequential은 데이터가 순차적으로 흐르는 구조를 지원하기 때문에 MLP 외에도 CNN, RNN 등 다양한 네트워크를 만들 수 있음
- 하지만 Sequential은 복잡한 연결(병렬 구조, 다중 입력/출력 등)을 처리할 수 없으므로, 복잡한 모델에서는 Functional API나 Subclassing을 사용
2) 다층 퍼셉트론 (MLP, Multi-Layer Perceptron)
- 다층 퍼셉트론(MLP)은 인공신경망(ANN)의 기본 구조로, 완전 연결 레이어(Fully Connected Layer)가 여러 층으로 구성된 신경망
- 입력층 (Input Layer) : 입력 데이터를 모델로 전달. 데이터 차원에 따라 노드 수가 결정.
- 은닉층 (Hidden Layer) : 데이터의 패턴을 학습하는 레이어. 노드 수와 레이어 수는 사용자가 결정(하이퍼파라미터).
- 출력층 (Output Layer) : 최종 예측 값을 생성. 분류 문제에서는 클래스 개수만큼 노드가 있음.
- 활성화 함수로 비선형성을 추가해 복잡한 패턴 학습 가능. 일반적으로 ReLU, Tanh, Sigmoid 등이 사용됨.
3) 모델 컴파일
- 딥러닝에서 컴파일(compile)은 모델이 학습할 준비를 하는 과정으로, 손실 함수, 옵티마이저, 그리고 평가지표를 설정. 딥러닝 모델은 컴파일 후에 데이터를 학습하거나 평가
- 손실 함수
: 모델의 예측값과 실제값 간의 차이를 수치로 표현.
: 모델이 학습하면서 손실 값을 최소화하려고 노력 - 옵티마이저 (Optimizer)
: 가중치를 업데이트하여 손실을 최소화하는 알고리즘.
: 경사 하강법(Gradient Descent)을 기반으로 다양한 방식이 존재[Adam 옵티마이저]
: Adam(Adaptive Moment Estimation)은 경사 하강법의 변형 중 하나로, 학습률을 동적으로 조정하여 효율적인 학습을 수행
1) 작동 원리
- 1차 모멘트 (Mean) : 기울기의 이동 평균. 과거 기울기를 반영하여 학습 안정성 증가.
- 2차 모멘트 (Variance) : 기울기의 제곱에 대한 이동 평균. 학습률을 각 파라미터에 적응적으로 조정.
2) 장점
- 학습 속도가 빠르고, 복잡한 문제에서도 잘 작동.
- 학습률을 자동으로 조정하므로 별도의 튜닝 필요성이 적음.
- SGD, RMSProp, Momentum의 장점을 결합.
3) 파라미터
- learning_rate (기본값: 0.001): 학습 속도를 제어.
- beta_1 (기본값: 0.9): 1차 모멘트 추정의 기여도를 결정.
- beta_2 (기본값: 0.999): 2차 모멘트 추정의 기여도를 결정.
4) 적용 사례
- 대규모 데이터셋에서 효과적.
- 컴퓨터 비전, 자연어 처리, 시계열 분석 등 다양한 분야에서 사용. - 평가 지표 (Metrics)
: 모델의 성능을 평가하기 위해 사용하는 지표.
: 예: 분류 문제에서는 accuracy.
4) sparse_categorical_crossentropy 손실 함수
- 다중 클래스 분류 문제에서 사용되는 손실 함수.
- 레이블(y_train, y_test)이 정수로 된 경우(예: 0~9)에 사용
categorical_crossentropy
레이블이 원-핫 인코딩된 경우 사용.
예: [0, 1, 0, 0] 형태.
sparse_categorical_crossentropy:
레이블이 정수형인 경우 사용.
예: 클래스 레이블 1, 2, 3 등.
5) ReLU (Rectified Linear Unit)
- 입력 값 𝑥가 0보다 작으면 0, 𝑥가 0 이상이면 그대로 출력
- 기울기 소실 문제 완화: Sigmoid나 Tanh 같은 활성화 함수에서 발생하는 기울기 소실 문제를 줄임
- 학습이 빠르고, 심층 신경망에서도 잘 동작
- x가 음수인 경우 출력이 항상 0이므로 뉴런이 학습하지 않게 될 수 있음 (해결 : Leaky ReLU)
6) Softmax
- 출력층에서 주로 사용되는 활성화 함수로, 예측값을 확률 분포로 변환
- Softmax 함수는 입력 값을 지수화한 뒤, 그 값을 전체 합으로 나눔
- 각 출력값은 0~1 사이의 값을 가지며, 모든 출력의 합은 1
- 다중 클래스 분류 문제에서 적합
model = tf.keras.models.Sequential([
# Flatten : 2차원 입력 이미지를 1차원 벡터로 변환
# 출력 : 출력: 28 * 28 = 784 크기의 1차원 벡터.
tf.keras.layers.Flatten(input_shape=(28,28)),
# 완전 연결 레이어로, 1000개의 뉴런을 포함
# 활성화 함수: ReLU (Rectified Linear Unit)
tf.keras.layers.Dense(1000, activation='relu'),
# 출력 레이어로, 10개의 뉴런을 포함
# 활성화 함수: Softmax
tf.keras.layers.Dense(10, activation='softmax')])
model.summary()
# R :
Model: "sequential_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ flatten (Flatten) │ (None, 784) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_4 (Dense) │ (None, 1000) │ 785,000 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_5 (Dense) │ (None, 10) │ 10,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 795,010 (3.03 MB)
Trainable params: 795,010 (3.03 MB)
Non-trainable params: 0 (0.00 B)
# 모델 컴파일
model.compile(optimizer='adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
3. Model Fit
import time
start_time = time.time()
# batch_size=100 : 데이터를 100개씩 묶어서 학습
hist = model.fit(X_train, y_train, epochs=10,
batch_size=100, validation_data = (X_test, y_test))
print('---%s seconds ---' % (time.time() - start_time))
# R :
Epoch 10/10
600/600 ━━━━━━━━━━━━━━━━━━━━ 9s 14ms/step - accuracy: 0.9970 - loss: 0.0092 - val_accuracy: 0.9811 - val_loss: 0.07154. Loss , Accuracy 시각화
- loss: 학습 데이터에서 계산된 손실 값.
- val_loss: 검증 데이터에서 계산된 손실 값.
- accuracy: 학습 데이터에서의 정확도.
- val_accuracy: 검증 데이터에서의 정확도.
import matplotlib.pyplot as plt
plot_target = ['loss', 'val_loss', 'accuracy', 'val_accuracy']
plt.figure(figsize=(8,4))
for each in plot_target:
plt.plot(hist.history[each], label=each)
plt.legend()
plt.grid()
plt.show()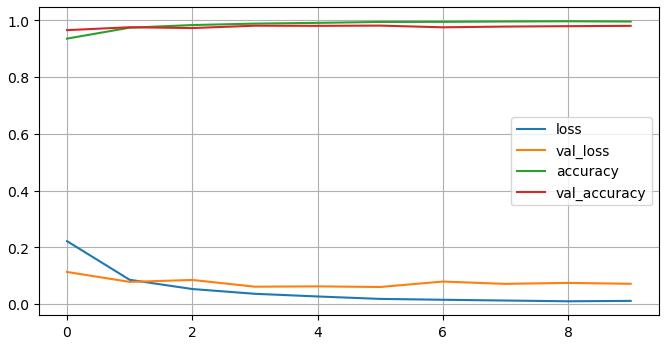
5. 모델 평가 / 예측 결과 분석 / 잘못 예측된 샘플
## 모델 평가
score = model.evaluate(X_test, y_test, verbose=0)
print('Test loss: ', score[0])
print('Test accuracy ', score[1])
# R :
Test loss: 0.071492999792099
Test accuracy 0.9811000227928162
## 예측 결과 분석
import numpy as np
# 테스트 데이터를 모델에 전달하여 각 샘플에 대한 클래스별 확률 분포를 반환
# 출력: (n,10) 형태의 배열 (n은 테스트 데이터의 샘플 수).
predicted_result = model.predict(X_test)
predicted_labels = np.argmax(predicted_result, axis=1)
predicted_labels[:10]
# R :
array([7, 2, 1, 0, 4, 1, 4, 9, 5, 9], dtype=int64)
# 참고
predicted_result
# r :
array([[9.7913115e-11, 2.5638023e-11, 4.5554724e-09, ..., 9.9999928e-01,
1.8270248e-08, 1.2828988e-07],
[1.0676701e-12, 3.3511853e-08, 1.0000000e+00, ..., 2.6424673e-17,
5.2285447e-11, 1.3216238e-17],
[6.8583687e-11, 9.9999535e-01, 2.5189806e-07, ..., 3.2634623e-06,
7.7177970e-07, 2.6368216e-09],
..., dtype=float32)
predicted_labels
# r :
array([7, 2, 1, ..., 4, 5, 6], dtype=int64)
## 잘못 예측된 샘플
wrong_result = []
for n in range(0, len(y_test)):
if predicted_labels[n] != y_test[n]:
wrong_result.append(n)
len(wrong_result)
# r :
189
import random
# wrong_result 리스트에서 임의의 16개 샘플을 선택
samples = random.choices(population=wrong_result, k=16)
samples
# r :
[4504,
9679,
3838,
3926,
2369,
6597,
1156,
2004,
3289,
4578,
1242,
7451,
1112,
5457,
3405,
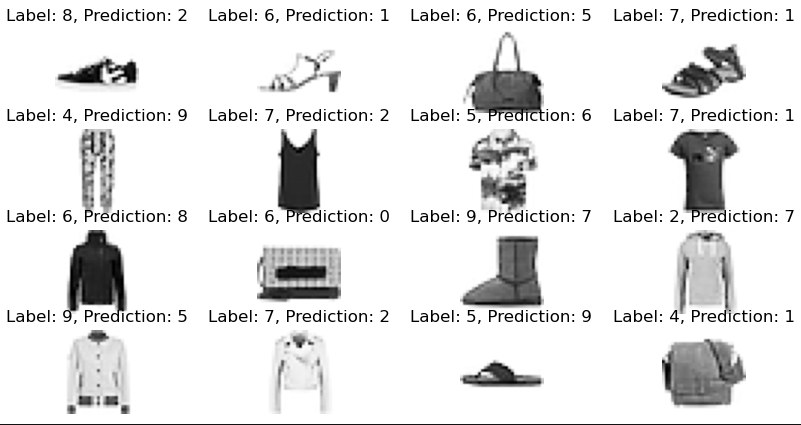
6576]6. 잘못 예측된 샘플 시각화
plt.figure(figsize=(10,5))
for index, n in enumerate(samples):
plt.subplot(4,4,index+1)
plt.imshow(X_test[n].reshape(28,28), cmap='Greys')
plt.title('Label: ' + str(y_test[n]) + ', Prediction: ' + str(predicted_labels[n]))
plt.axis('off')
plt.show()
MNIST - CNN
1. 데이터 불러오기 / 전처리
from tensorflow.keras import datasets
mnist = datasets.mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# 데이터 정규화
# 각 픽셀 값을 0~1 사이의 실수로 정규화
X_train, X_test = X_train/255. , X_test/255.
# CNN에 적합한 4D 텐서로 변환
# CNN 모델은 입력 데이터를 (샘플 수, 높이, 너비, 채널 수) 형식으로 받음
X_train = X_train.reshape(X_train.shape[0], 28,28,1)
X_test = X_test.reshape(X_test.shape[0], 28,28,1)2. CNN 모델 적용
- 합성곱: 특징 추출 (패턴, 에지 등).
- 풀링: 차원 축소 및 중요한 정보 유지.
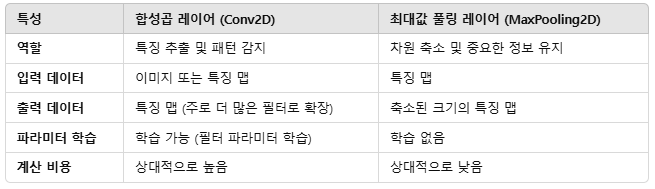
1) 합성곱 레이어 (Convolutional Layer)
-
합성곱 레이어는 이미지 데이터에서 중요한 공간적 패턴(예: 가장자리, 모양 등)을 학습하기 위해 사용. 이는 입력 데이터에 필터(filter)를 적용하여 특징 맵(feature map)을 생성하는 과정
-
필터(Filter, Kernel)
: 합성곱 레이어에서 사용하는 작은 행렬.
: 일반적으로 크기는 3×3, 5×5 등
: 필터는 입력 이미지 위를 슬라이딩하며 특정 패턴을 감지. -
합성곱 연산
: 필터와 입력 이미지의 부분 영역 간 요소별 곱(element-wise multiplication)을 계산한 뒤 합산.
: 이 결과는 특징 맵(Feature Map)의 한 픽셀이 됨
: 필터가 슬라이딩하면서 전체 이미지를 처리하여 특징 맵을 생성. -
패딩 (Padding):
'same': 입력 크기를 유지하기 위해 테두리에 0을 추가.
'valid': 패딩 없이 순수하게 합성곱 수행. -
스트라이드 (Stride):
: 필터가 이동하는 간격.
: 기본값은 1, 스트라이드가 커지면 출력 크기가 작아짐
2) 최대값 풀링 레이어 (MaxPooling Layer)
-
최대값 풀링은 입력 데이터의 공간 크기를 줄이고, 중요한 정보를 추출하여 계산량을 줄이는 데 사용. 입력 영역에서 최대값만 추출하는 방식
-
풀링 크기 (Pool Size):
: 풀링 레이어는 작은 윈도우를 정의하여 입력 데이터를 축소.
: 일반적으로 2×2 또는 3×3 크기의 윈도우를 사용. -
스트라이드 (Stride):
: 풀링 윈도우가 이동하는 간격.
: 보통 스트라이드 크기를 풀링 크기와 동일하게 설정 (2×2 풀링 → 스트라이드 2). -
작동 방식:
: 풀링 윈도우 내에서 가장 큰 값을 추출(최대값).
: 각 윈도우의 최대값으로 출력 배열 구성. -
장점 :
: 차원 축소 = 입력 데이터의 공간 크기를 줄여 계산량 감소.
: 특징 강조 = 중요한 정보(최대값)를 유지하여 특징 맵의 의미 있는 정보 전달.
: 과적합 방지 = 입력 크기를 줄여 파라미터 수를 감소시켜 과적합 방지.
import tensorflow as tf
model = tf.keras.models.Sequential([
# 1. 합성곱 레이어 1
# Conv2D: 이미지에서 특징을 추출하는 합성곱 레이어
# 32 filters: 32개의 필터를 사용하여 32개의 특징 맵을 생성
# Kernel size (5, 5): 필터 크기
# Strides (1, 1): 필터 이동 단위
# Padding 'same': 출력 크기가 입력 크기와 같도록 패딩 추가
tf.keras.layers.Conv2D(32, kernel_size=(5,5), strides=(1,1),
padding='same', activation='relu',
input_shape=(28,28,1)),
# 2. 최대 풀링 레이어 1
# MaxPooling2D: 최대값 풀링으로 공간 크기를 줄이고 특징을 강조
# Pool size (2, 2): 2x2 영역에서 최대값 추출
# Strides (2, 2): 2픽셀씩 이동
tf.keras.layers.MaxPooling2D((2,2), strides=(2,2)),
# 3. 합성곱 레이어 2
# 64개의 필터를 사용하여 더 많은 특징을 추출.
tf.keras.layers.Conv2D(64, kernel_size=(2,2), strides=(1,1),
activation='relu', padding='same'),
# 4. 최대 풀링 레이어 2
# 두 번째 풀링 레이어로 공간 크기를 추가로 축소.
tf.keras.layers.MaxPooling2D((2,2), strides=(2,2)),
# 5. 드롭아웃 레이어
# 랜덤하게 25%의 뉴런을 학습에서 제외하여 과적합 방지.
tf.keras.layers.Dropout(0.25),
# 6. 플래튼 레이어
# 2D 형태의 데이터를 1D 벡터로 변환하여 Dense 레이어에 전달
tf.keras.layers.Flatten(),
# 7. 완전 연결(Dense) 레이어
# 완전 연결 레이어로, 1000개의 뉴런 사용
# ReLU 활성화 함수로 비선형성을 추가하여 복잡한 패턴 학습
tf.keras.layers.Dense(1000, activation='relu'),
# 8. 출력 레이어
# 출력 레이어로, 10개의 뉴런 사용
# Softmax 활성화 함수로 각 클래스의 확률 반환
tf.keras.layers.Dense(10, activation='softmax')
])
model.summary()
# r :
Model: "sequential_4"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ conv2d_3 (Conv2D) │ (None, 28, 28, 32) │ 832 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_2 (MaxPooling2D) │ (None, 14, 14, 32) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ conv2d_4 (Conv2D) │ (None, 14, 14, 64) │ 8,256 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ max_pooling2d_3 (MaxPooling2D) │ (None, 7, 7, 64) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout (Dropout) │ (None, 7, 7, 64) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ flatten_3 (Flatten) │ (None, 3136) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_10 (Dense) │ (None, 1000) │ 3,137,000 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_11 (Dense) │ (None, 10) │ 10,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 3,156,098 (12.04 MB)
Trainable params: 3,156,098 (12.04 MB)
Non-trainable params: 0 (0.00 B)3. Model Compile / Fit / Loss , Accuracy 시각화
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
hist = model.fit(X_train, y_train, epochs=5, validation_data=(X_test, y_test))
# r :
Epoch 5/5
1875/1875 ━━━━━━━━━━━━━━━━━━━━ 117s 62ms/step - accuracy: 0.9948 - loss: 0.0174 - val_accuracy: 0.9904 - val_loss: 0.0300
import matplotlib.pyplot as plt
plot_target = ['loss','val_loss', 'accuracy', 'val_accuracy']
plt.figure(figsize=(10,5))
for each in plot_target:
plt.plot(hist.history[each], label=each)
plt.legend()
plt.grid()
plt.show()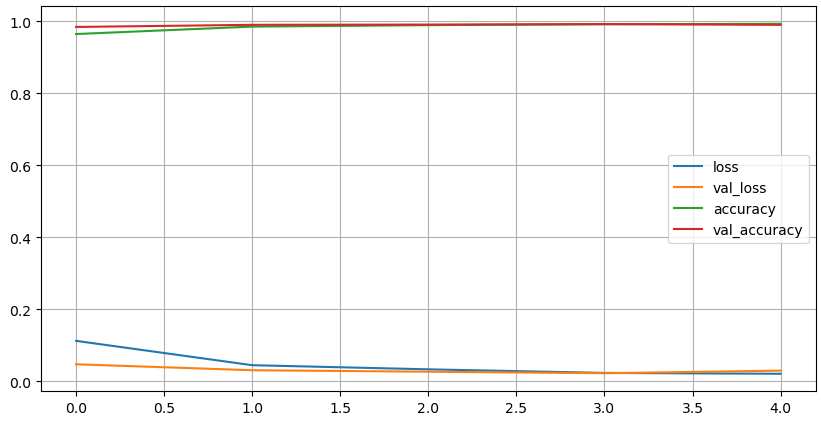
Model Evaluate / 잘못 예측된 샘플 시각화
model.evaluate(X_test, y_test)
# r :
[0.0300475861877203, 0.9904000163078308]
import numpy as np
predicted_result = model.predict(X_test)
predicted_labels = np.argmax(predicted_result, axis=1)
predicted_labels[:10]
# r :
array([7, 2, 1, 0, 4, 1, 4, 9, 5, 9], dtype=int64)
wrong_result = []
for n in range(len(y_test)):
if predicted_labels[n] != y_test[n]:
wrong_result.append(n)
len(wrong_result)
# r : 96
import random
samples = random.choices(population=wrong_result, k=16)
samples
# r :
[582,
4699,
1014,
1039,
1924,
5654,
9729,
1260,
4571,
4814,
1554,
9664,
2939,
9024,
5997,
7574]
plt.figure(figsize=(10,5))
for index, n in enumerate(samples):
plt.subplot(4,4,index+1)
plt.imshow(x_test[n].reshape(28,28), cmap='Greys')
plt.title('Label: ' + str(y_test[n]) + ', Prediction: ' + str(predicted_labels[n]))
plt.axis('off')
plt.show()