기초수학 순열

1. 순열

순열은 n개에서 r개를 택하여 순서있게 나열하는 경우의 수를 말한다.

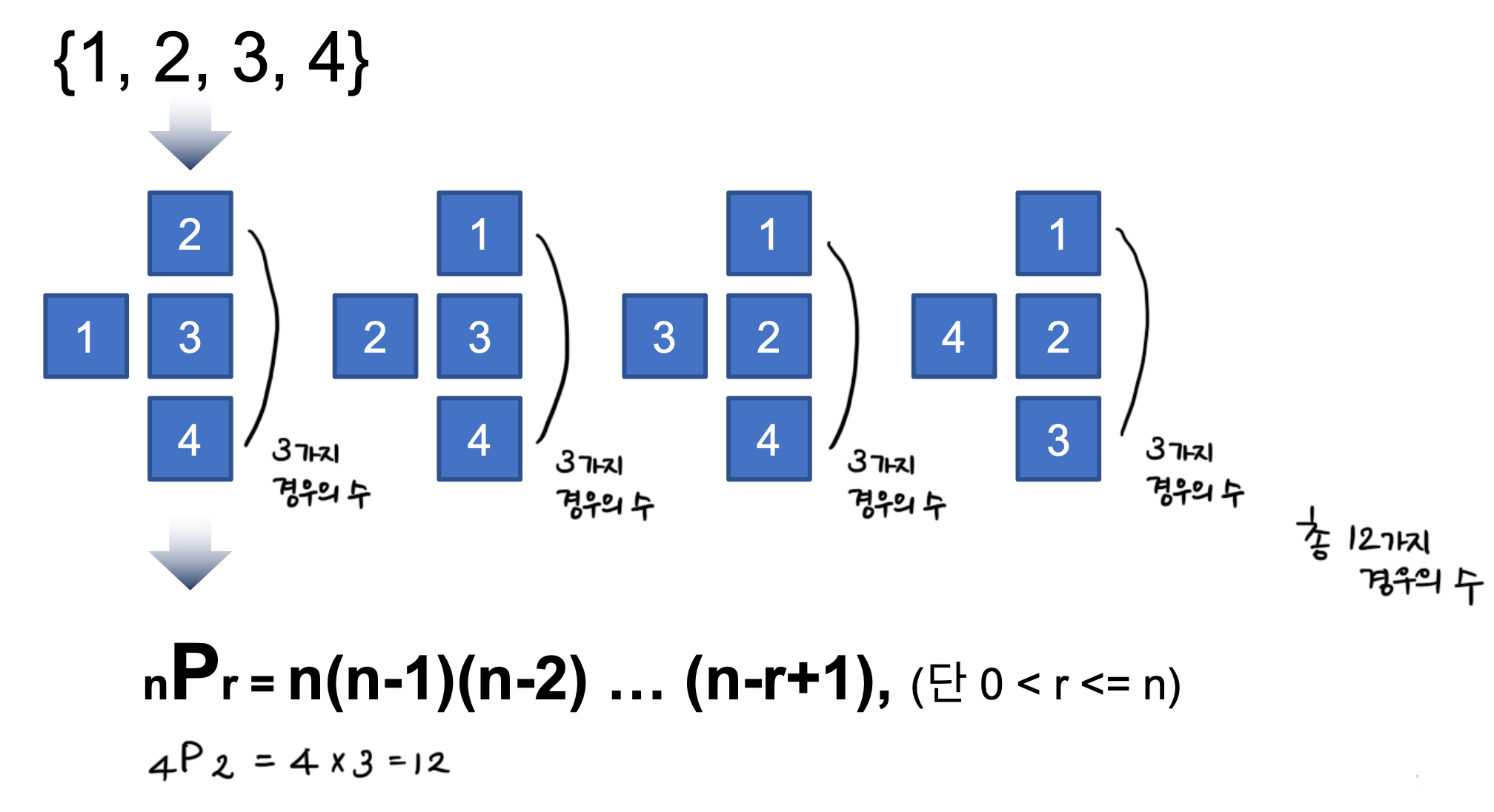
• n: 모든 항의 개수
• P: permutation의 약자
• r: 몇 개

1.1 순열과 팩토리얼

순열은 팩토리얼(계승)을 이용해서 나타낼 수 있다.

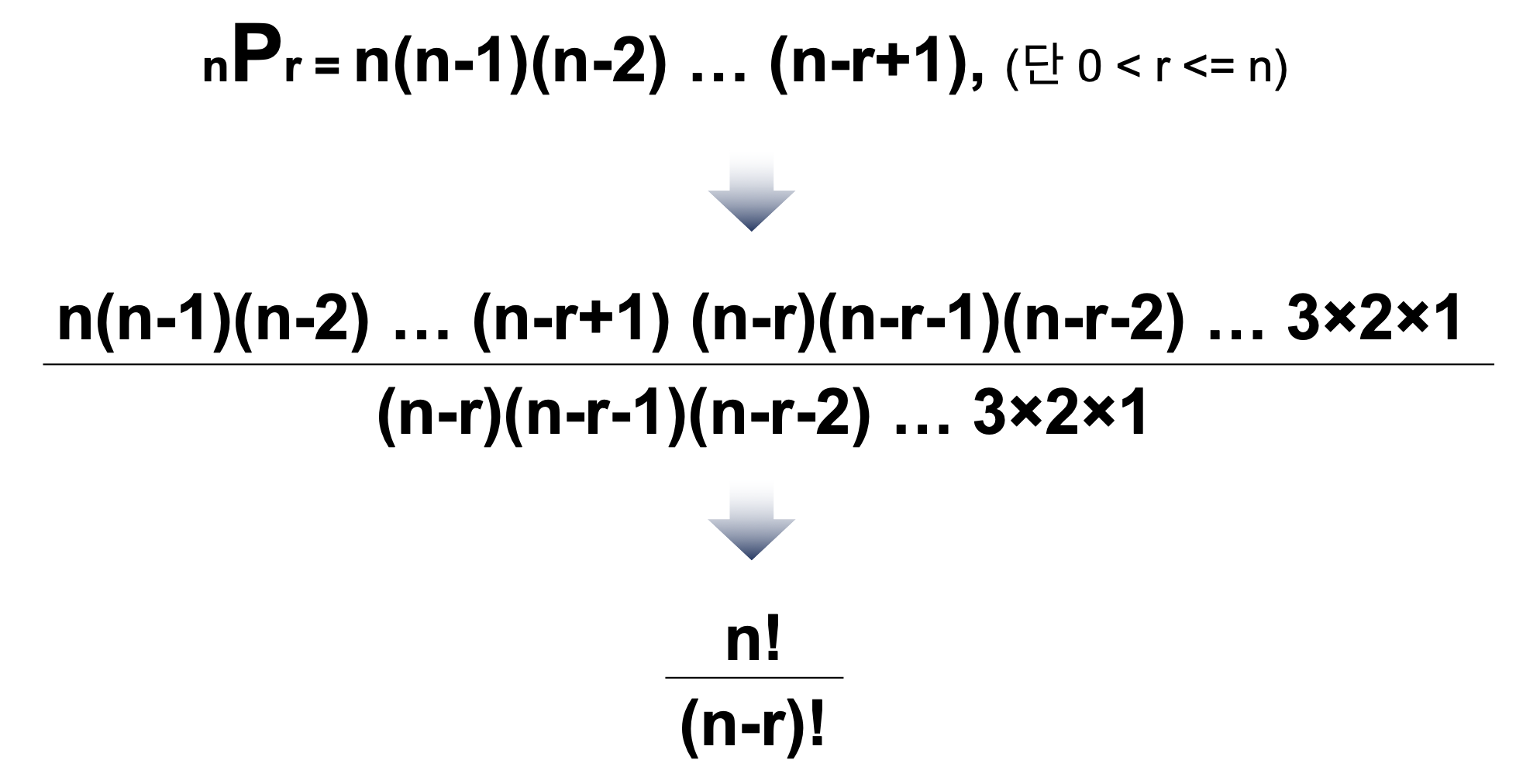
Example 1: 다음 순열의 값 구하기

• 8P3
• 7P5

1) 순열 공식:

8P3 = 8 x 7 x (5+1) = 8 x 7 x 6 = 336

7P5 = 7 x 6 x 5 x 4 x (2+1) = 7 x 6 x 5 x 4 x 3 = 2520

2) 팩토리얼 공식:

8! / 5! = (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (5 x 4 x 3 x 2 x 1) = 8 x 7 x 6 = 336

7! / 2! = (7 x 6 x 5 x 4 x 3 x 2 x 1) / (2 x 1) = 7 x 6 x 5 x 4 x 3 = 2520

Example 2: 카드 4장을 일렬로 나열하되 삼각형과 사각형이 서로 이웃하도록 나열하는 경우의 수 구하기

삼각형과 사각형이 서루 이웃이 되도록 나열을 해야하기에 두개의 카드를 묶으면 카드 4장에서 총 3장이 된다.

총 3장의 경우의 수 = 3! = 3 x 2 x 1 = 6

서로 이웃이된 삼각형과 사각형은 (1) 삼각형, 사각형, (2) 사각형, 삼각형 순으로 나열될 수 있다.

이웃이된 삼각형과 사각형의 경우의 수 = 2! = 2 x 1 = 2

1.2 Python을 이용한 순열

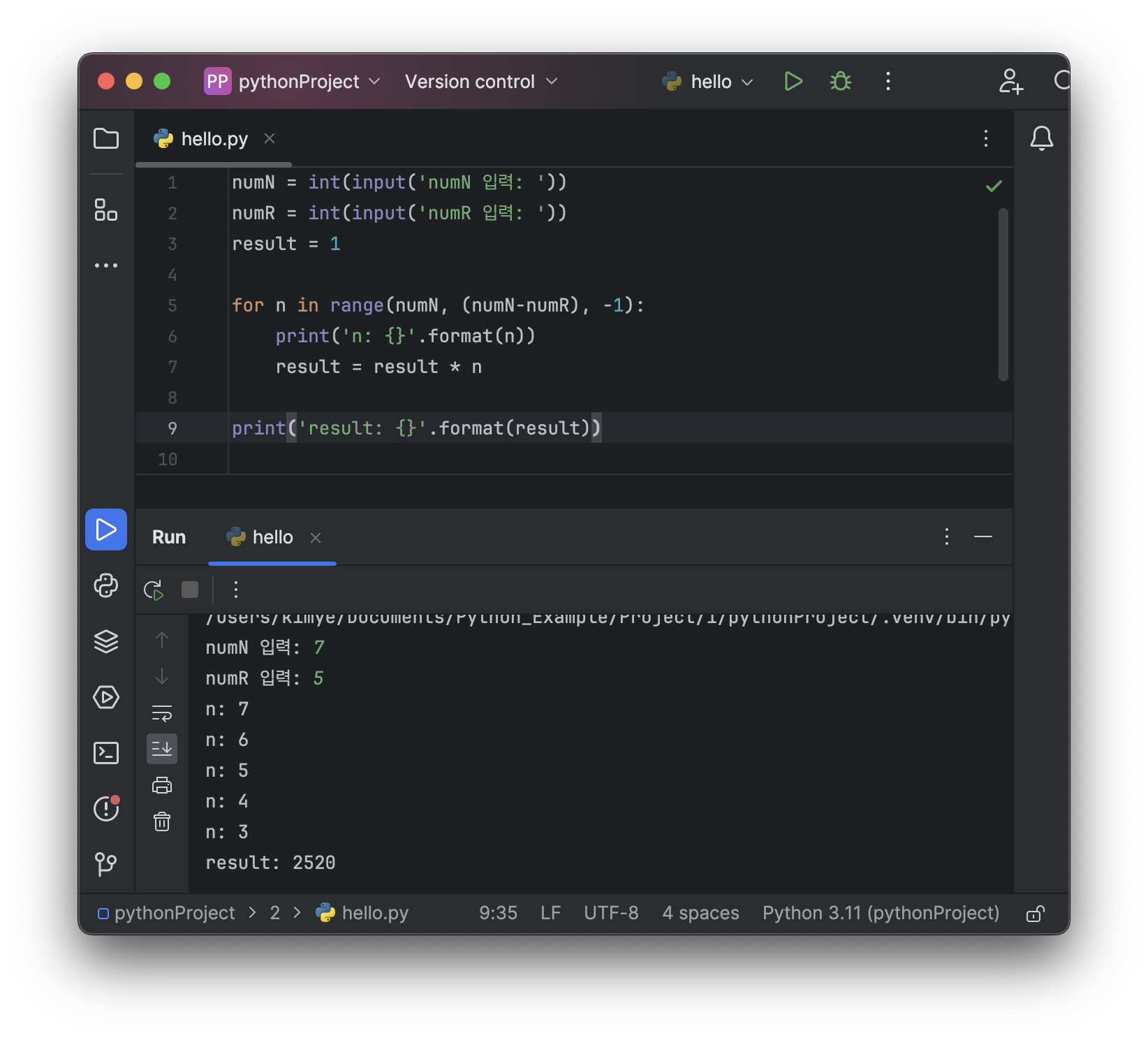
Example 1: Python을 이용해서 다음 순열들의 값을 구하는 프로그램 만들기

• 8P3
• 7P5

numN = int(input('numN 입력: '))
numR = int(input('numR 입력: '))
result = 1

for n in range(numN, (numN-numR), -1):
    print('n: {}'.format(n))
    result = result * n

print('result: {}'.format(result))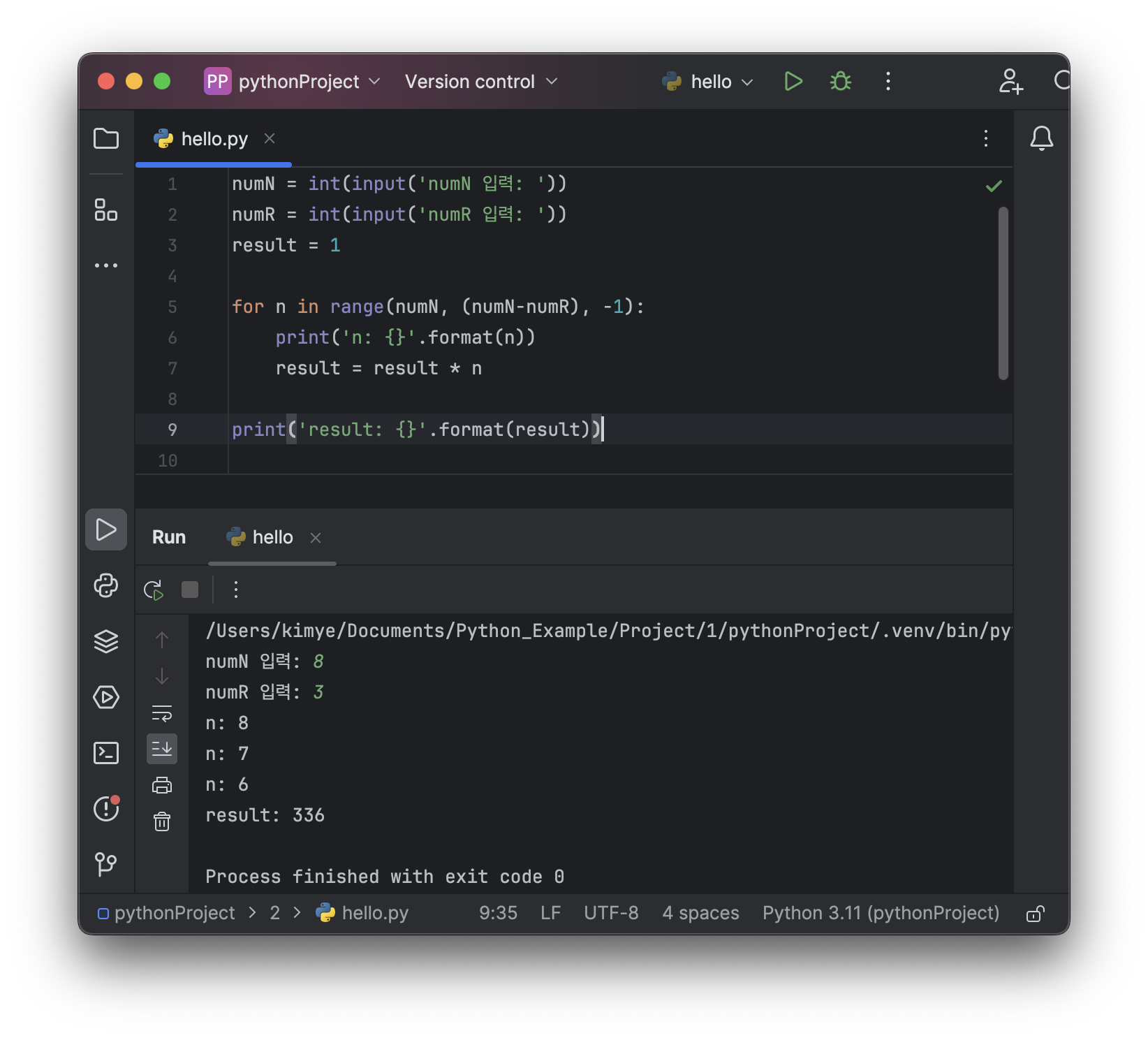

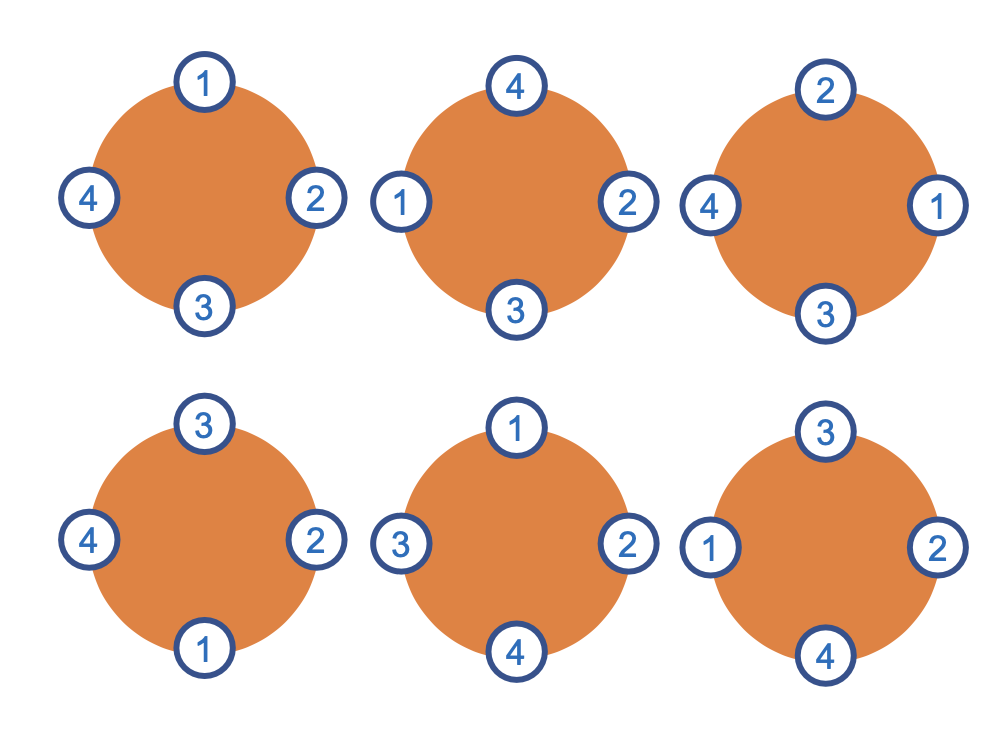
2. 원 순열

원 수열은 시작과 끝의 구분이 없는 순열을 말한다.

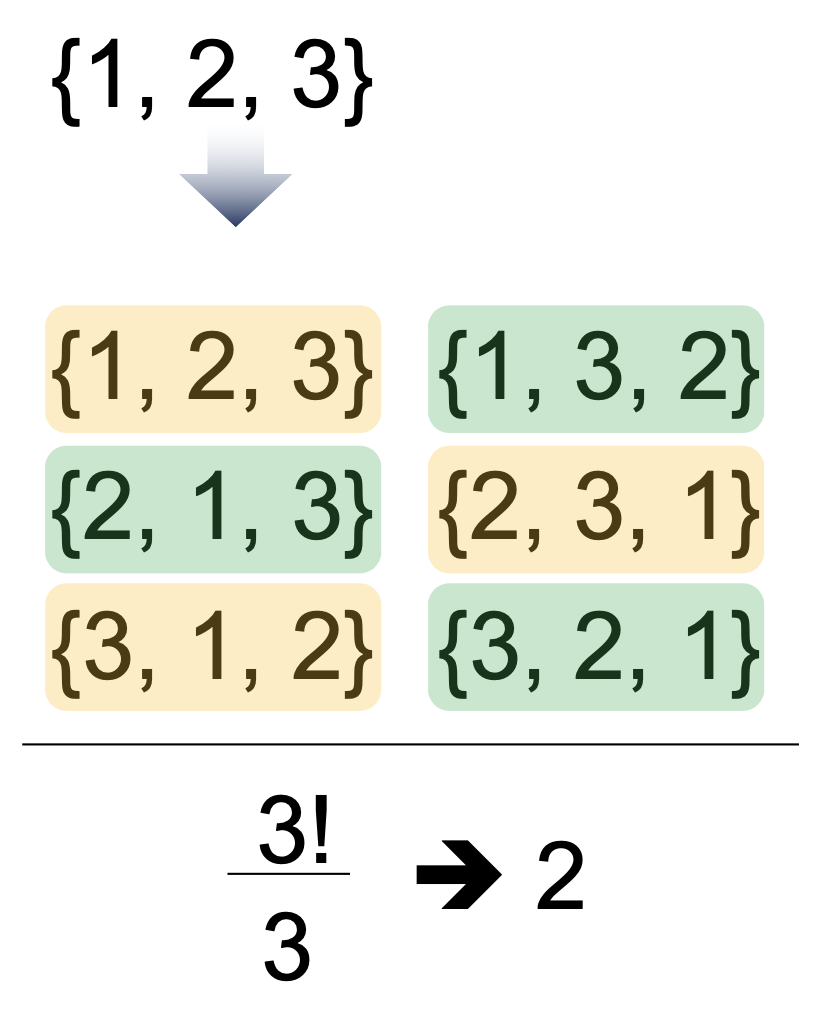
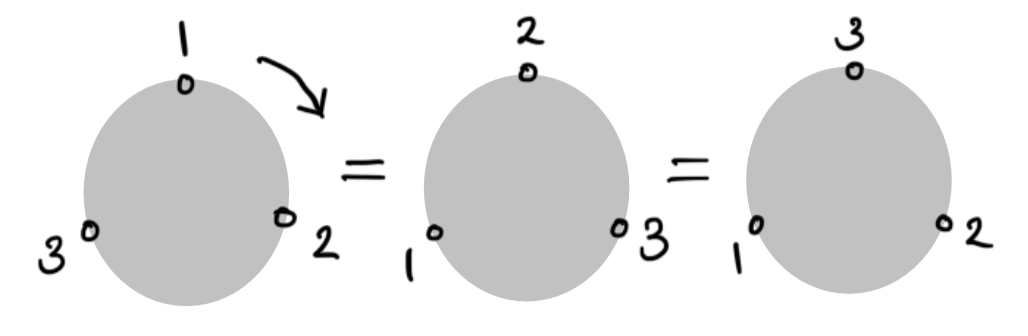
원 수열 공식

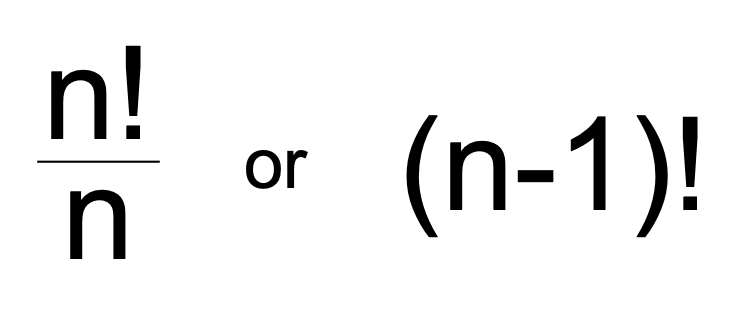
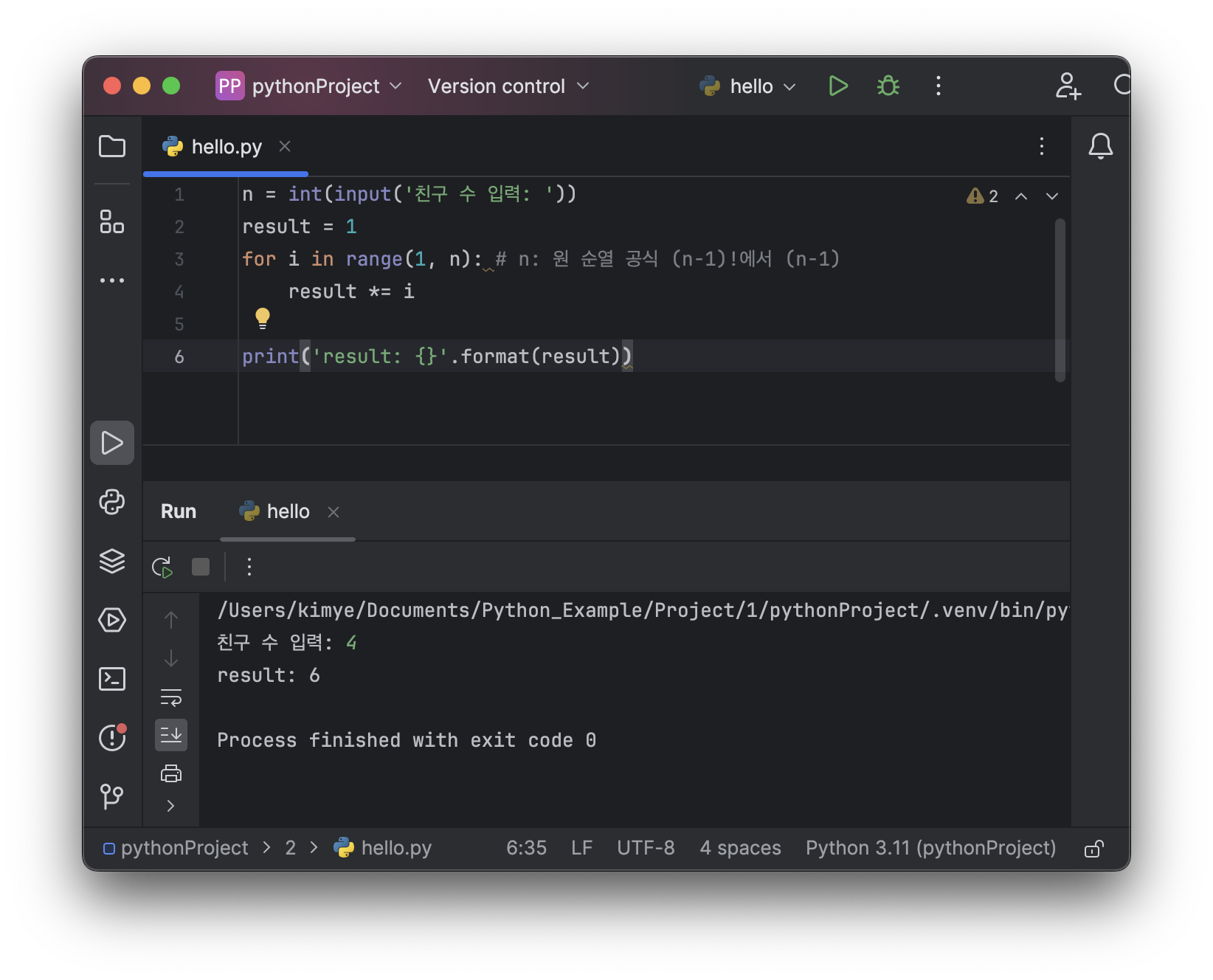
Example: 4명의 친구가 원탁 테이블에 앉을 수 잇는 순서를 계산하기

n = int(input('친구 수 입력: '))
result = 1
for i in range(1, n): # n: 원 순열 공식 (n-1)!에서 (n-1)
    result *= i

print('result: {}'.format(result))