기초수학 조합

1. 조합

조합은 n개에서 r개를 택하는 경우의 수이다.

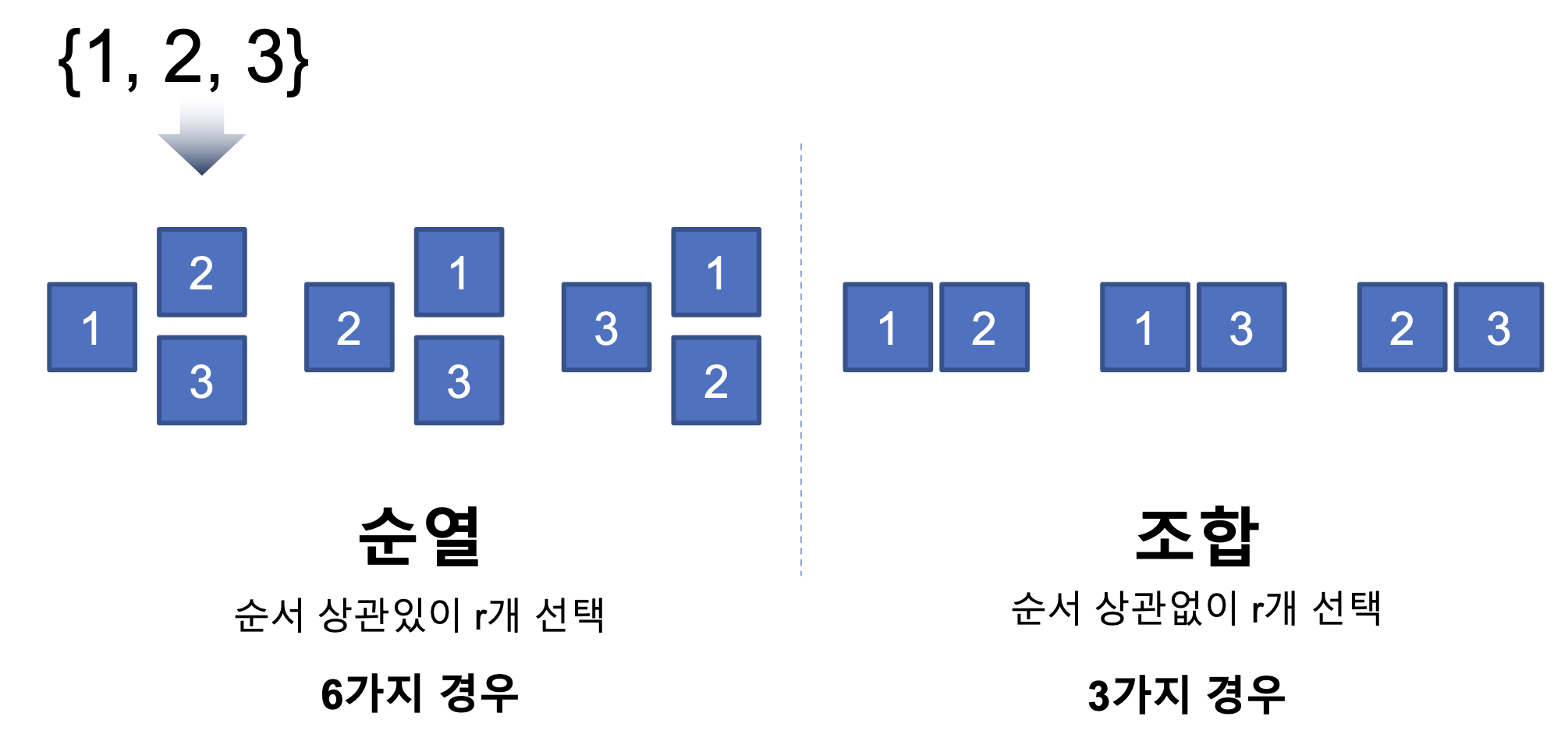
Example: 4개에서 3개를 택하는 경우의 수

1) 순열: 24가지 경우의 수

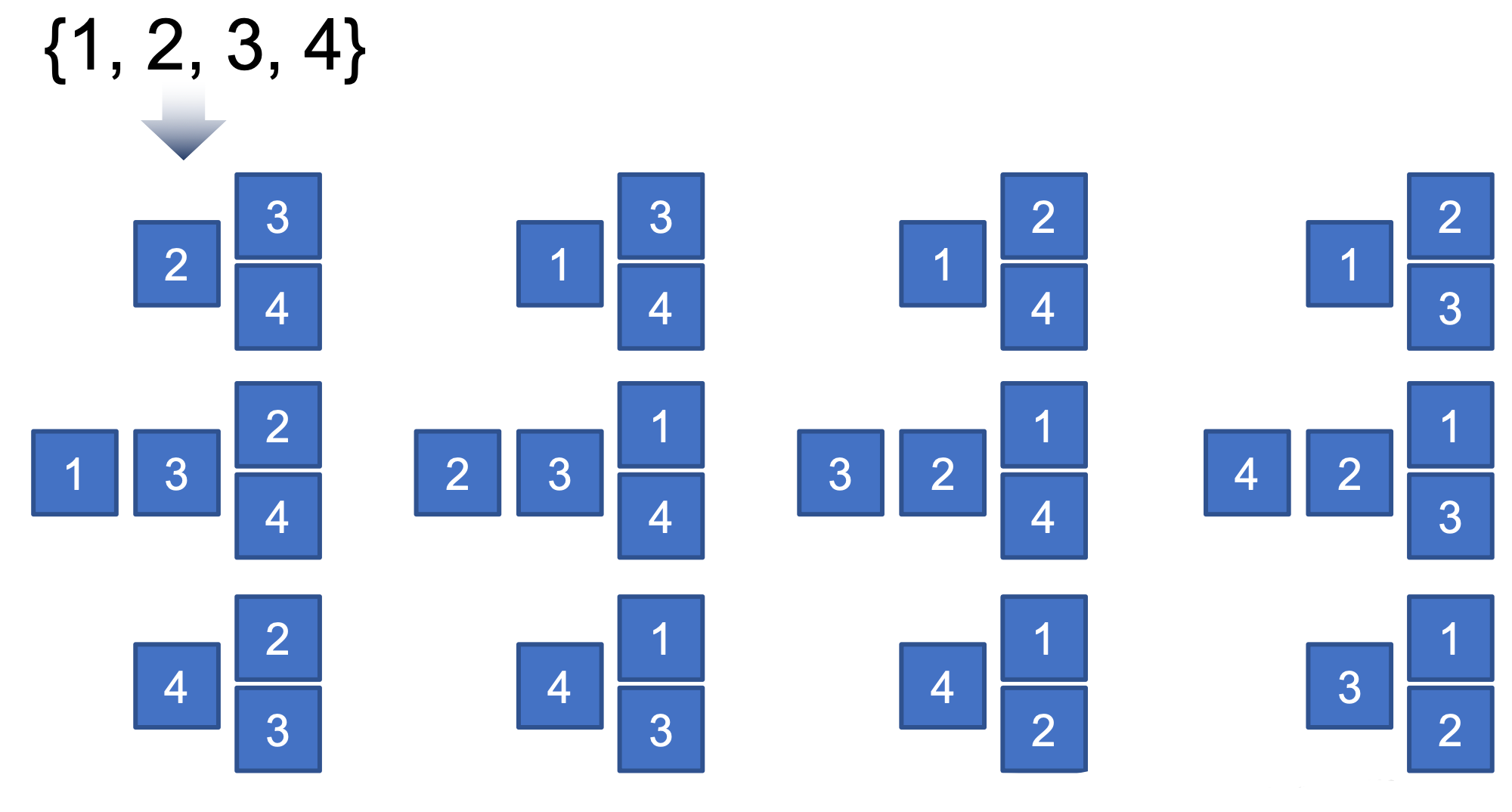
2) 조합: 4가지 경우의 수

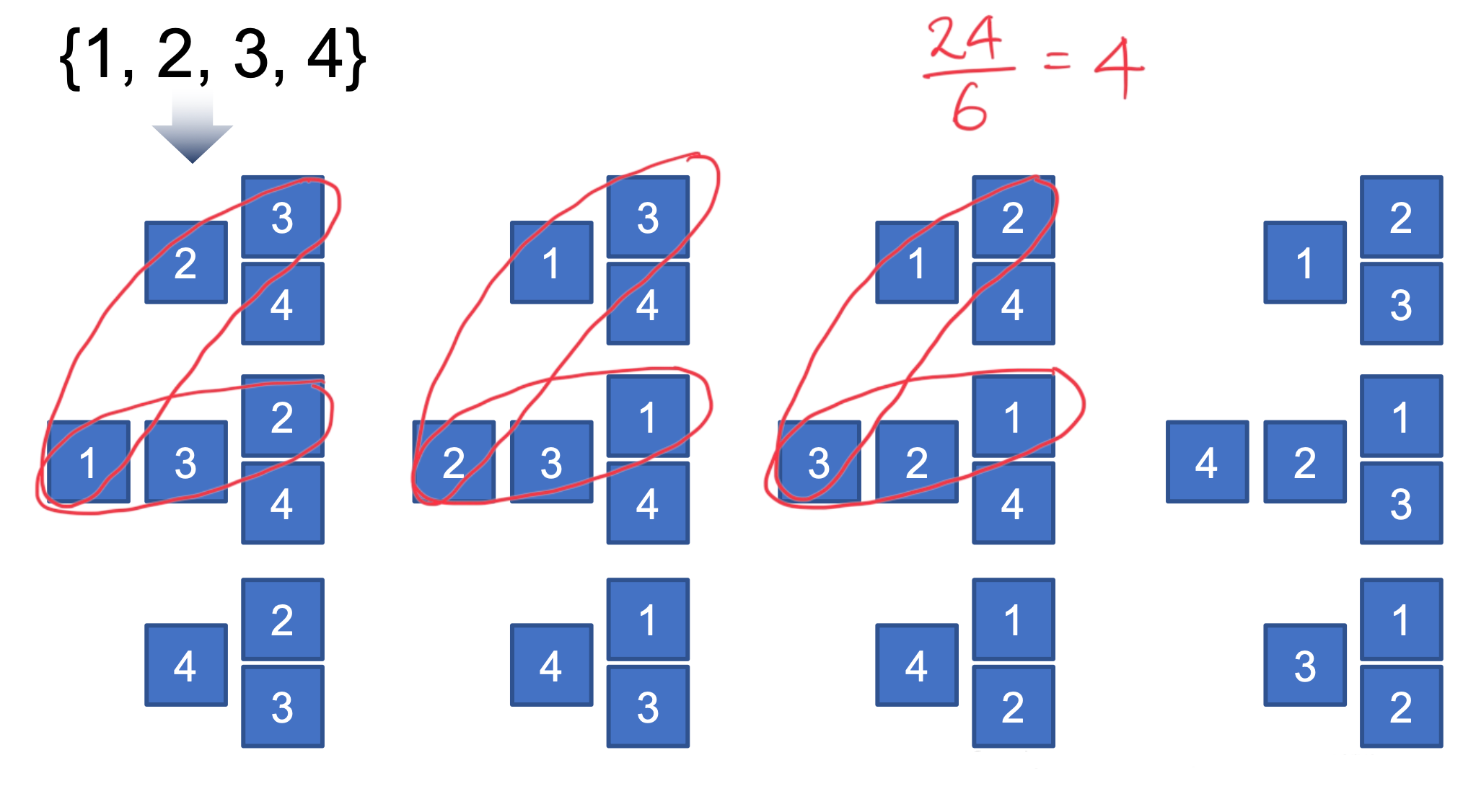
1.1 순열과 조합

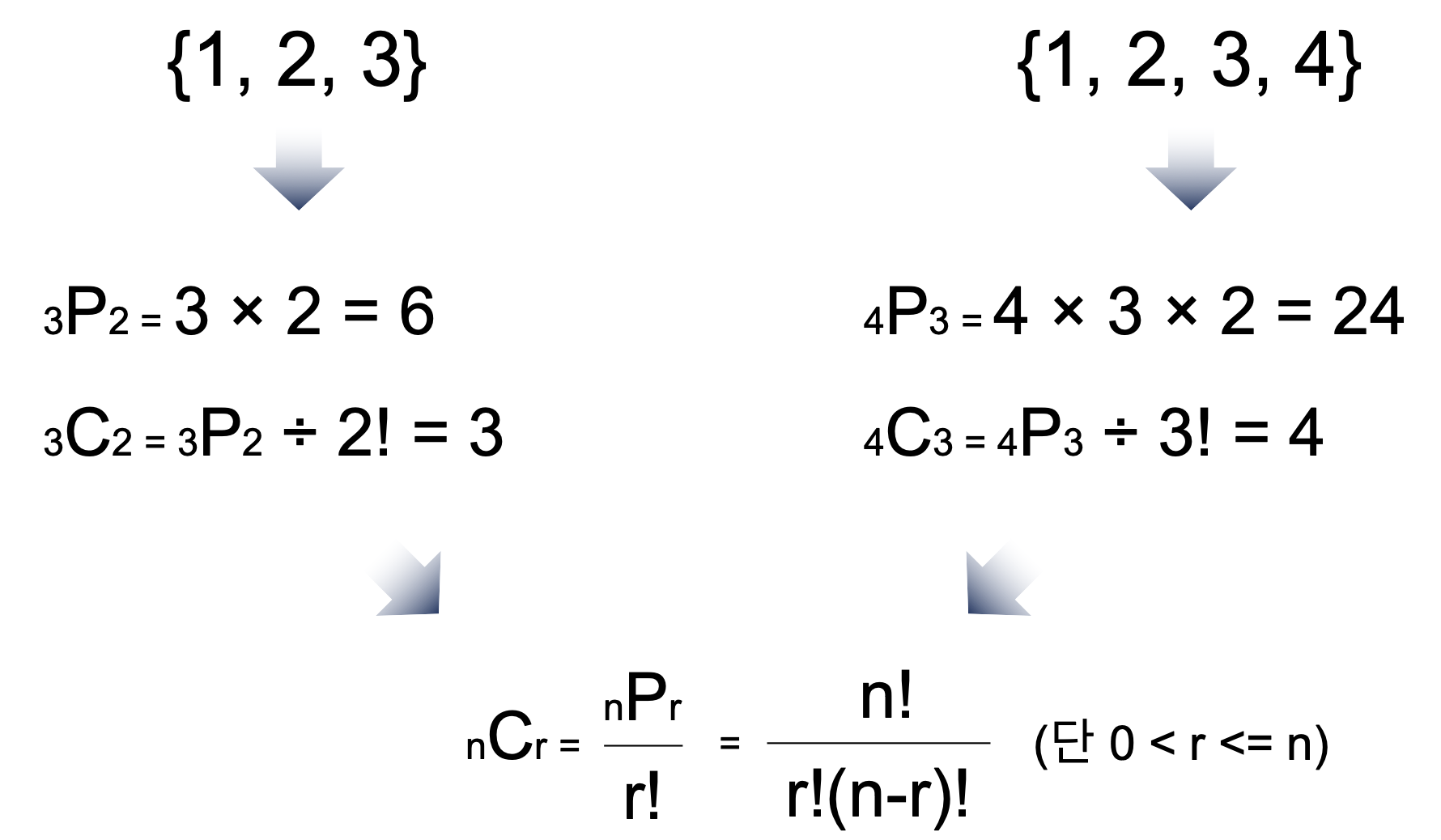
• C: combination의 약자

Example 1: 다음 조합의 값 구하기

8C3

1) nPr / r!

8 x 7 x (5+1) / 3! = (8 x 7 x 6) / (3 x 2 x 1) = 56

2) n! / r!(n-r)!

8! / 3!(8-3)! = 8! / (3! x 5!) = (8 x 7 x 6 x 5 x 4 x 3 x 2 x 1) / (3 x 2 x 1)(5 x 4 x 3 x 2 x 1) = (8 x 7 x 6) / (3 x 2 x 1) = 56

Example 2: 다음 조합의 값 구하기

7C5

1) nPr / r!

7 x 6 x 5 x 4 x (2+1) / 5! = (7 x 6 x 5 x 4 x 3) / (5 x 4 x 3 x 2 x 1) = (7 x 6) / 2 = 21

2) n! / r!(n-r)!

7! / 5!(7-5)! = 7! / 5! x 2! = (7 x 6 x 5 x 4 x 3 x 2 x 1) / (5 x 4 x 3 x 2 x 1)(2 x 1) = (7 x 6) / 2 = 21

Example 3: 카드 5장 중 2장을 선택했을 때 삼각형과 사각형이 동시에 선택될 수 있는 확률 구하기

5C2 = 5! / 2!(5-2)! = (5 x 4 x 3 x 2 x 1) / (2 x 1)(3 x 2 x 1) = (5 x 4) / 2 = 10

카드 5장 중 2장을 선택했을 때 10가지 경우의 수가 나온다. 그 중에서 2장의 카드가 삼각형과 사각형이 동시에 선택될 수 있는 확률은 10개 중 1개 이므로 10%의 확률이 있다.

1.2 Python을 이용한 조합

Example 1: Python을 이용해서 다음 조합들의 값을 구하는 프로그램 만들기

1) 8C3

numN = int(input('numN 입력: '))
numR= int(input('numR 입력: '))

resultP = 1 # 순열 값
resultR = 1 # r!
resultC = 1 # 조합 값

for n in range(numN, (numN - numR), -1):
    print('n: {}'.format(n))
    resultP = resultP * n

print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    print('n: {}'.format(n))
    resultR = resultR * n

print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC))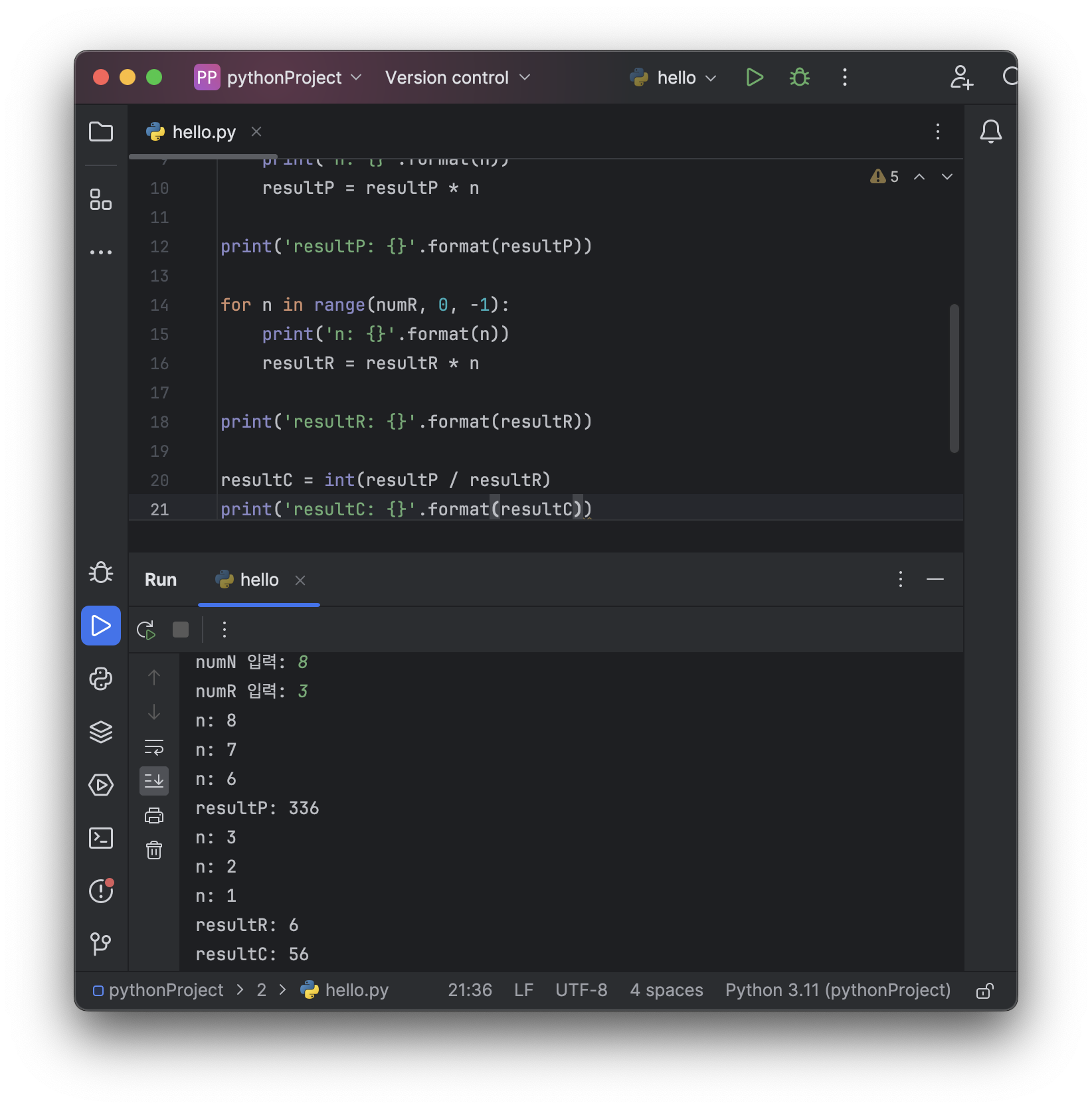

2) 7C5

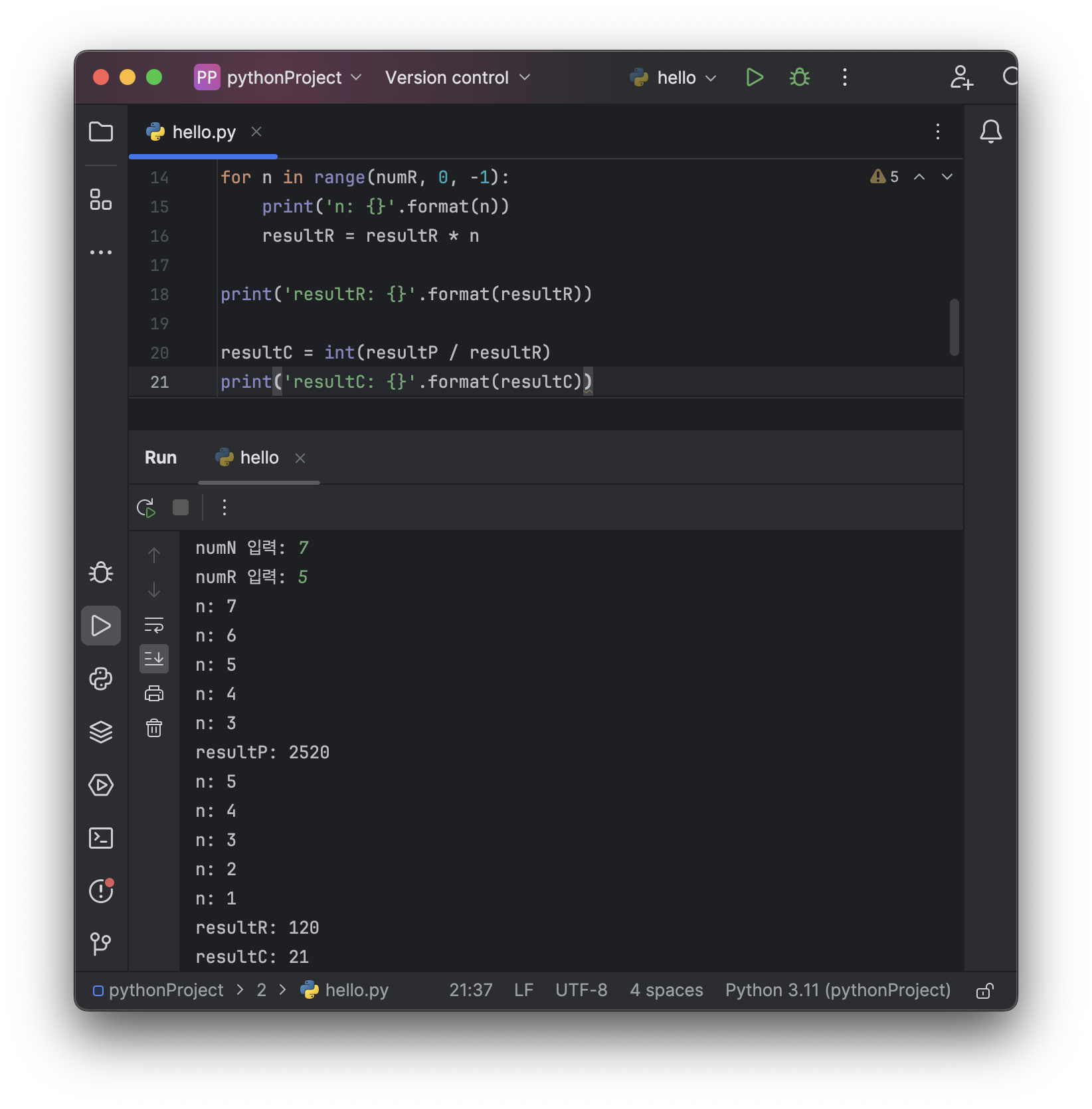
Example 2: 카드 5장 중 2장을 선택했을 때 삼각형과 사각형이 동시에 선택될 수 있는 확률 구하기

#5C2

numN = int(input('numN 입력: '))
numR= int(input('numR 입력: '))

resultP = 1 # 순열 값
resultR = 1 # r!
resultC = 1 # 조합 값

for n in range(numN, (numN - numR), -1):
    print('n: {}'.format(n))
    resultP = resultP * n

print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    print('n: {}'.format(n))
    resultR = resultR * n

print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC))

result = 1/resultC * 100
print('{}%'.format(round(result, 2)))