기초수학 확률

1. 확률

확률은 모든 사건에서 특정 사건이 일어날 수 있는 수를 나타낸 것이다.

예시 1: 동전

• 모든 사건: 앞, 뒤 ➞ 2가지 경우
• 특정 사건: 앞 ➞ 1가지 경우, 뒤 ➞ 1가지 경우
• 확률: 앞 ➞ 1/2, 뒤 ➞ 1/2

예시 2: 주사위

• 모든 사건: 1, 2, 3, 4, 5, 6 ➞ 6가지 경우
• 특정 사건: 1 ➞ 1가지 경우, 2 ➞ 1가지 경우, 3 ➞ 1가지 경우, 4 ➞ 1가지 경우, 5 ➞ 1가지 경우, 6 ➞ 1가지 경우
• 확률: 1 ➞ 1/6, 2 ➞ 1/6, 3 ➞ 1/6, 4 ➞ 1/6, 5 ➞ 1/6, 6 ➞ 1/6

확률 용어

모든 사건 ➞ 표본 공간 (sample)
특정 사건 ➞ 사건 (event)

1.1 확률과 조합

조합을 이용해서 확률을 알아낼 수 있다.

Example 1: 박스에 '꽝'이 적힌 종이가 4장 있고, '선물'이 적힌 종이가 3장 있다. 3장을 뽑을 경우 다음 경우의 수 구하기

7C3 = 7! / 3!(7-3)! = 7! / (3! x 4!) = (7 x 6 x 5 x 4 x 3 x 2 x 1) / (3 x 2 x 1)(4 x 3 x 2 x 1) = (7 x 6 x 5) / (3 x 2 x 1) = 35

1) 꽝: 0, 선물: 3

3C3 = 3! / 3!(3-3)! = 3! / 3! = 1

꽝: 0, 선물: 3의 확률 = 1/35

2) 꽝: 1, 선물: 2

4C1 x 3C2 = (4! / 1!(4-1)!) x (3! / 2!(3-2)!) = (4! / 3!) x (3! / (2! x 1!) = 4 x 3 = 12

꽝: 1, 선물: 2의 확률: 12/35

3) 꽝: 2, 선물: 1

4C2 x 3C1 = (4! / 2!(4-2)!) x (3! / 1!(3-1)!) = (4! / (2! x 2!)) x (3! / (1! x 2!)) = ((4 x 3) / 2!) x 3 = 6 x 3 = 18

꽝: 2, 선물: 1의 확률: 18/35

4) 꽝: 3, 선물: 0

4C3 x 3C0 = (4! / 3!(4-3)!) x (3! / 3!) = (4! / 3!) = 4

꽝: 3, 선물: 0의 확률: 4/35

Example 2: 박스에 '꽝'이 적힌 종이가 5장 있고, '선물'이 적힌 종이가 2장 있다. 3장을 뽑을 경우 다음 경우의 수 구하기

7C3 = 7! / 3!(7-3)! = 7! / (3! x 4!) = (7 x 6 x 5 x 4 x 3 x 2 x 1) / (3 x 2 x 1)(4 x 3 x 2 x 1) = (7 x 6 x 5) / (3 x 2 x 1) = 35

1) 꽝: 3, 선물: 0

5C3 = 5! / 3!(5-3)! = 5! / (3! x 2!) = 5 x 4 / 2! = 10

꽝: 3, 선물: 0의 확률: 10/35

2) 꽝: 2, 선물: 1

5C2 x 2C1 = (5! / 2!(5-2)!) x (2! / 1) = (5! / (2! x 3!)) x 2! = (5 x 4 / 2!) x 2! = 10 x 2 = 20

꽝: 2, 선물: 1의 확률: 20/35

3) 꽝: 1, 선물: 2

5C1 x 2C2 = (5! / (5-1)!) x (2! / (2!(2-2)!)) = (5! / 4!) x (2! / 2!) = 5

꽝: 1, 선물: 2의 확률: 5/35

1.2 Python을 이용한 확률

Example 1: 박스에 '꽝'이 적힌 종이가 4장 있고, '선물'이 적힌 종이가 3장 있을 때, Python을 이용해서 '꽝' 2장과 '선물' 1장을 뽑는 확률(%) 출력하기

def proFun():
    numN = int(input('numN 입력: '))
    numR = int(input('numR 입력: '))

    resultP = 1
    resultR = 1
    resultC = 1

    for n in range(numN, (numN - numR), -1):
        resultP = resultP * n
        print('resultP: {}'.format(resultP))

    for n in range(numR, 0, -1):
        resultR = resultR * n
        print('resultR: {}'.format(resultR))

    resultC = int(resultP / resultR)
    print('resultC: {}'.format(resultC))

    return resultC

sample = proFun()
print('sample: {}'.format(sample))

event1 = proFun()
print('event1: {}'.format(event1))

event2 = proFun()
print('event2: {}'.format(event2))

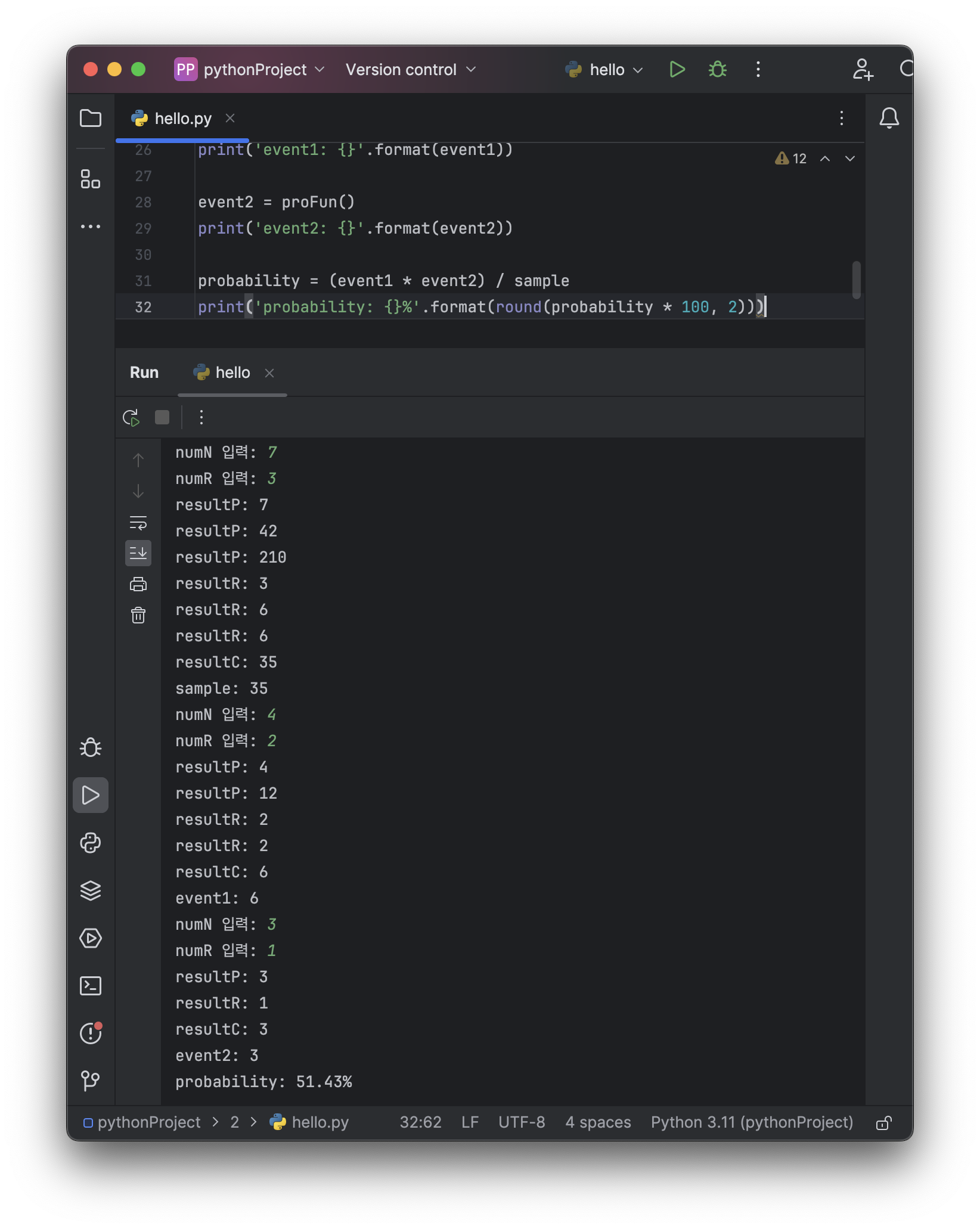
probability = (event1 * event2) / sample
print('probability: {}%'.format(round(probability * 100, 2)))