지난 글에서는 Sigmoid 에 대해서 살펴보았었다.

Sigmoid는 로짓을 확률로 바꿔주는 함수!

로 바꿔주면 수축, 팽창, 이동 을 표현할 수 있다고도 했었다.

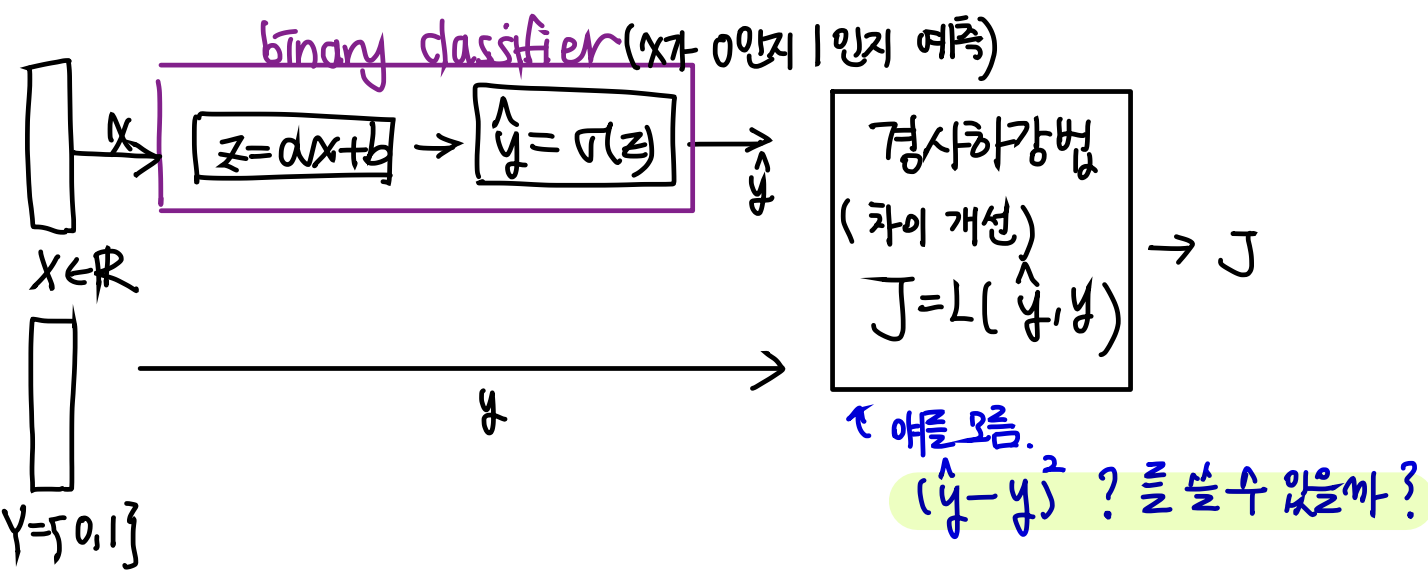
지난 글에서 배웠던 내용이다.
저 마지막에 Loss function 부분에서 $(\hat{y}-y)^2$를 쓸 수 있을까?

쓸 수 없는 이유는,
그 전이 binary classifier이기 때문에 출력값이 0,1 뿐이라 $(\hat{y}-y)^2$와 같이 쓰면 안된다.

따라서 loss function을 재설계 해야한다!

새로운 Loss Function의 설계가 필요하다.

오늘은 그에 대해 알아보자

Binary Cross Entropy

: Sigmoid의 출력과 0,1 사이의 값을 갖는 레이블 사이의 차이를 개선할 수 있는 loss function

이 Loss function의 요구사항을 살펴보자.

• $\hat{y} \in (0,\; 1),\; y \in \{0,\; 1\}$
• 아래로 볼록(convex)
• 미분 가능한 함수
• 차이가 작으면 $J \approx 0$, 차이가 크면 $J \rightarrow \infty$

즉 설계할 방향은

• $\hat{y} \approx 0$, $y=1$ $\Longrightarrow$ $J \rightarrow \infty$
• $\hat{y} \approx 0$, $y=0$ $\Longrightarrow$ $J \rightarrow 0$
• $\hat{y} \approx 1$, $y=1$ $\Longrightarrow$ $J \rightarrow 0$
• $\hat{y} \approx 1$, $y=0$ $\Longrightarrow$ $J \rightarrow \infty$

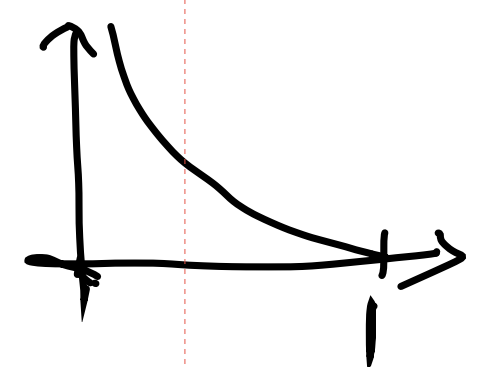
이해가 안가면 그림으로 살펴보자.

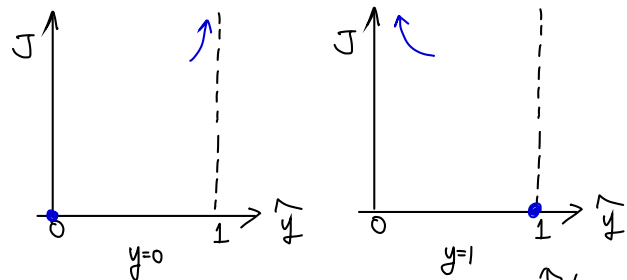
$\hat{y}$은 파란 점을 보면 된다.
해당 점을 지나면서 파란 화살표 방향대로 이동하는 함수는 어떤 것들이 있을까?

• 첫번째 아이디어 : 지수함수
  

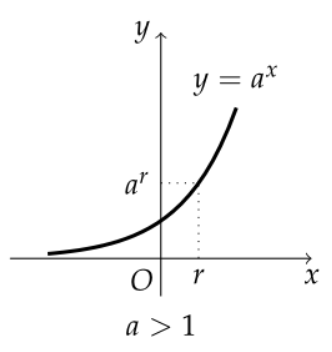
  안된다... 실수 전체가 정의역이기 때문! pass!

• 두 번째 아이디어 : tanh(x)함수
  

  역시 안된다. 출력값이 (-1, 1)이기 때문, pass!

• 세 번쨰 아이디어 : log 함수
  

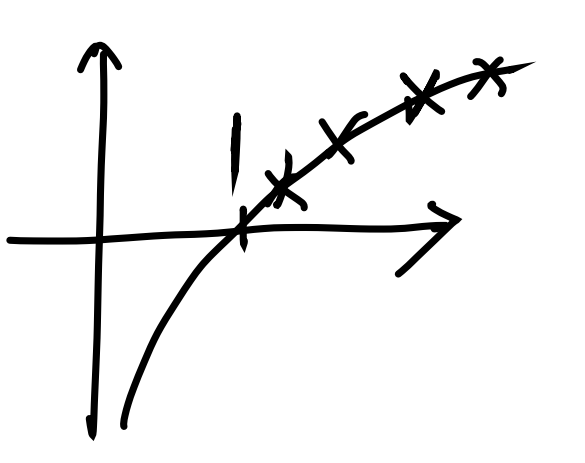
  애매하지만, $0<x<1$인 부분만 살리면 가능할 것 같다!

저 부분만 살리기 위해서 우리는 로그함수에 x축 대칭($y:=-y$)이 필요하다.

식을 다시 써보면

가 된다. 그래프는 아까 우리가 원했던 대로

이렇게 나온다. 위 함수를 아까 그렸던 두 그래프중 $y=1$인 그래프에 제대로 그려보면,

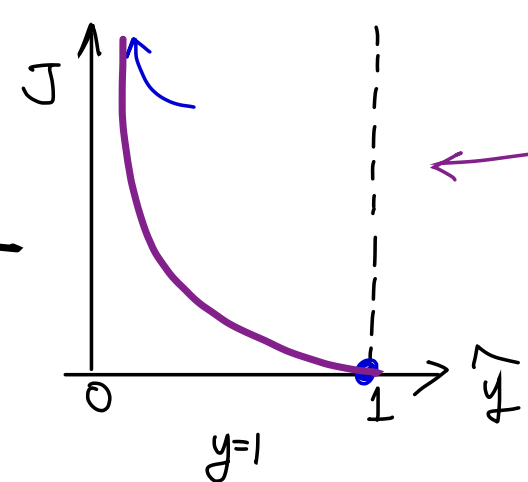
정확히 우리가 원하는 그래프가 되었다. 그렇다면 $y=0$의 그래프는 어떻게 그릴까?

처음에 생각했던 방법은, y축에 대칭하고 x축으로 평행이동이었지만 생각보다 간단한 방법이 있었다. 바로,
$x=0.5$축에 대칭하면 된다!
즉, $x:=1-x$를 대입하면 된다.

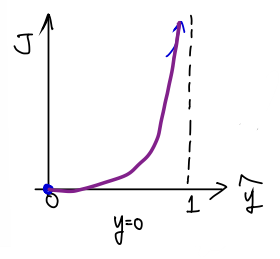
위 그래프는 아래 수식을 만족한다

그럼 방금 $y=0$일때와 $y=1$일 때 수식을 전체적으로 정리해보자.

하지만 우리가 어디든 적용할 때마다 이렇게 두 상황으로 나눠서 사용할 수 없으니(if문을 사용하게 되면 복잡해진다) , 이 두 함수를 합치기로 한다.

두 항으로 나누어서 해석하면 이해할 수 있을 것이다!
또한 이 loss함수를 그래프로 나타내면

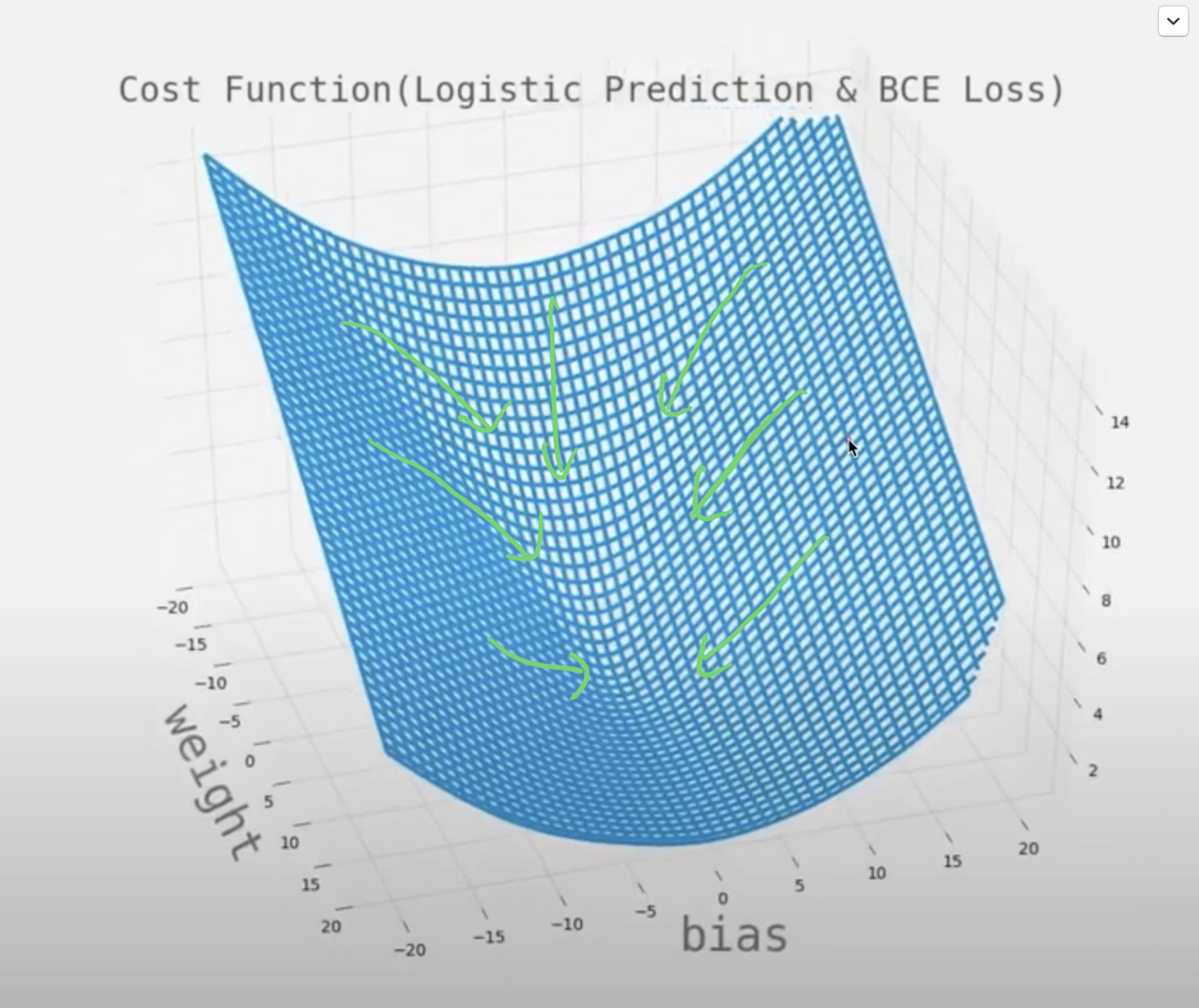
위와 같이 나타나서 우리가 원했던 convex함 조건에 부합한다.

사진이 여러개 들어가서 렉이 먹으니 다음 글에서 bce를 사용한 Loss function에 대해 더 자세히 알아보자.