저번 글에서 언급한 Multilayer Perceptrons에 대해서

마지막 레이어에서 affine function만 통과하면, 출력은 5개 출력인데 -무한에서 +무한까지 가능하다.
만약 마지막에 Sigmoid를 넣으면 독립적인 값이 나와서 합이 1이 나오지 않는다.
따라서 마지막 레이어의 출력은 5개의 Logit으로 생각한다.
Logit 하나를 확률로 바꿔주는 것이 Sigmoid이고
이번에는 Logit벡터를 확률로 바꿔주는것이 Softmax이다.

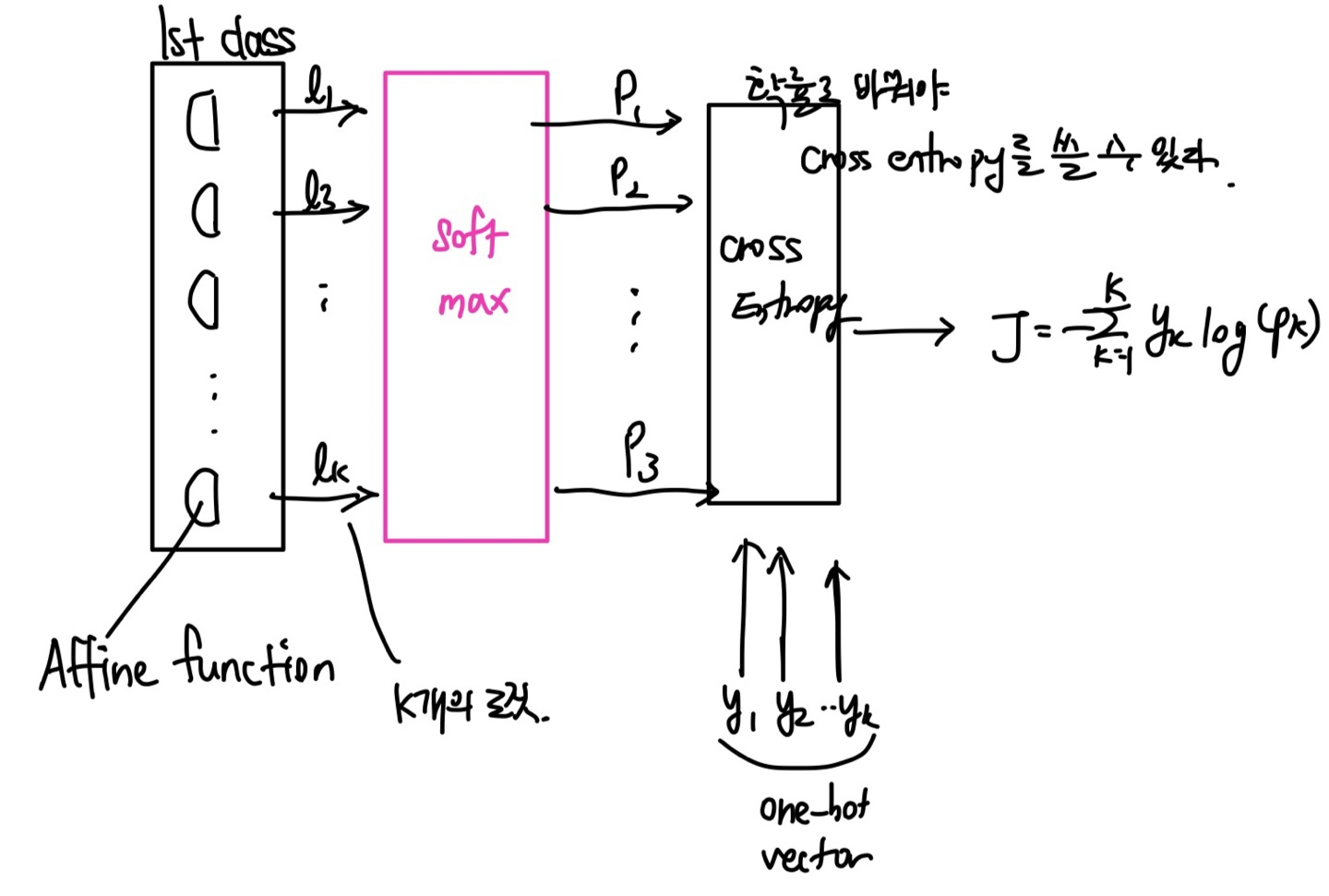
activation을 거치지 않고 나오면 -무한 +무한 사이값이 나온다. 이 값을 확률로 바꿔주는 것.
만약 activation을 거치면 로짓의 특성과 달라지기 때문에 로짓으로 해석할 수 없게 된다.
따라서 activation을 뺀 결과를 softmax에 넣어 확률로 만들고, 그 결과를 cross entropy에 넣는다.

Review

• 뉴런 네트워크의 마지막 레이어에 activation을 달아주지 않는다.
• 출력값인 로짓을 soft max에 입력, 그리고 probability vector을 출력한다.
• probability vector 와 실제값인 label을 cross entropy에 넣어준다.

  분류 문제에서만 마지막에 softmax!

Softmax 공식

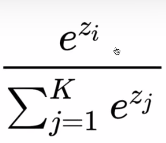
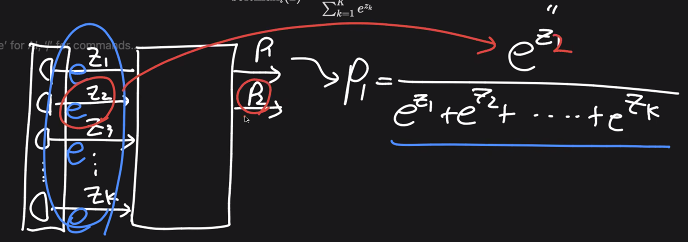
처음에 반쪽짜리 affine function에서 z를 받고, 여기에 softmax 첫번째 값을 넣으면

이런 값이 나온다.
즉 이 값이 첫번째 probability = p_1값

즉, affine function 결과값 모두에 e를 씌워주고 그 합계로 나눈다.는 뜻이다.

위 내용을 코드로 작성해보자.

import torch

logit_vector = torch.rand(10)
print(logit_vector)

prob_vector = torch.exp(logit_vector)/torch.sum(torch.exp(logit_vector))
print(prob_vector)
print(prob_vector.sum())

처음 출력된 값은 affine function의 출력값이고
두번째로 출력된 값은 e를 씌우고 전체 합으로 나눈 p_k를 구하는 과정이다.

마지막으로 위 수식처럼 출력된 것으로 p를 다 더하면 1이 나옴을 확인할 수 있다.

전체 코드

import torch.nn as nn

BATCH_SIZE = 4
N_CLASSES = 7

preds_logits = torch.rand(BATCH_SIZE, N_CLASSES)
print(preds_logits)

pred_probs = torch.exp(preds_logits)/torch.exp(preds_logits).sum(axis=1).reshape(-1,1)
print(pred_probs)
print(pred_probs.sum(axis = 1))

첫번째 출력이 affine function을 통과한 값,
두번째 출력이 softmax를 통과한 값이다.
마지막 출력은 axis=1에서의 합이 1임을 보여준다.