따로 실습이 없다
합성곱 신경망을 구성하는 기본 개념과 동작 원리를 배우고 간단한 합성곱, 풀링 계산방법을 익힌다.
.
.
.
도장!
1. 합성곱
합성곱(convolution)은 입력데이터에 도장을 찍듯이 유용한 특성만 드러나게 하는 것으로 비유할 수 있다.
- 1차원에서의 합성곱
w1~w10과 절편 b를 랜덤하게 초기화한 다음, 에포크를 반복하면서 경사하강법 알고리즘을 사용해 손실이 낮아지도록 최적의 가중치와 절편을 찾아간다
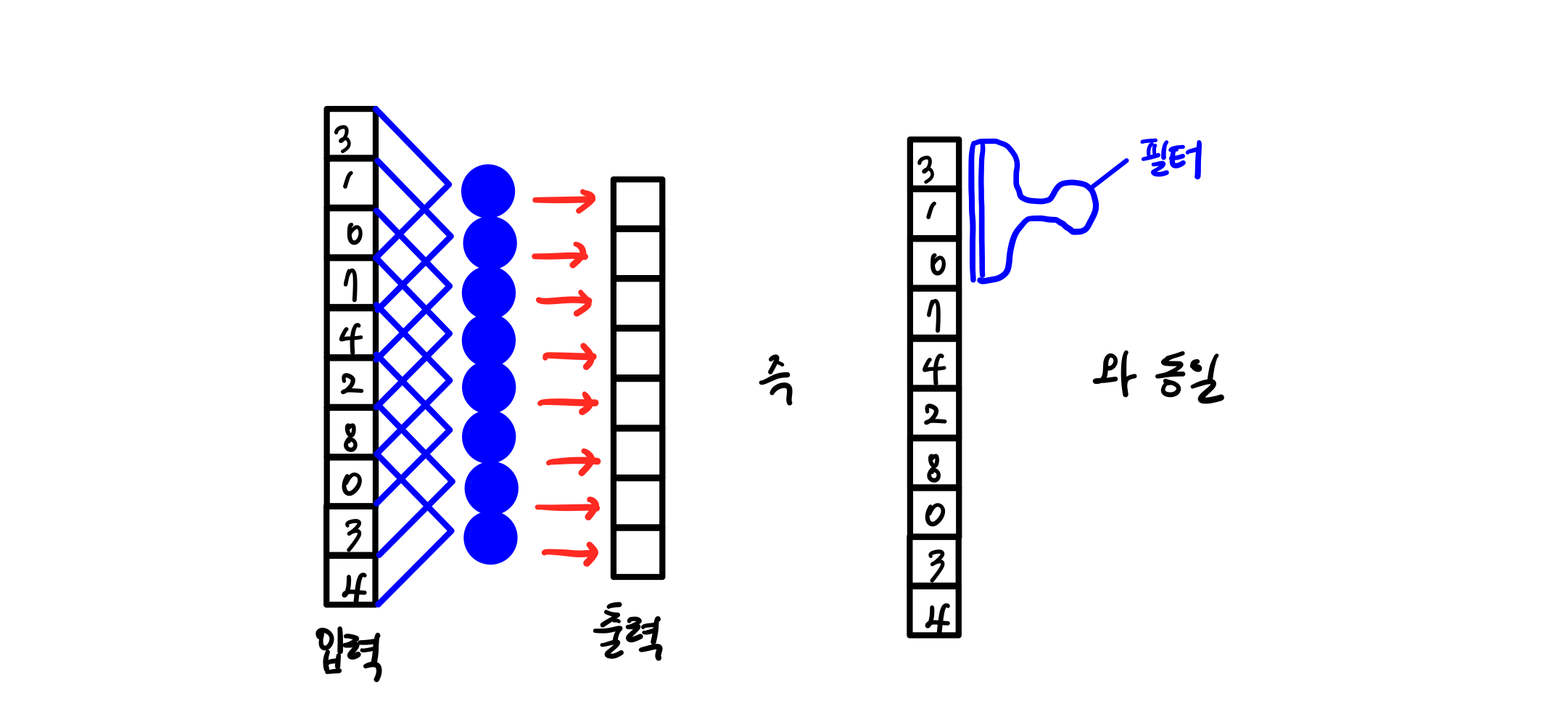
일부에만 가중치를 곱한다
뉴런이 입력 위를 이동하면서 출력을 만들기 때문에 합성곱 신경망에서는 뉴런을 필터라고 부른다.
필터 : 뉴런 개수
커널 : 입력에 곱해지는 가중치
- 2차원에서의 합성곱
입력이 2차원 배열이면 필터(도장!)도 2차원이어야 합니다.
입력의 크기가 (4,4), 필터의 커널 크기가 (3,3)이라 가정할 때 입력의 9개 원소와 커널의 9개 가중치를 곱한 후 1개의 출력을 만든다. 따라서, 총 4개의 출력을 만든다.
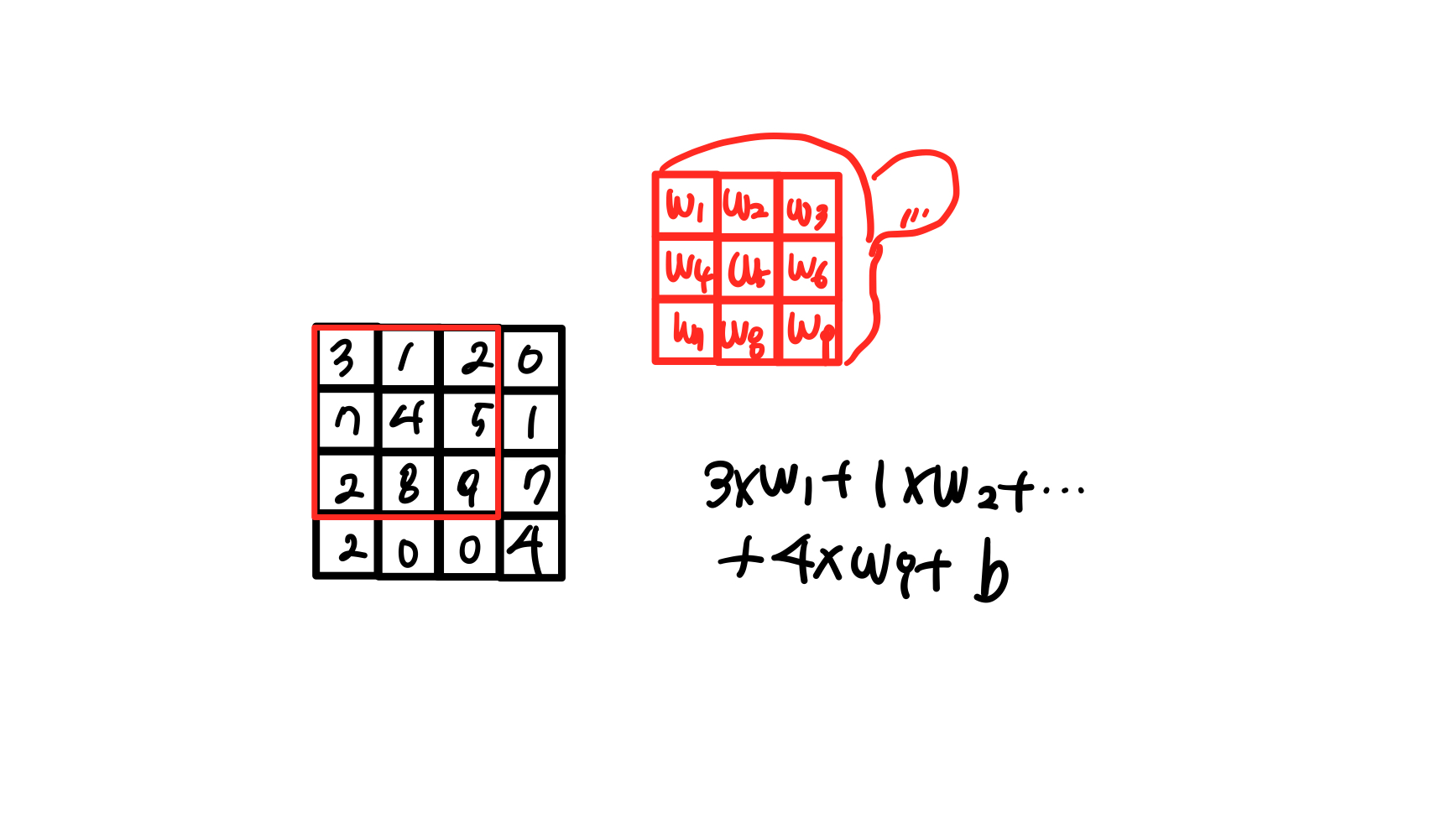
합성곱 계산을 통해 얻은 출력을 특별히 특성 맵(feature map)이라고 부른다.
특성맵이 3차원 배열 일 경우
합성곱 층에서 여러개의 필터를 사용할 때, 만들어진 특성맵은 순서대로 차곡 차곡 쌓인다. 2차원 크기의 특정 맵을 쌓으면 3차원 배열이 됩니다.
합성곱 신경망이 2차원 구조를 그대로 사용하기 때문에 이미지 처리 분야에서 뛰어난 성능을 발휘한다.
2. keras 합성곱 층
Conv2D클래스
keras.layers.Conv2d(10, kernel_size=(3,3), activation='relu')1번째 매개변수(10)은 필터의 개수, kernel_size는 필터에 적용할 커널의 크기, 마지막으로 합성곱 층에도 활성화 함수를 적용한다.
- 패딩과 스트라이드
출력의 크기를 변경하고 싶을 경우 → 마치 더 큰 입력에 합성곱하는 척을 해야됨
(1) 패딩
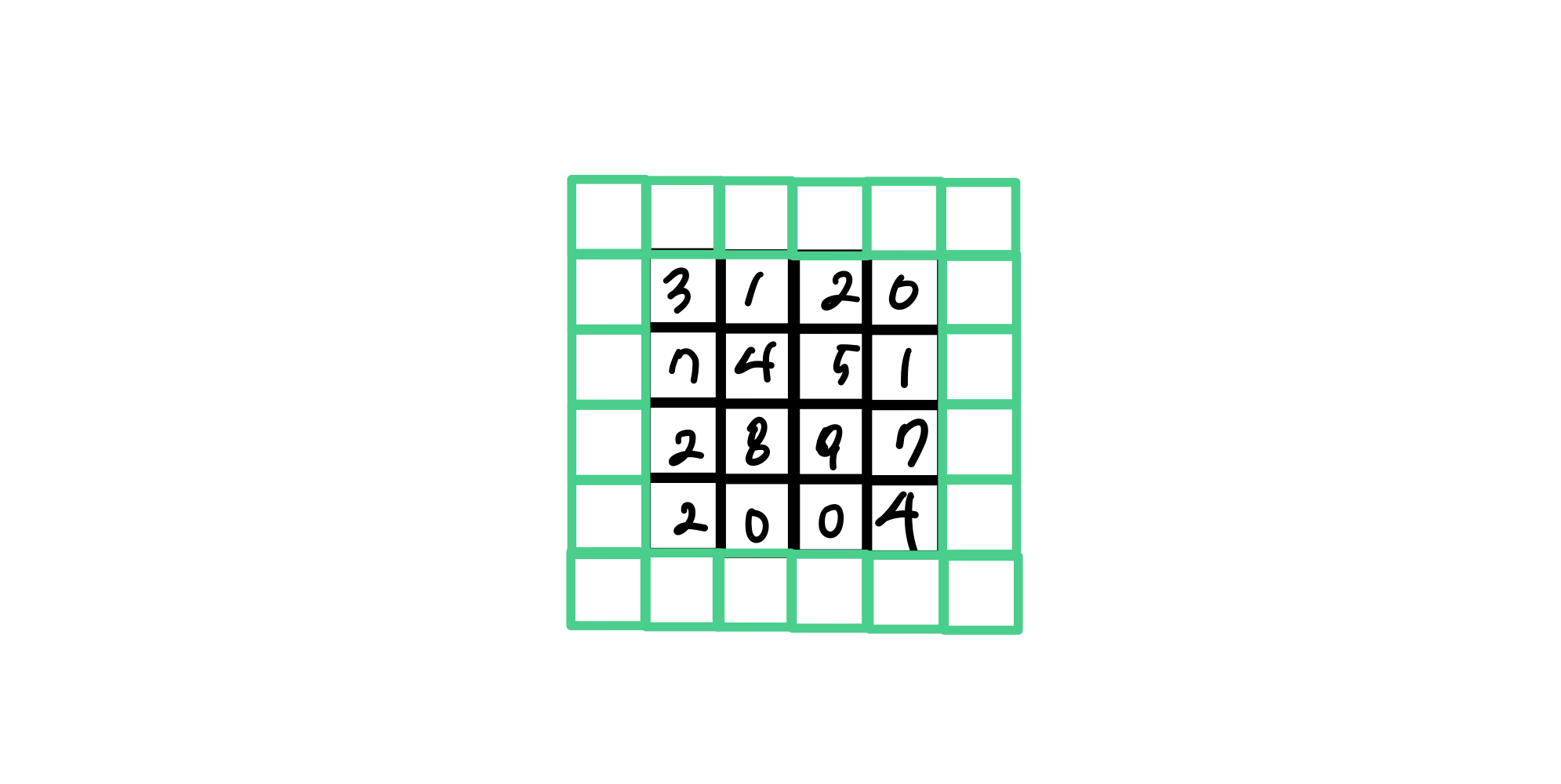
이렇게 입력 배열 주위를 가상의 원소로 채우는 것을 패딩이라고 한다. 실제 입력값 이외의 패딩은 0으로 채우며, 도장을 찍을 횟수를 늘려주는 역할밖에 안하기 때문에 계산에 영향을 미치지는 않는다.
- 입력 주위에 0으로 패딩 하는 것을 세임 패딩이라고 부른다.
- 패딩 없이 순수한 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 경우는 밸리드 패딩이라고 한다. (특성맵의 크기가 줄어들 수 밖에 없다.)
합성곱 신경망에서는 세임 패딩이 많이 사용된다. (입력과 특성 맵의 크기를 동일하게 만드는 경우가 대부분이다)
또한, 적절한 패딩은 이미지의 주변에 있는 정보를 잃어버리지 않도록 도와준다. 아래 입력을 이미지라고 생각하면 모서리에 있는 중요한 정보가 특성 맵으로 잘 전달되지 않을 가능성이 높다. 반면 가운데에 있는 정보는 두드러지게 표현된다.
1픽셀씩 패딩을 하면 이 차이는 크게 줄어든다.
(2) 스트라이드
도장 이동의 크기를 스트라이드라고 한다. 기본으로 스트라이드 1이지만 1보다 큰 스트라이드를 상ㅇ하는 경우는 드물다.(strides 매개변수는 잘 사용하지 않는다.)
keras.layers.Conv2D(10, kernel_size=(3, 3), activation='relu', padding= 'same', strides=1)- 풀링
풀링은 합성곱 층에서 만든 특성맵의 가로세로 크기를 줄이는역할을 수행한다. (*특성맵의 개수는 줄이지 않는다)
특성 맵에 커널(가중치)없는 필터를 적용하는 것과 동일하다.
풀링에는 가중치가 없는 대신, 도장을 찍은 영역에서 가장 큰 값(최대 풀링)을 고르거나 평균값(평균 풀링)을 계산한다.
풀링에서는 위에서 배운 필터와 달리 겹치지 않고 이동한다는 것을 주의해야 한다. 풀링에는 가중치가 없고 풀링 크기와 스트라이드가 같다.
keras.layers.MaxPooling2D(2, strides =2, padding='valid')평균 풀링보다는 최대 풀링을 많이 사용한다. 평균 풀링은 특성 맵에 있는 중요한 정보를 (평균하여) 희석시킬 수 있기 때문이다.
3. 합성곱 신경망의 전체 구조
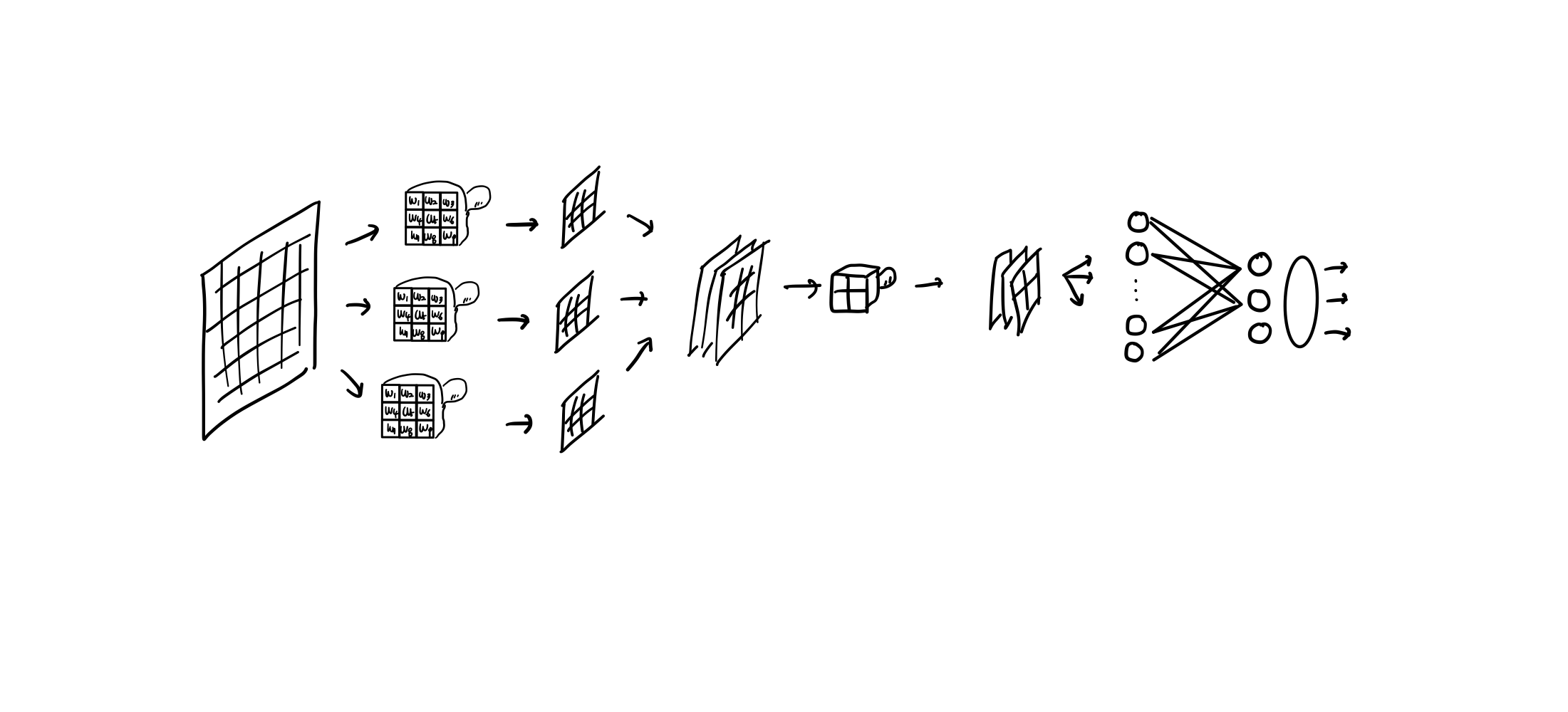
입력에 필터가 패딩에 따라 적용되고 (합성곱 층에서도 활성화 함수를 적용한다) 출력된 특성맵은 풀링층에 의해 크기가 줄어든다. 풀링을 거친 특성맵은 밀집층인 출력층에 전달되려면 3차원 배열이 1차원 배열로 펼쳐져야 한다.(Flatten 클래스) 펼쳐진 1차원 배열은 연산을 거쳐 출력층의 클래스를 분류하는 다중분류 문제로 전달된다.
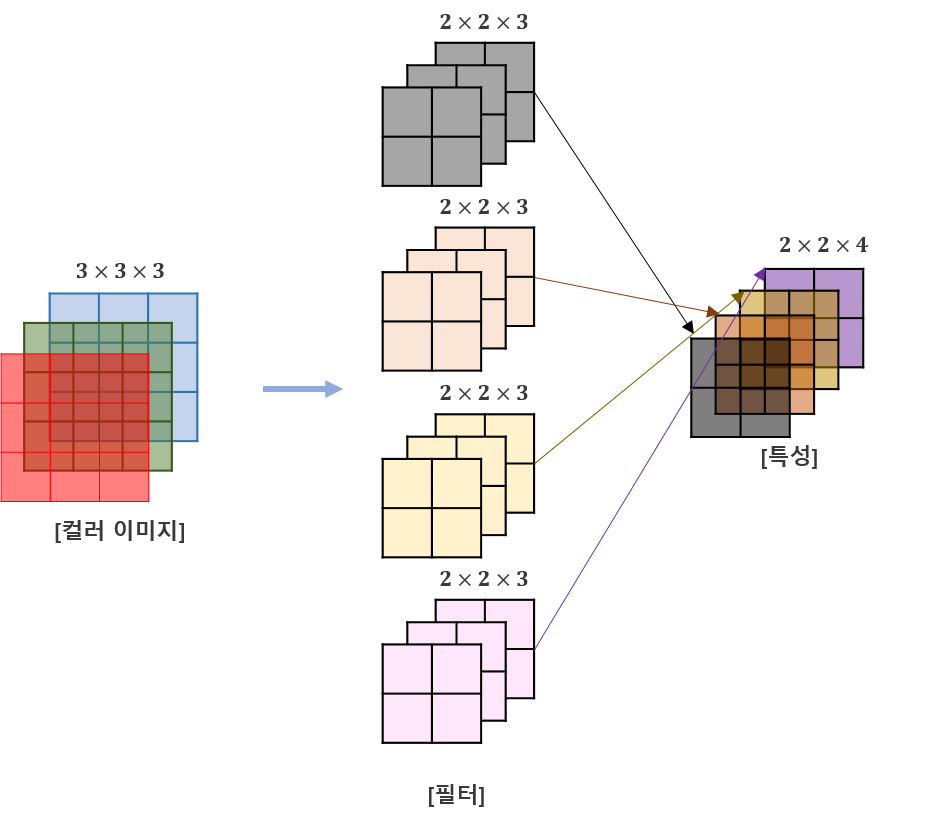
컬러이미지(3차원)을 사용한 합성곱
컬러 이미지는 RGB 채널로 구성되어 있기 때문에 컴퓨터는 이를 3차원 배열로 표시한다.
입력의 크기가 (4, 4, 3)일 때 필터(도장)도 (3, 3, 3)으로 깊이가 필요하다. (커널 배열의 깊이는 항상 입력의 깊이와 동일하다)
필터의 차원이 몇개인지 상관없이 항상 출력은 하나의 값이다. (특성맵에 있는 한 원소가 채워진다)
정리하며
합성곱 신경망은 너비와 높이는 점점 줄어들고 깊이는 점점 깊어지는 것이 특징이다.
합성곱 신경망에서 필터는 이미지에 있는 어떤 특징을 찾는다고 생각할 수 있다. 처음에는 간단한 기본적인 특징(직선, 곡선 등)을 찾고 층이 깊어질 수록 다양하고 구체적인 특징을 감지할 수 있도록 필터의 개수를 늘인다. 또 어떤 특징이 이미지의 어느 위치에 놓이더라도 쉽게 감지할 수 있도록 너비와 높이 차원을 점점 줄여간다.