💠 AIchemist 8th Session | 차원 축소

01. 차원 축소(Dimension Reduction) 개요

차원 축소
매우 많은 피처로 구성된 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것

(기존의 문제점)
차원이 클수록 데이터 포인트 간 거리가 기하급수적으로 멀어져 희소한 데이터 구조를 가지게 됨 -> 예측 신뢰도가 떨어짐
개별 피처 간의 상관관계가 높을 가능성이 큼 (선형회귀 모델에서 다중공산성 문제 발생)

• 피처 수를 줄이면 더 직관적으로 데이터를 해석할 수 있음
• 시각적으로 데이터를 압축해서 표현 가능
• 학습에 필요한 처리 능력도 줄일 수 있음

1. 피처 선택
   특정 피처에 종속성이 강한 불필요한 피처는 아예 제거하고 데이터 특징을 잘 나타내는 주요 피처만 선택
2. 피처 추출
   기존 피처를 저차원의 중요 피철로 압축해서 추출하는 것
   또 다른 공간으로 매핑해 추출 -> 함축적인 요약 특성으로 추출

차원 축소를 통해 좀 더 데이터를 잘 설명할 수있는 잠재적인 요소를 추출

02. PCA(Principal Component Analysis)

PCA 개요

여러 변수 간에 존재하는 상관 관계를 이용해 이를 대표하는 주성분을 추출해 차원을 축소
주성분 (가장 높은 분산을 가지는 데이터 축을 찾아 이 축으로 차원을 축소)

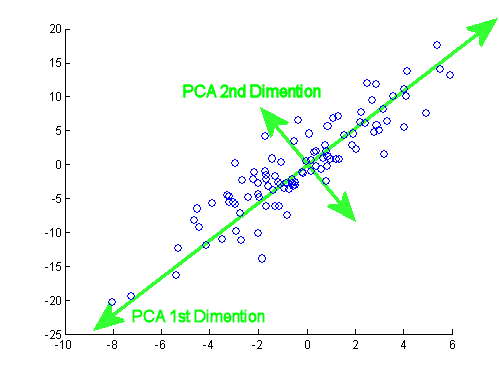
데이터 변동성이 가장 큰 방향으로 축을 생성하고, 새롭게 생성된 축으로 데이터를 투영

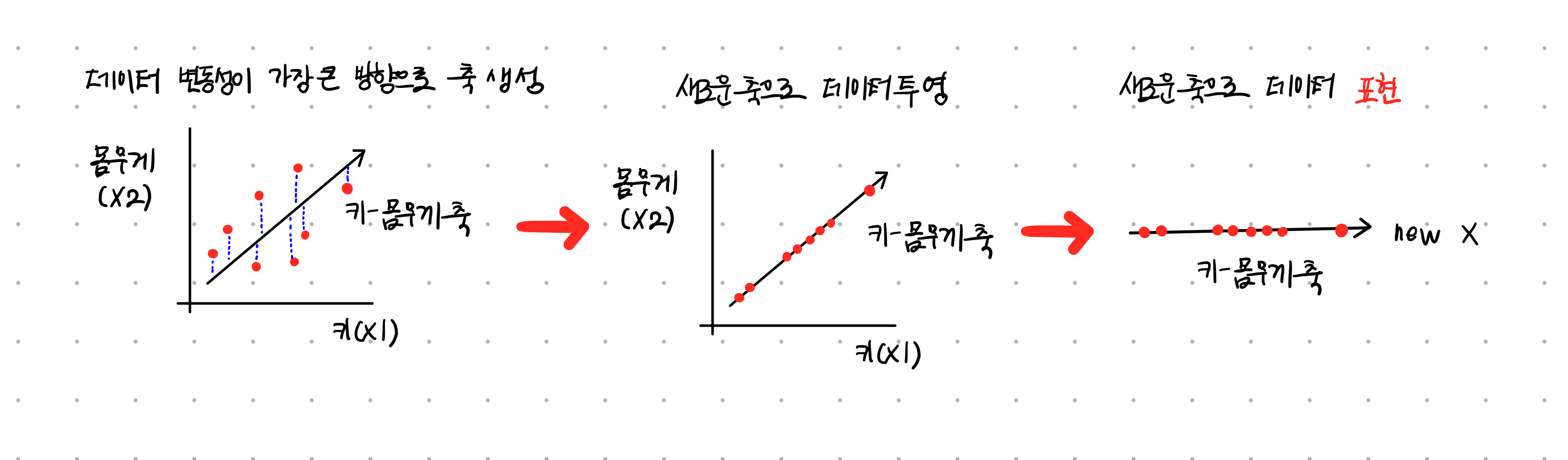
벡터 축의 개수만큼의 차원으로 원본 데이터 차원 축소됨

고유 벡터가 PCA의 주성분 벡터로서 입력 데이터의 분산이 큰 방향을 나타냄
고윳값은 입력 데이터의 분산을 나타냄

1. 선형 변환

특정 벡터를 하나의 공간에서 다른 공간으로 투영
공분산은 두 변순 간의 변동(분산)을 의미

2. 고유 벡터

행렬 A룰 곱하더라도 방향이 변하지 않고 그 크기만 변하는 벡터를 지칭

Ax = ax (a는 고윳값, x는 고유 벡터)

3. 공분산 행렬

정방행렬이자 대칭행렬

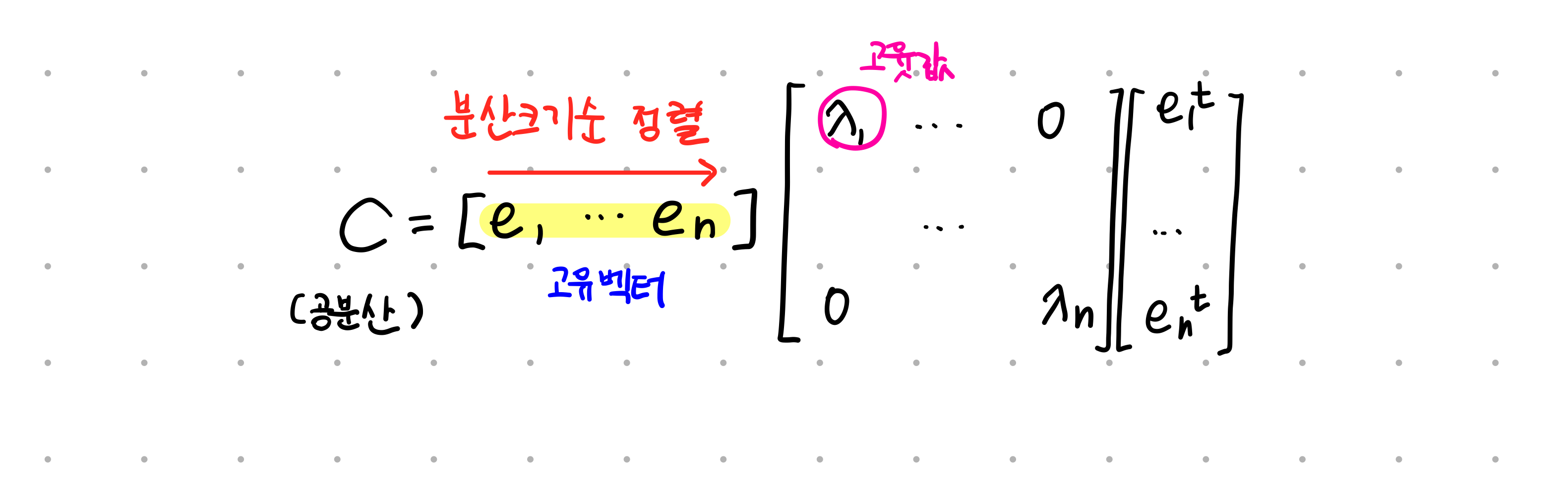
e1은 가장 분산이 큰 방향을 가진 고유벡터이며, e2는 e1에 수직이면서 다음으로 가장 분산이 큰 방향을 가진 고유벡터

PCA 위 식을 이용해 분해된 고유벡터를 구하고 찾은 고유벡터를 이용해 입력 데이터를 선형 변환하는 방식

1. 입력 데이터 세트의 공분산 행렬을 생성
2. 공분산 행렬의 고유벡터와 고유값을 계산
3. 고유값이 가장 큰 순으로 K개 만큼 고유벡터를 추출
4. 고유값이 가장 큰 순으로 추출된 고유벡터를 이용해 새롭게 입력데이터를 변환

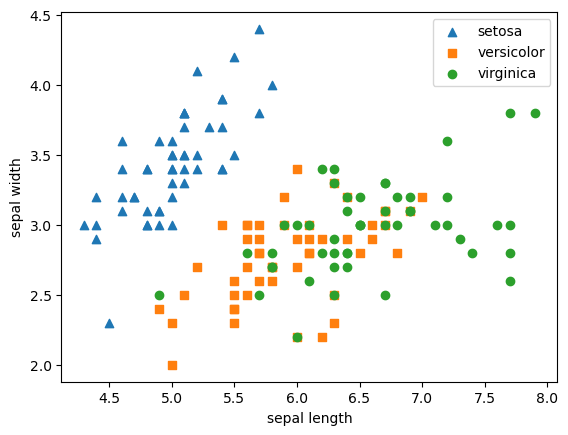
섞여서 분포하기 때문에 length/width로 품종 분류 어려움
-> 4개의 속성(sepal_length, sepal_width, petal_length, petal_width)을 2개의 PCA 속성으로 압축

1. 스케일링

여러 속성의 값을 연산해야 되므로 StandardScaler를 이용해 정규분포로 스케일링

from sklearn.preprocessing import StandardScaler

# Target 값을 제외한 모든 속성 값을 StandardScaler를 이용해 표준 정규 분포를 가지는 값들로 변환
iris_scaled= StandardScaler().fit_transform(irisDF.iloc[:, :-1])

2. PCA 훈련

from sklearn.decomposition import PCA 

pca = PCA(n_components=2)

# fit()과 transform()을 호출해 PCA 변환 데이터 반환
pca.fit(iris_scaled)
iris_pca = pca.transform(iris_scaled)
print(iris_pca.shape)

PCA가 분산을 고려 새로운 component(압축된 피처)를 생성

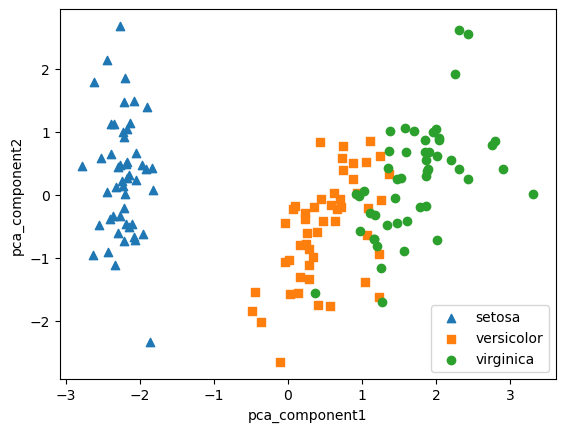
PCA 컴포넌트별로 차지하는 변동성 비율을 제공

print(pca.explained_variance_ratio_)

[Output]
[0.72962445 0.22850762]

pca_component_1이 전체 변동성의 약 72.9% 차지, pca_component_2가 약 22.8% 차지

Default of credit card client Data set

read_excel 에러 발생해서 csv로 변환
'default payment next month' 속성이 Target 값으로 '연체'일 경우 1, '정상 납부'일 경우 0
>> 타깃값을 분류 예측(연체인 경우/ 정상납부인 경우로 분류)

24개의 속성끼리 상관도가 매우 높음

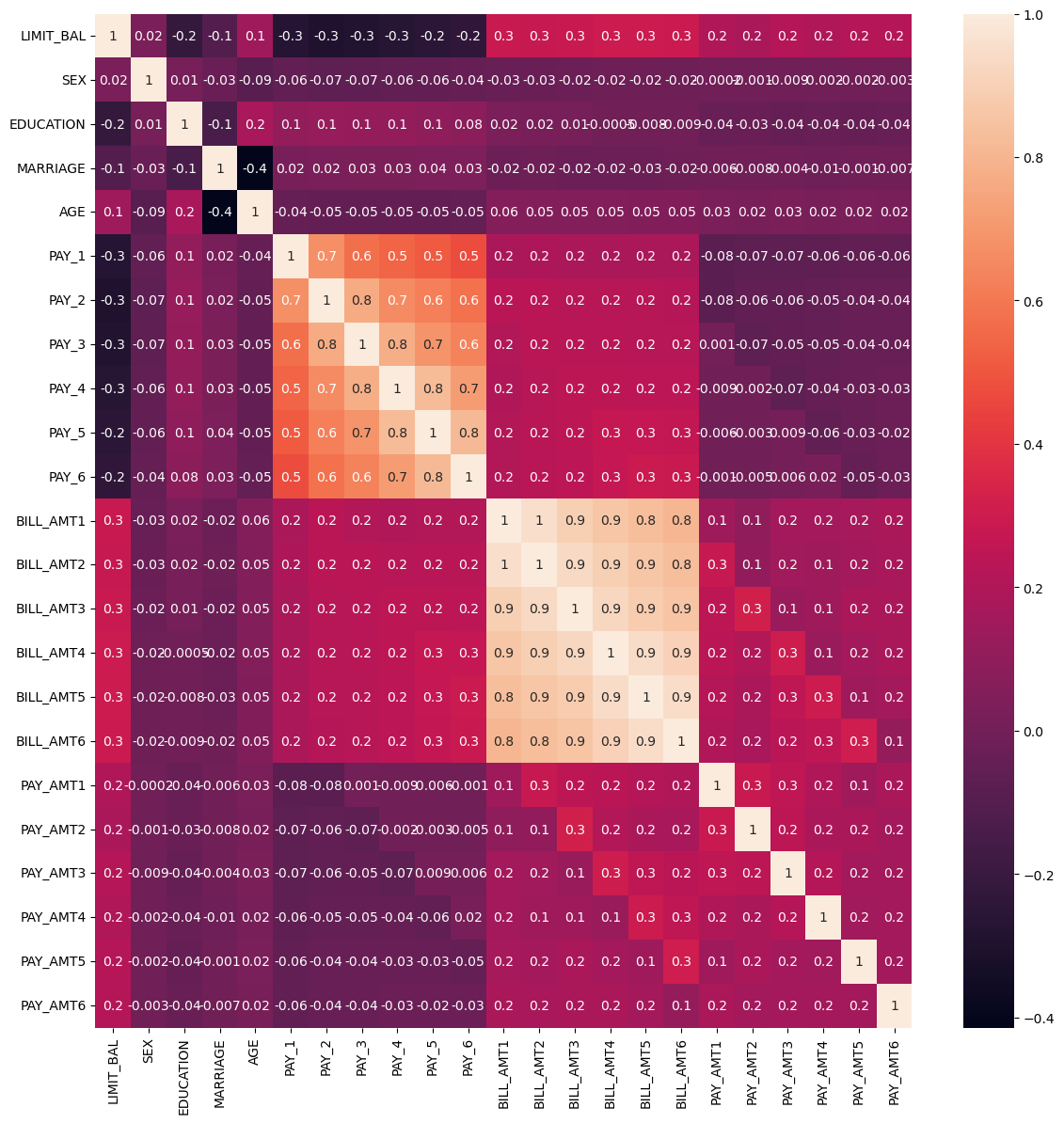
BILL_AMT1~BILL_AMT6 속성 끼리 상관도가 매우 높음
6개의 속성을 2개의 component로 PCA 변환

• scaling & PCA

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
​
#BILL_AMT1 ~ BILL_AMT6까지 6개의 속성명 가짐
cols_bill = ['BILL_AMT'+str(i) for i in range(1, 7)]
print('대상 속성명:', cols_bill)
​
#2개의 PCA 속성을 가진 PCA 객체 생성하고, explained_variance_ratio_ 계산을 위해 fit() 호출
scaler = StandardScaler()
df_cols_scaled = scaler.fit_transform(X_features[cols_bill])
pca = PCA(n_components = 2)
pca.fit(df_cols_scaled)
print('PCA Component 별 변동성:', pca.explained_variance_ratio_)

[Output]
대상 속성명: ['BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6']
PCA Component 별 변동성: [0.90555253 0.0509867 ]

2개의 PCA 컴포넌트 만으로 6개 속성 변동성을 약 95% 이상 설명할 수 있음.

최종 예측 결과는 원본과 비교해 1~2% 정도의 예측 성능 저하만 발생
PCA의 뛰어난 압축 능력을 보여줌

03. LDA(Linear Discriminant Analysis)

선형 판열 분석법, PCA와 유사하지만 지도학습의 분류에서 사용하기 쉽도록 개별 클래스를 분별할 수 있는 기준을 최대한 유지하면서 차원을 축소

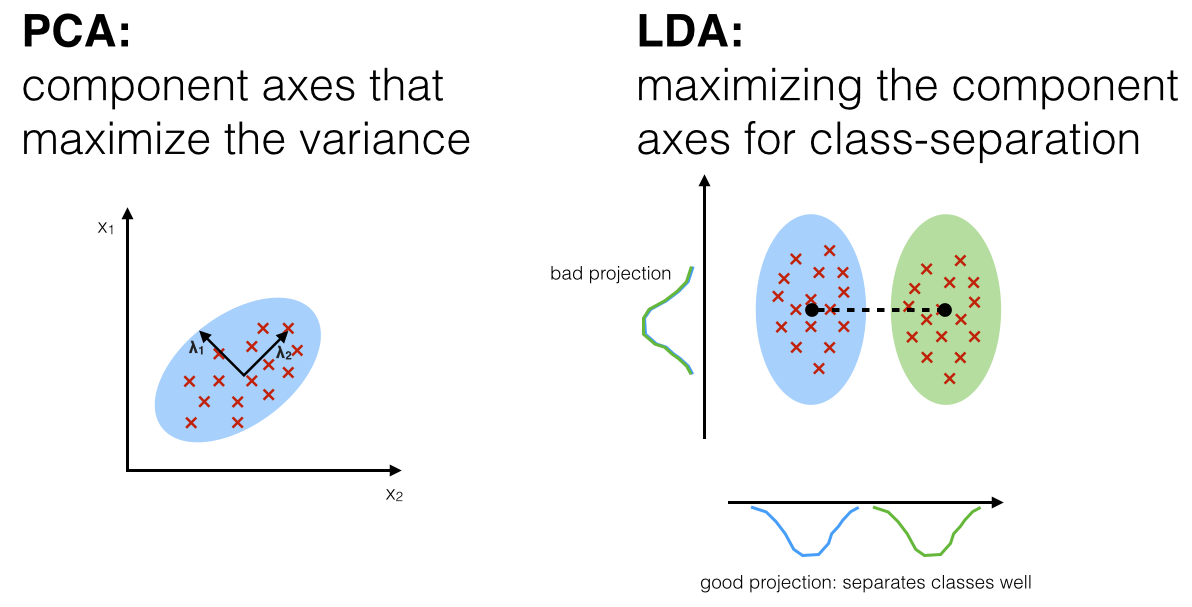
클래스 간 분산과 클래스 내부 분산 비율을 최대화하는 방식으로 차원을 축소
클래스 간 분산은 최대한 크게 가져가고, 클래스 내부의 분산은 최대한 작게 가져가는 방식

• 붓꽃 데이터 세트에 LDA 적용하기

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

iris = load_iris()
iris_scaled = StandardScaler().fit_transform(iris.data)
lda = LinearDiscriminantAnalysis(n_components=2)

lda.fit(iris_scaled, iris.target)
iris_lda = lda.transform(iris_scaled)
print(iris_lda.shape)

iris.target 클래스의 결정값이 변환 시에 필요

04. SVD(Singular Value Decomposition)

PCA와 유사한 행렬 기법을 적용하지만 SVD는 정방행렬 뿐만 아니라 행과 열의 크기가 다른 행렬에도 적용 가능

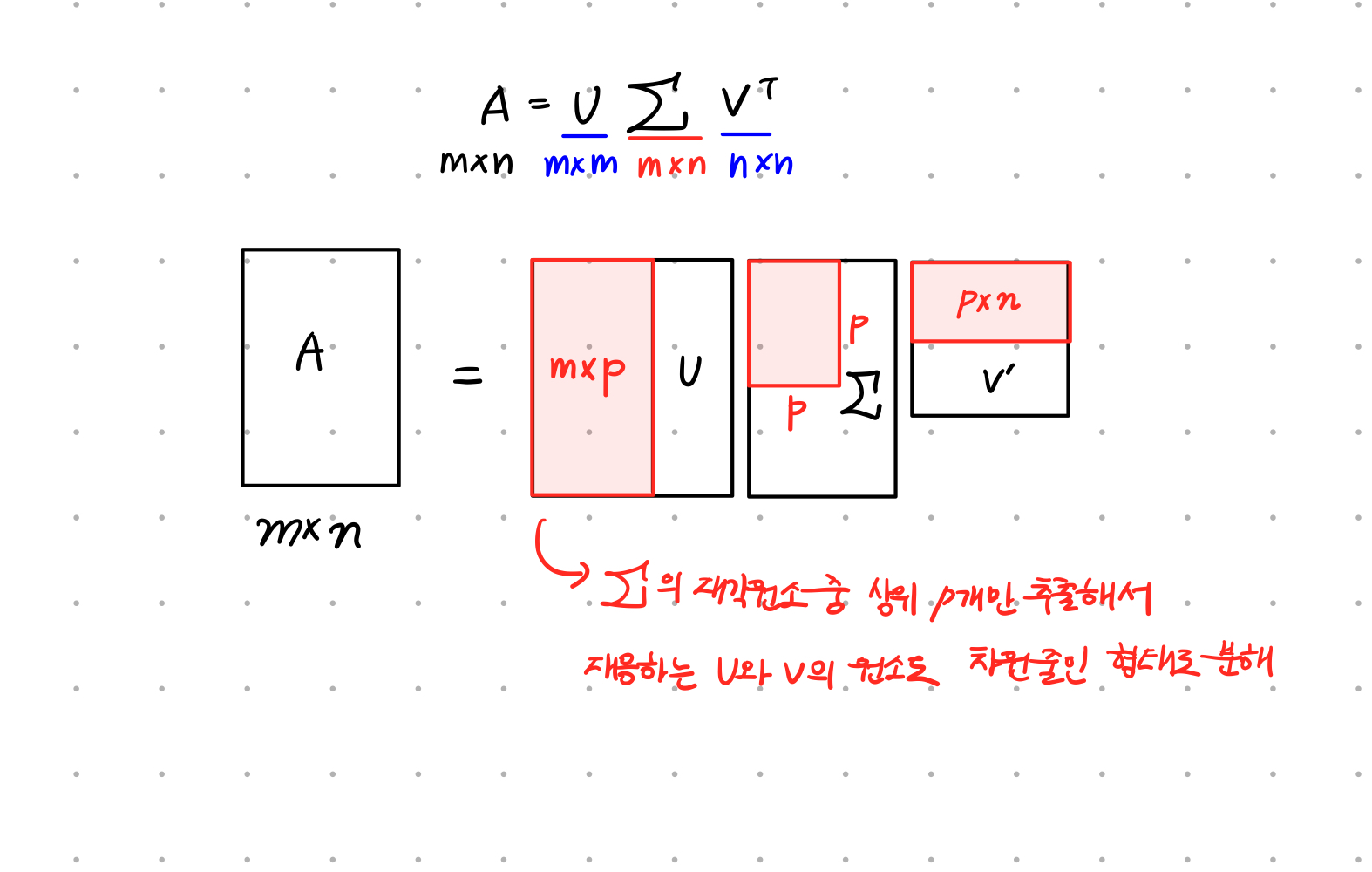
SVD(특이값 분해), U와 V에 속한 벡터는 특이 벡터

Trincated SVD
특이값 중 상위 일부 데이터만 추출해 분해하는 방식
인위적으로 더 작은 차원의 U, Sigma, V^T로 분해하기 때문에 원복 행렬을 정확하게 다시 원복할 수는 없음. 원래 차원의 차수에 가깝게 잘라낼수록 원복행렬에 더 까깝게 복원

Normal SVD로 분해해 분해된 행렬의 차원과 Sigma 행렬 내의 특이값을 확인 한뒤 다시 Truncated SVD로 분해된 행렬의 내적을 계산하여 다시 복원된 데이터와 원본 데이터는 차이 존재

• 사이킷런 TruncatedSVD 클래스를 이용한 변환

데이터 세트가 스케일링으로 데이터 중심이 동일해지면 사이킷런 SVD와 PCA는 동일한 변환을 수행.
PCA는 밀집 행렬에 대한 변환만 가능, SVD는 희소 행렬에 대한 변환도 가능.

05. NMF(Non-Negative Matrix Factorization)

(모든 원소 값이 모두 양수라는 게 보장되어야 함)
낮은 랭크를 통한 행렬 근사 방식의 변형

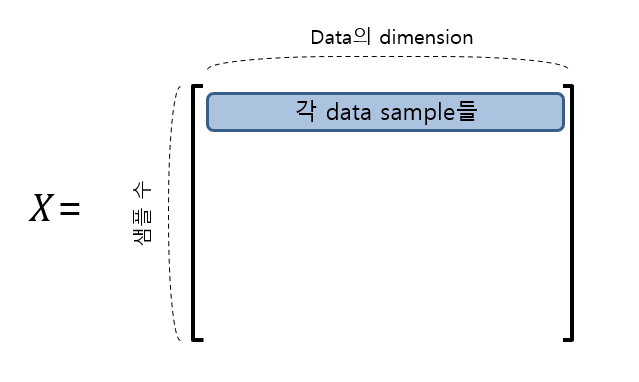
X = WH

W(원본 행렬과 행 크기는 동일하고 열 크기는 작은 행렬)와 H(원본 행렬의 행크 크기보다 작고 열 크기는 같은 행렬)로 행렬 분해

NMF 참고 자료

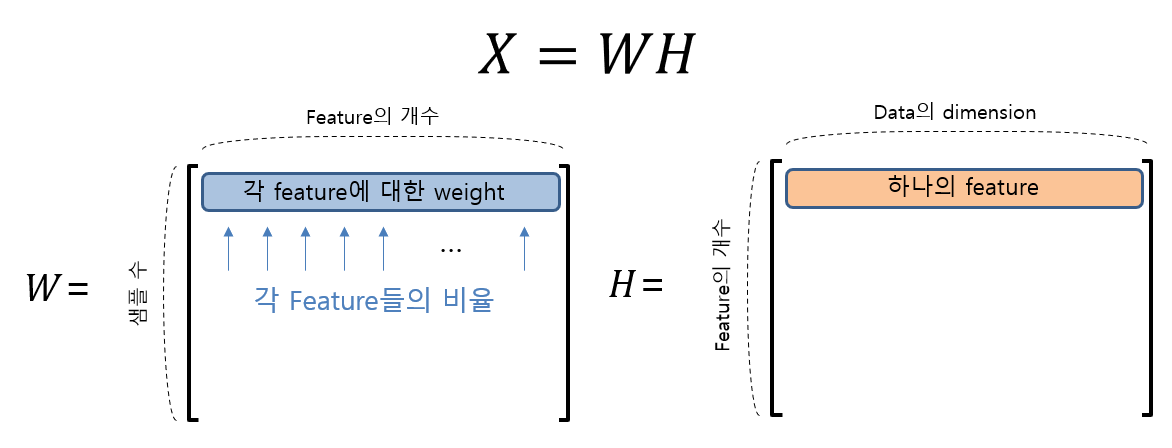
왜 NMF를 쓰는 것이 유용할 수 있을까?
non-negative 데이터는 non-negative feature로 설명하는 것이 좋다.
NMF가 유용한 이유 중 하나는 추출하게 되는 feature들이 모두 non-negative feature이기 때문이다.
...
그런데, 많은 경우에 사용되는 matrix factorization 방법들(가령, SVD)이나 차원 감소 방법(요인 분석, 주성분 분석, cluster 분석 등)에서는 획득할 수 있는 feature들이 음수이면 안된다던지 하는 제한사항같은 것은 없기 때문에 데이터의 특성인 non-negativity를 보존할 수 있다는 보장을 받을 수 없다는 한계점이 있다. -(Angelo's Math Notes)

• 사이킷런 NMF 클래스 이용해 2개의 컴포넌트로 변환

from sklearn.decomposition import NMF
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
%matplotlib inline

iris = load_iris()
iris_ftrs = iris.data
nmf = NMF(n_components=2)
nmf.fit(iris_ftrs)
iris_nmf = nmf.transform(iris_ftrs)
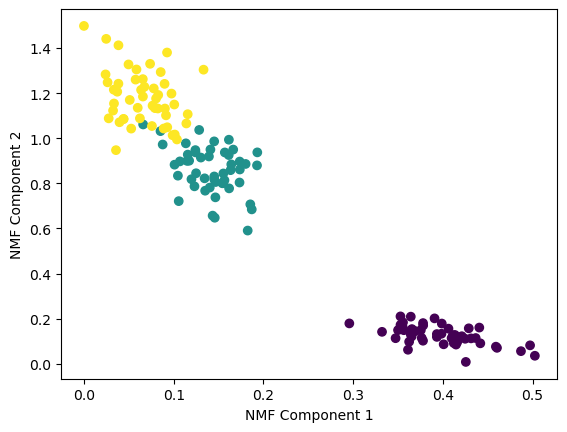
plt.scatter(x=iris_nmf[:,0], y= iris_nmf[:,1], c= iris.target)
plt.xlabel('NMF Component 1')
plt.ylabel('NMF Component 2')

plt.show()

이러한 행렬분해를 적용하면 원본행렬에서 잠재된 요소를 추출하기 때문에 토픽 모델링이나 추천 시스템에서 활발하게 사용됨.