백준 11403 - 경로 찾기

문제 파악

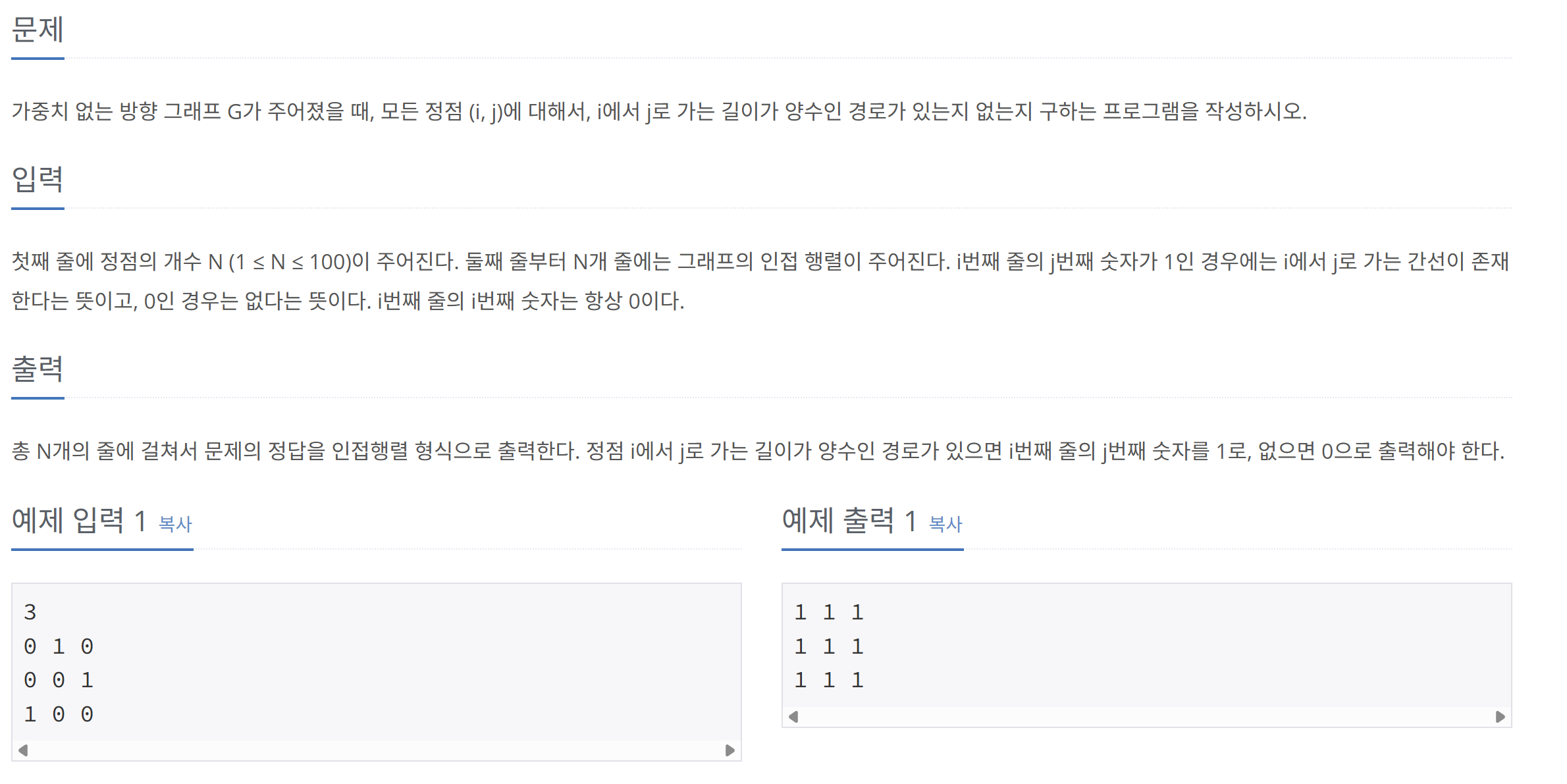
인접 행렬 형태의 그래프의 모든 정점(i, j)에 대해서 i에서 j로 가는 길이 있는지 구하는 문제
-> 모든 정점 쌍에 대해 경로가 있는지 여부를 구하는 것
모든 쌍 최단 경로

이 때 사용할 수 있는 알고리즘은 플로이드-워셜 알고리즘

• 다익스트라랑 다른 점 : 한 지점에서 다른 지점까지의 최단 경로를 구할 때는 다익스트라 선택(단계마다 최단 경로를 가지는 노드를 반복적으로 선택하며 최단 경로를 갱신하기 때문)
  하지만 플로이드-워셜은 2차원 테이블에 모든 지점에서 다른 모든 지점까지의 최단 경로를 기록하기 때문에 모든 정점 쌍의 경로를 구할 때 사용
  

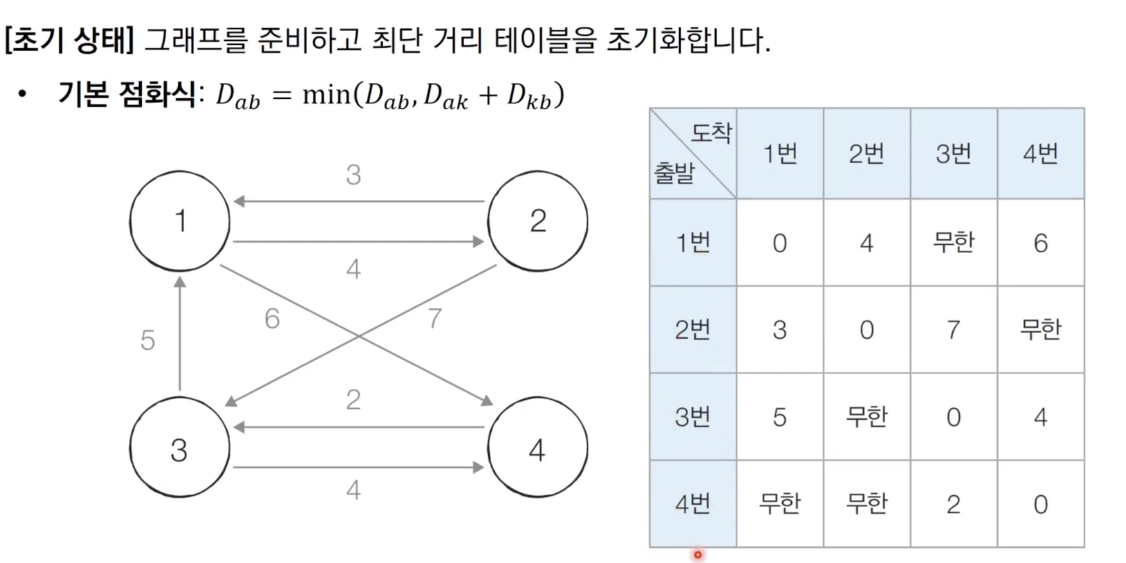
• 처음에 경유하지 않고 바로 갈 수 있는 노드(초기 비용)부터 채워넣기
  
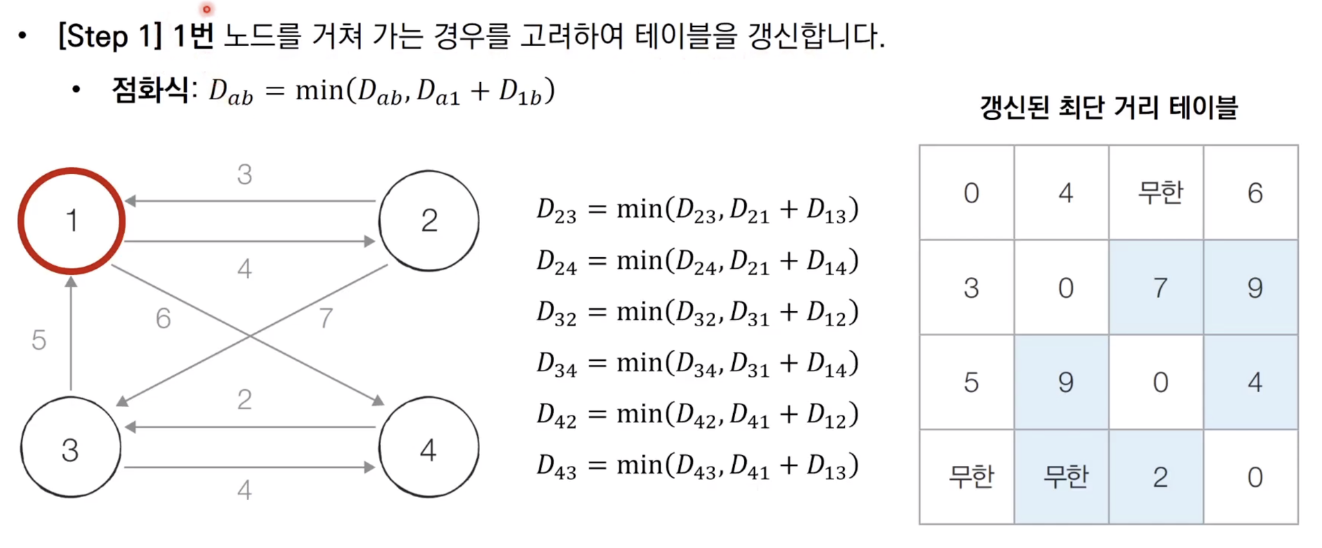
• 1번 노드를 경유해서 갈 수 있는 경우를 고려해 최단 거리 갱신
  -> 이런식으로 모든 노드를 다 경유해서 갈 수 있는 경우까지 계산한 후 최단 비용 계산

풀이

1. 정점 개수 N 입력 받기
2. 인접 행렬 (2차원 배열) 생성 및 초기화
3. 스트링 토크나이저를 사용해 입력 받은 값 인접 행렬에 넣기
4. 플로이드-워셜 알고리즘 실행
   a. 반복문 세 개 이용(경유지 k, 출발지 i, 목적지 j)
   b. i->k->j일 때, i에서 j로 바로는 못가지만 k를 거치면 갈 수 있기 때문에 만약 graph[i][k]와 graph[k][j]가 모두 길이 있다면(1이라면) graph[i][j]도 길이 있게 됨
   c. 이 문제의 경우에서는 가중치가 없기 때문에 갈 수 있다면 모두 1 입력
5. 스트링 빌더에 각각의 출력 값을 넣어 한 번에 출력

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class 경로_찾기 {

    public static void main(String[] args) throws IOException{
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));

        //정점 개수
        int N = Integer.parseInt(bf.readLine());
        //인접 행렬 생성 및 초기화
        int[][] graph = new int[N][N];

        //입력 받은 값 인접 행렬에 저장
        for (int i=0; i<N; i++) {
            //스트링 토크나이저로 입력 받기
            //한 줄 씩 입력 받기 때문에 n만큼 생성 필요
            StringTokenizer st = new StringTokenizer(bf.readLine());
            for (int j=0; j<N; j++) {
                graph[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        //경유지
        //경유지부터 반복이 시작되는 이유 : 예를 들어 1번 노드를 경유했을 때
        //출발지에서 경유지를 거쳐 도착지까지의 최단 경로를 구하는 것이기 때문문
        for (int k=0; k<N; k++) {
            //출발지
            for (int i=0; i<N; i++) {
                //도착지
                for (int j=0; j<N; j++) {
                    //만약 출발->경유, 경유->도착에 1이 있다면
                    if (graph[i][k] == 1 && graph[k][j] == 1) {
                        //출발->도착도 길이 있다는 얘기
                        graph[i][j] = 1;
                    }
                }
            }
        }

        //스트링빌더에 넣어 출력
        StringBuilder sb = new StringBuilder();
        for (int i=0; i<N; i++) {
            for (int j=0; j<N; j++) {
                sb.append(graph[i][j]).append(" ");
            }
            sb.append("\n");
        }

        System.out.println(sb);
    }
}