백준 1916 - 최소비용 구하기

문제 파악

시작점에서 도착점으로 가는 최소 비용을 구하는 문제
-> 다익스트라 알고리즘을 활용해 풀 수 있음

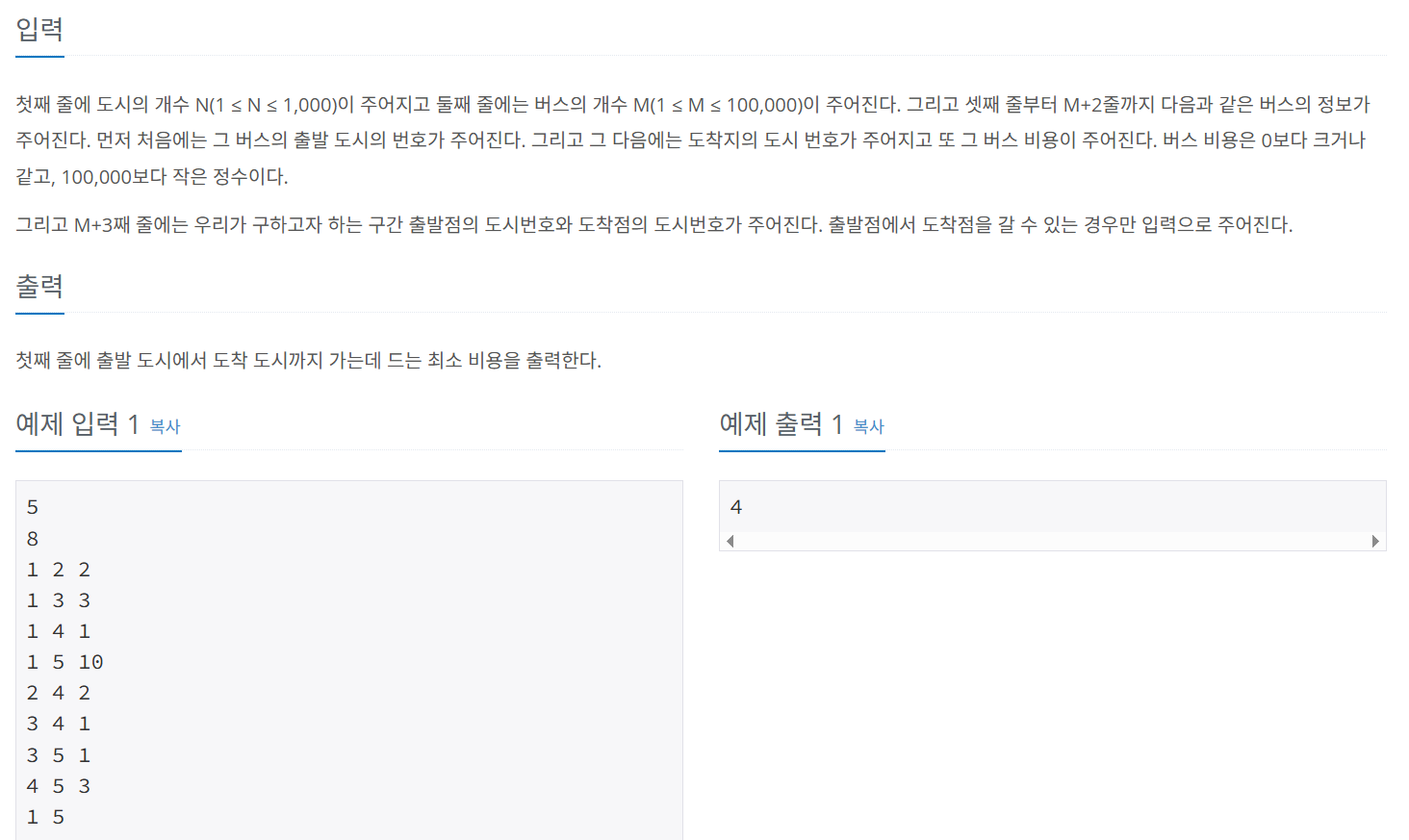
• 입력 :
  N : 도시의 개수 (노드)
  M : 버스의 개수 (간선)
  M개의 각 버스 정보 (출발 도시, 도착 도시, 비용)
  출발 도시 start와 도착 도시 end
• 출력 :
  출발 도시에서 도착 도시로 가는 가장 짧은 비용

가중치가 있고 방향이 있는 그래프
-> 우선순위 큐 사용, 방문 처리 배열로 최소 비용 갱신

풀이

1. 노드 클래스 정의 - comparable 인터페이스 구현
   a. 생성자
   b. 비용 낮은 순부터 정렬 (compareTo 메소드 오버라이딩)
2. 버퍼리더와 스트링 토크나이저를 사용해 입력
   a. 도시 수 n과 버스 수 m 입력받기
   b. 그래프 저장용 인접 리스트 생성
   c. m개의 줄 입력 받아 저장 (출발 도시, 도착 도시, 비용)
3. 출발 도시와 도착 도시 입력 받기
4. 최단 거리 배열 생성 및 초기화
   a. Integer.MAX_VALUE로 배열 초기화
   b. 시작 노드 거리 0으로 설정
5. 다익스트라 알고리즘
   a. 우선순위 큐 생성
   b. 만약 큐에서 꺼낸 도시가 이미 처리된 거리보다 크다면 무시
   c. 아니면 연결된 노드 꺼내면서
   d. 현재 도시까지의 거리 + 다음 도시까지의 비용 계산하면서 갱신
6. 출발 도시에서 도착 도시까지의 최단 거리 출력

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class 최소비용_구하기 {

    static class Node implements Comparable<Node> {
        int city, cost;

        //생성자
        public Node(int city, int cost) {
            this.city = city;
            this.cost = cost;
        }

        //compareTo 메소드 오버라이딩
        public int compareTo(Node other) {
            //오름차순 정렬(비용 작은 것부터)
            return this.cost - other.cost;
        }
    }
    public static void main(String[] args) throws IOException{
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        //도시 개수
        int N = Integer.parseInt(bf.readLine());
        //버스 개수
        int M = Integer.parseInt(bf.readLine());

        //그래프 저장 인접리스트 생성
        List<List<Node>> graph = new ArrayList<>();
        //도시 번호가 1부터 시작해서 0~n까지 n+1개의 리스트
        for (int i=0; i<=N; i++) {
            graph.add(new ArrayList<>()); 
        }

        //출발 도시, 도착 도시, 비용 입력 받아 그래프에 넣기
        for (int i=0; i<M; i++) {
            st = new StringTokenizer(bf.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());
            //출발 도시 추가
            graph.get(start).add(new Node(end, cost));
        }

        st = new StringTokenizer(bf.readLine());
        //마지막 한 줄 입력(출발 도시, 도착 도시)
        int from = Integer.parseInt(st.nextToken());
        int to = Integer.parseInt(st.nextToken());

        //1번부터 N번까지의 최소 비용 저장 배열
        int[] distance = new int[N+1];
        //모두 무한대로 일단 초기화
        Arrays.fill(distance, Integer.MAX_VALUE);
        
        //큐에 시작 노드 넣어주기
        PriorityQueue<Node> pq = new PriorityQueue<>();
        pq.add(new Node(from, 0));
        //시작 노드에서 자기 자신까지의 거리
        distance[from] = 0;

        //큐가 빌 때까지
        while (!pq.isEmpty()) {
            //가장 비용이 작은 도시 꺼내기
            Node current = pq.poll();
            
            //만약 이미 더 짧은 거리로 방문한적이 있다면
            if (distance[current.city] < current.cost) {
                //무시
                continue;
            }

            //현재 도시에서 갈 수 있는 모든 도시 순회
            for (Node next : graph.get(current.city)) {
                //새로운 경로의 총 비용
                int newCost = distance[current.city] + next.cost;

                //만약 새로운 경로가 기존 경로보다 비용이 적다면
                if (newCost < distance[next.city]) {
                    //갱신
                    distance[next.city] = newCost;
                    //큐에 집어넣어 그 도시에서의 경로도 조사
                    pq.add(new Node(next.city, newCost));
                }
            }
        }
        System.out.println(distance[to]);
    }
}