이번 글부터는 빅데이터 분석 기사 실기에 필요한 여러 함수와 기법에 관해 정리해보겠습니다. 우선 이번 글은 1과목을 대상으로 필요한 함수들과 사용 방식에 관해 정리할 예정이며, 계속 업데이트할 예정입니다.
IQR을 이용한 이상치
IQR을 구하기 위한 방법은 두 가지가 있습니다.
.quantile()
Q1 = df[col].quantile(.25)
Q3 = df[col].quantile(.75)
IQR = Q3 - Q1Q1 = np.percentile(df[col], 25)
Q3 = np.percentile(df[col], 75)
IQR = Q3 - Q1아래 boxplot에서 &Q3 + 1.5IQR& 보다 크거나 &Q1 - 1.5IQR& 보다 작으면 이상치로 분류할 수 있습니다.
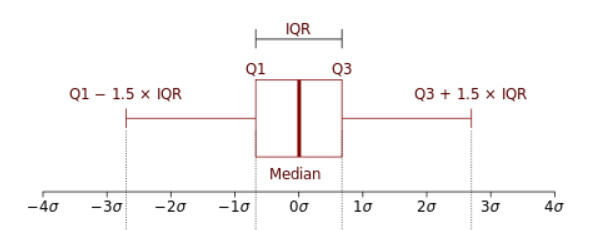
Fare_outlier = df[(df['Fare'] > df['Fare'].quantile(0.75) + 1.5*IQR) | (df['Fare'] < df['Fare'].quantile(0.25) - 1.5*IQR)]소수점 올림, 내림, 버림
내림과 버림은 양수에서는 같지만 음수에서는 -5.5에서 내림을 하면 -6, 버림을 하면 -5가 되는 차이가 있습니다.
.ceil(), .floor(), .trunc()
# 이상치를 포함한 데이터 올림, 내림, 버림의 평균값
up = np.ceil(df['age']).mean()
floor = np.floor(df['age']).mean()
trunc = np.trunc(df['age']).mean().map()
map함수는 '대상':'대상일 때의 값'으로 써주면 됩니다.
# f1결측치 city별 중앙값으로 대체
df['f1'] = df['f1'].fillna(df['city'].map({'서울':s,'경기':k,'부산':b,'대구':d}))왜도, 첨도
왜도와 첨도는 다음과 같이 구할 수 있습니다.
skew(), kurt()
skew = df['SalePrice'].skew()
kurt = df['SalePrice'].kurt()누적합, 표준편차, 절댓값
cumsum(), std(), abs()
df[df['f2']==1]['f1'].cumsum()
enfj_std = enfj['f1'].std()
infp_std = infp['f1'].std()
np.abs(enfj_std - infp_std).std()와 np.abs() 함수로 각각을 구할 수 있습니다.
결측치 처리
fillna(method='bfill'), dropna
# 결측치 처리 (뒤에 나오는 값으로 채움)
df2 = df2.fillna(method = 'bfill')예를 들면, 이러한 것이죠.

결측치를 제거하는 방식은 다음과 같습니다.
df = df.dropna(subset=['r2'])표준화, Min-Max 스케일링
표준화
식을 활용해서 직관적으로 코드를 쓰면
# 표준화
df['f5'] = (df['f5'] - df['f5'].mean()) / (df['f5'].std())sklearn의 StandardScaler를 사용할 수도 있습니다.
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df['f5'] = scaler.fit_transform(df['f5'])Min-Max 스케일링
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
df['f5'] = scaler.fit_transform(df['f5'])을 활용하여 풀 수도 있습니다.
df['f5'] = df['f5'].transform(lambda x: ((x - x.min()) / (x.max() - x.min())))로그 변환, 여존슨/박스콕스 변환
로그 변환
로그 스케일 변환은 두 가지 방법을 사용할 수 있습니다.
np.log(), np.log1p()
## ln(x)
np.log(df['SalePrice'])
## ln(1+x)
np.log1p(df['SalePrice'])np.log1p는 데이터에 0이 포함되어 있을 때 유용합니다.
여존슨/박스콕스 변환
여존슨/박스콕스 변환은 sklearn 패키지를 활용합니다.
power_transform(method='box-cox') 디폴트: 여존슨
from sklearn.preprocessing import power_transform
# 여존슨
power_transform(df[['f1']])
# 박스콕스
power_transform(df[['f1']], method='box-cox')상관관계
.corr()
df_corr = df.corr()상관관계는 절댓값으로 그 크기를 비교합니다.
print(round(abs(df_corr['quality']).max() + abs(df_corr['quality']).min(), 2))시계열 데이터
시계열 데이터 변환
pd.to_datetime()
# datetime으로 type 변경
df['Date'] = pd.to_datetime(df['Date']).dt.year, .dt.weekday, .dt.total_seconds()
df['Year'] = df['Date'].dt.year
df['Month'] = df['Date'].dt.month
df['Day'] = df['Date'].dt.day
df['Dayofweek'] = df['Date'].dt.weekday #0:월요일
df['SessionDuration'] = (df['EndTime'] - df['StartTime']).dt.total_seconds()위의 방식대로 하면 2022년 3주차와 2023년 3주차가 같은 3으로 나와서 문제가 생길 수 있습니다. 따라서 여러 년도가 섞여있는 경우 사용하는 방법을 소개합니다.
parse_dates=[해당열], index_col, resample('W')
df = pd.read_csv(..., parse_dates=['Date'], index_col=0)
# W: 주단위, 2W: 2주 단위, M: 월 단위
df_w = df.resample('W').sum()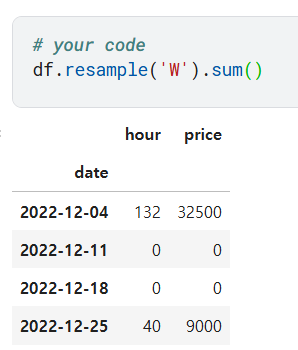
시계열 데이터 출력
print(df['StartDate'].value_counts().index[0].strftime('%Y-%m-%d'))데이터 분할
구간 분할
pd.qcut(분할 대상, q=분할 개수, labels=[분할 후 각 분할의 이름])
구간 분할을 수행해줍니다.
df_sp['range'] = pd.qcut(df_sp['age'], q=3, labels=['group1' , 'group2', 'group3'])특정 행 추출
특정 위치의 데이터가 궁금할 수 있습니다.
.iloc[행]를 사용해 10번째 행의 'f1' 값을 추출합니다.
df.sort_values(by='f1', ascending=False).reset_index().iloc[9]['f1']중복 제거
drop_duplicates(subset=[])
df = df.drop_duplicates(subset=['age'])기간/데이터 쉬프트(shift)
df['previous_PV'] = df['PV'].shift(1)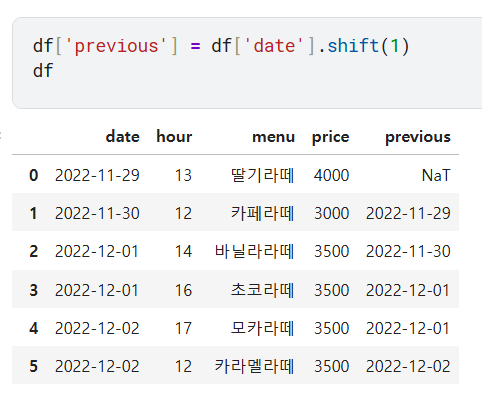
문자열
문자열 슬라이싱
.str()
# 첫 글자가 E인 사람
df['f4'].str[0] == 'E'문자열 포함
.str.contains()
df[df['menu'].str.contains('라떼')]개수 세기
value_counts()
df['date'].value_counts().index[0]melt()
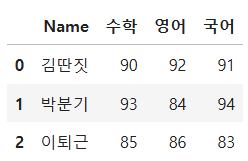
이러한 형식의 데이터프레임을 melt함수를 활용해 변형합니다.
df.melt(id_vars= '기준 열', value_vars= '값을 가져올 열', var_name= '값을 가져올 열 이름', value_name= '값의 이름')
df_melt = df.melt(id_vars='Name', value_vars=['수학', '영어', '국어'],
var_name = '과목', value_name = '점수')
df_melt- id_vars: 기준 열
- value_vars: 값을 가져갈 열
- var_name: value를 가져갈 열의 이름
- value_name: value값들의 열의 이름

df.melt(id_vars='Name', value_vars = ['수학', '영어'], var_name = '과목', value_name= '점수')이렇게 하여 수학과 영어만 부분적으로 추출할 수도 있습니다.
함수 사용법이 잘 생각나지 않는다면,
dir/help을 사용하면 됩니다.print(help(df.melt))
