scipy의 stats 여러 가지 통계 검정 | 빅데이터분석기사 실기 3과목

나나·2025년 6월 11일
statsmodels가설 검정데이터분석통계
0

세 과목 중 가장 익숙하지 않은 영역인 3과목은 통계 검정입니다. 가설 검증을 안해본 것은 아니지만, 주로 하는 영역은 아니라서 남은 기간동안 3과목을 열심히 해보려고 합니다.

t-test

두 집단의 평균 차이가 통계적으로 유의미한지 검증하는 가장 보편적인 통계 방법입니다. 주로 두 집단의 평균을 비교하거나, 하나의 표본이 어떤 기준 값과 유의미하게 다른지 검정하는 데 사용합니다.

데이터의 정규성을 전제로 합니다.

하나의 표본이 어떤 기준 값과 유의미하게 다른지 검정

stats.ttest_1samp(data, mu, alternative=)

상황해석
ttest_1samp(data, mu)평균이 특정 값과 다른지 검정
alternative='greater'평균이 기준보다 큰지 검정
alternative='less'평균이 기준보다 작은지 검정
alternative='two-sided'(디폴트)평균이 기준보다 다른지 (방향 없이) 검정

# H0: 모평균은 75보다 크지 않습니다.
# H1: 모평균은 75보다 큽니다.

from scipy.stats import ttest_1samp

# 데이터
scores = [75, 80, 68, 72, 77, 82, 81, 79, 70, 74, 76, 78, 81, 73, 81, 78, 75, 72, 74, 79, 78, 79]

mu = 75 # 검정할 모평균
alpha = 0.05 # 유의수준

statistic, p_value = ttest_1samp(scores, mu, alternative= 'greater')

print(statistic, p_value)

if p_value < alpha:
	print("귀무가설을 기각합니다. 모평균은 75보다 큽니다.")
else:
	print("귀무가설을 채택합니다. 모평균은 75보다 크지 않습니다.")

독립적인 두 집단의 평균 비교

stats.ttest_ind(group1, group2)

코드설명
ttest_ind(group1, group2)두 그룹의 평균 차이를 검정. ind는 independent (독립)
statistict검정 통계량 (차이의 크기)
p_value유의확률 → 작을수록 "차이가 우연이 아닐 가능성"이 커짐

from scipy import stats

# H0: 약물을 복용한 그룹과 복용하지 않은 그룹의 평균 체온은 유의미한 차이가 없다.
# H1: 약물을 복용한 그룹과 복용하지 않은 그룹의 평균 체온은 유의미한 차이가 있다.

# 데이터 수집
group1 = [36.8, 36.7, 37.1, 36.9, 37.2, 36.8, 36.9, 37.1, 36.7, 37.1]
group2 = [36.5, 36.6, 36.3, 36.6, 36.9, 36.7, 36.7, 36.8, 36.5, 36.7]

# 가설 검정
statistic, p_value = stats.ttest_ind(group1, group2)
print(statistic, p_value)

# 유의성 검정
if (p_value < 0.05):
    print("귀무가설을 기각합니다. 약물을 복용한 그룹과 복용하지 않은 그룹의 평균 체온은 유의미한 차이가 있다.")
else:
    print("귀무가설을 채택합니다. 약물을 복용한 그룹과 복용하지 않은 그룹의 평균 체온은 유의미한 차이가 없다.")

짝지은 데이터: 두 열 간 차이 비교

같은 사람의 전후 변화를 보는 경우, 쌍체표본(짝지은 표본) t-검정을 사용합니다.

stats.ttest_rel(data1, data2, alternative=)

  • 귀무가설(H0): μ\mu >= 0
  • 대립가설(H1): μ\mu < 0
  • μ\mu = (치료 후 혈압 - 치료 전 혈압)의 평균
from scipy import stats

stats.ttest_rel(df['bp_post'], df['bp_pre'], alternative= 'less')

합동 분산 추정량

T-검정에서 등분산을 가정할 때, 두 집단이 따로 놀지 않고 같은 분산을 공유한다고 보기 때문에, 하나의 공통된 분산을 사용해서 T-통계량을 계산합니다.

Sp2=((n1−1)∗S12)+((n2−1)∗S22)n1+n2−2S_p^2 = \frac{((n_1-1) * S_1^2) + ((n_2-1) * S_2^2)}{n_1+n_2-2}

이때 df1df_1은 그룹1의 자유도: n1-1, df2df_2는 그룹2의 자유도: n2-1

t-검정 종류 예시

  • 독립표본 양측검정: 남학생과 여학생의 평균 키가 다른지 검정
  • 독립표본 단측검정: 남학생과 여학생의 키를 비교하여 여학생의 키가 더 낮은지 검정
  • 대응표본 양측검정: 학생들에게 AI 교육 전/후 시험을 보고 성적 변화가 있었는지 확인
  • 대응표본 단측검정: 학생들에게 AI 교육 전/후 시험 성적을 비교하여 성적이 올랐는지 검정

ANOVA

두 개 이상의 집단의 평균에 차이가 있는지 통계적으로 검증하는 방법입니다.

데이터의 정규성을 전제로 합니다.

One-Way ANOVA

3개 이상의 그룹 평균을 비교할 때, 그룹 간 평균이 모두 같은지 하나라도 다른 그룹이 있는지 확인하고자 할 때 사용합니다.

stats.f_oneway(group1, group2, group3, ...)

from scipy import stats

# 데이터
groupA = [85, 92, 78, 88, 83, 90, 76, 84, 92, 87]
groupB = [79, 69, 84, 78, 79, 83, 79, 81, 86, 88]
groupC = [75, 68, 74, 65, 77, 72, 70, 73, 78, 75]

# H0: 그룹 간 평균의 차이가 없다.
# H1: 적어도 하나의 그룹 평균은 다르다.
f_value, p_value = stats.f_oneway(groupA, groupB, groupC)

Two-Way ANOVA (w.ols)

두 개의 범주형 독립 변수가 연속형 변수에 어떠한 영향을 주는지 검정하는 기법입니다.

ols(formula, data=df).fit() -> sm.stats.anova_lm(model)

# 장식의 종류, 지역, 그리고 이 둘의 조합이 판매량에 유의한 영향을 미치는가?: pvalue가 0.05보다 작으면 유의하다고 해석

from statsmodels.api as sm
from statsmodels.formula.api import ols

model = ols('Sales ~ C(Decoration_Type) * C(Region)', data=df).fit()
sm.stats.anova_lm(model)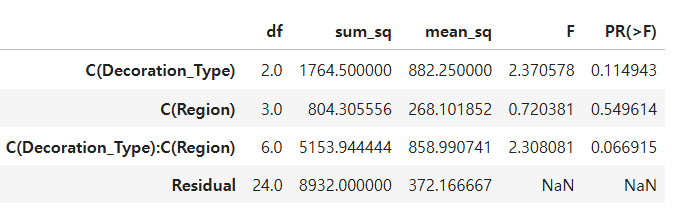

  • 잔차 분석 수행: .resid
residuals = model_full.resid
print("\n7. 잔차의 표준편차:")
print(residuals.std())
  • 신뢰구간 하한: .get_prediction(data).summary_frame(alpha=1-신뢰수준)
# 8. 1번 모델에서 새로운 데이터에 대해 y의 신뢰구간 하한(97% 신뢰수준)을 구하세요.
pred_conf_int_97 = model_full.get_prediction(new_data).summary_frame(alpha=0.03)
conf_lower_97 = pred_conf_int_97['mean_ci_lower'].iloc[0]
print("10. y의 신뢰구간 하한(97% 신뢰수준):", conf_lower_97)

# 9. 1번 모델에서 새로운 데이터에 대해 y의 예측구간 상한(97% 신뢰수준)을 구하세요.
pred_upper_97 = pred_conf_int_97['obs_ci_upper'].iloc[0]
print("11. y의 예측구간 상한(97% 신뢰수준):", pred_upper_97)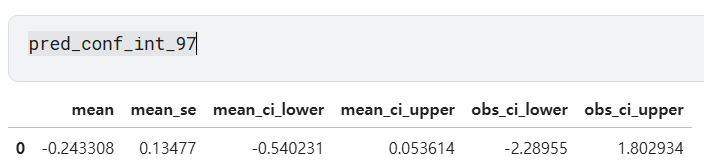

  • mean_ci_lower: 신뢰구간
  • obs_ci_lower: 예측구간

Shaprio-Wilk 검정

정규성을 따르지 않음을 검정하는 방식입니다.
stats.shapiro(data)

from scipy import stats

# H0: 데이터가 정규분포를 따른다.
# H1: 데이터가 정규분포를 따르지 않는다.

data = [75, 83, 81, 92, 68, 77, 78, 80, 85, 95, 79, 89]

statistic, p_value = stats.shapiro(data)

if p_value < 0.05:
	print('귀무가설 기각')
else:
	print('귀무가설 채택, 정규 분포 따름')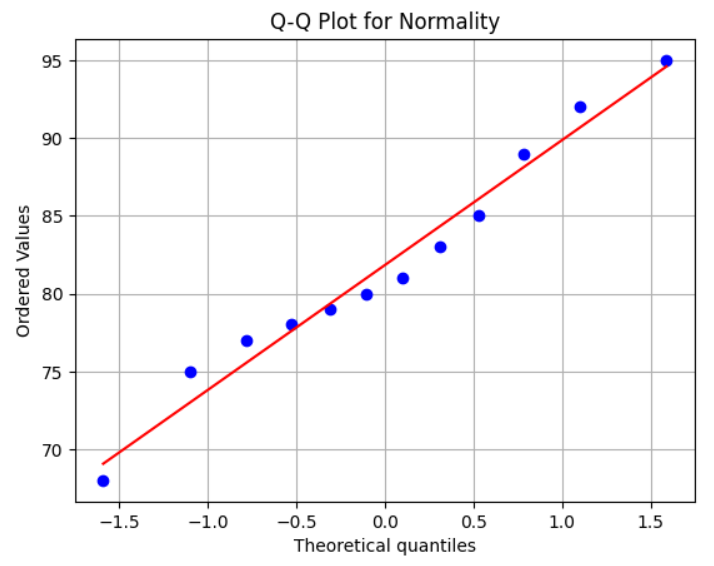


실제로 그림으로 살펴보아도, 정규분포를 따름을 확인할 수 있습니다.


로지스틱 회귀

독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는 데 사용되는 통계 기법입니다.

from statsmodels.formula.api import logit

# Pclass, Gender, SibSp, Parch를 독립 변수로 사용, Pclass는 범주형 변수로 사용
formula = "Survived ~ C(Pclass) + Gender + SibSp + Parch"
model = logit(formula, data=df).fit()
model.params
## model.summary() -> 한 번에 여러 정보를 확인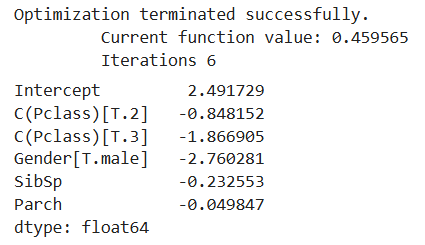

만약, 변수 개수가 너무 많아서 formula를 모두 타이핑하기 어렵다면,

formula = 'Survived ~ ' + '+'.join(df.drop(columns=['Survived']).columns)

.join(컬럼 리스트)함수를 사용하여 한 번에 모델에 적합시킬 수 있습니다.

오즈비, 정확도, 로짓 우도, p-value

  • 오즈비(.params[변수]): income이 1 단위 증가할 때, 구매할 오즈(odds)가 얼마나 변하는지 나타내는 값. 회귀계수는 로그오즈라서, np.exp()로 원래 오즈비 계산
  • 오즈(odds): 어떤 일이 일어날 확률 / 일어나지 않을 확률
from statsmodels.formula.api import logit

formula = 'purchase ~ income'
model_income = logit(formula, data=train)
result_income = model_income.fit()

odds_ratio_income = np.exp(result_income.params['income'])
# result_income.summary()에서 계수 확인 후 np.exp하여 구할 수 있음.
  • 정확도(.predict(데이터))
predictions_income = result_income.predict(test)
predicted_classes_income = (predictions_income > 0.5).astype(int)

accuracy_income = (predicted_classes_income == test['purchase']).mean()
  • 로짓 우도(log-likelihood)(.llf): 값이 클수록 모델이 데이터를 잘 설명한다는 뜻
log_likelihood_income = result_income.llf
# result_income.summary()에서 확인 가능한 정보
  • 잔차이탈도 = -2*(log-likelihood)
-2*result_income.llf
  • p-value(.pvalues[변수])
p_value_income = result_income.pvalues['income']
  • AIC, BIC
    두 수치 모두 작을 때 좋은 모델입니다.
model.aic, model.bic

카이제곱 검정

관찰된 빈도가 기대되는 빈도와 유의미하게 다른지 확인하는 통계적 방법입니다.

stats.chisquare(f_obs= 관측빈도, f_exp= 기대빈도)

from scipy import stats

# H0: 올해 졸업생들의 전공 선택 분포는 과거와 차이가 없다.
# H1: 올해 졸업생들의 전공 선택 분포는 과거와 차이가 있다.

observed_freq = [30, 60, 50, 40, 20]
expected_freq = [200*0.2, 200*0.3, 200*0.25, 200*0.15, 200*0.1]

statistic, p_value = stats.chisquare(f_obs = observed_freq, f_exp = expected_freq)

if p_value < 0.05:
    print("귀무가설 기각, 차이가 있다.")
else:
    print("귀무가설 채택, 차이가 없다.")

카이제곱 독립성 분포

두 범주형 변수 간에 통계적으로 연관이 있는지를 확인하는 검정입니다.

stats.chi2_contingency(data): data는 두 범주형 변수 간의 빈도 -> pd.crosstab으로 구함.

pd.crosstab(df['gender'], df['pass'])
# H0: 성별과 합격 여부는 독립이다.
# H1: 성별과 합격 여부는 독립이 아니다.

from scipy import stats

statistic, pvalue, dof, expected = stats.chi2_contingency(df)
  • expected: 기대빈도 (성별과 합격 여부가 독립일 때의 예상 빈도)

지지도, 신뢰도, 향상도

지표명정의
지지도 (Support) = n(A∩B)전체\frac{n(A \cap B)}{전체}전체 거래 중 A와 B가 동시에 등장한 비율
⇒ P(A∩B)P(A \cap B)
신뢰도 (Confidence) = n(A∩B)n(A)\frac{n(A \cap B)}{n(A)}A가 등장한 거래 중 B도 함께 등장한 비율
⇒ P(B∣A)P(B \mid A)
향상도 (Lift) = conf(A,B)support(B)\frac{conf(A,B)}{support(B)}A가 발생했을 때 B의 발생 확률이 얼마나 높아지는가?
⇒ P(B∣A)P(B)\frac{P(B \mid A)}{P(B)}
⇒ 1보다 크면 양의 연관관계

포아송 분포

포아송 분포는 단위 시간동안 어떤 사건이 몇 번 일어날 확률을 모델링하는데 사용됩니다.
stats.poisson.pmf(몇 번 일어나는지, 단위 시간당 평균 사건 수)
stats.poisson.cmf(몇 번 이하로 일어나는지, 단위 시간당 평균 사건 수)

P(X=k)=e−λ∗λkk!P(X=k) = \frac{e^{-\lambda} * \lambda ^k}{k!}

  • λ\lambda: 단위 시간당 평균 사건 수
  • kk: 사건이 발생하는 횟수
  • pmf(k,λ)pmf(k, \lambda): kk번 일어날 확률
  • cdf(k,λ)cdf(k, \lambda): kk 이하로 일어날 누적 확률
from scipy.stats import poisson

# 평균 발생 횟수
lambda_=3

# 하루에 정확히 5명이 구매할 확률
print(possion.pmf(5, lambda_))

# 하루에 적어도 2명이 구매할 확률 = 1 - 1명 이하 구매할 확률
print(1 - possion.cdf(1, lambda_))

베르누이 분포와 이항분포

stats.binom.pmf(k, n, 베르누이 확률)

from scipy import stats

# 베르누이 분포
## 성공(1), 실패(0)
total = len(df)
success = df['Success'].sum()
success_probability = success / total

# 이항 분포: 100번 중 정확히 60번 성공할 확률
n = 100
k = 60
probability_60 = stats.binom.pmf(k, n, success_probability)

점추정, 구간추정

stats.t.interval(신뢰수준, df= 자유도, loc= 평균, scale= 표준편차/(샘플 수**0.5))

# 점추정: 샘플 평균 계산
sample_mean = temperature_data['Daily Average Temperature'].mean()

# 구간추정: 표준편차 및 신뢰구간 계산
confidence_level = 0.95
sample_std = temperature_data['Daily Average Temperature'].std()
n_samples = len(temperature_data['Daily Average Temperature'])

confidence_interval = stats.t.interval(confidence_level, df=n_samples-1, loc=sample_mean, scale= sample_std/(n_samples**0.5))

F-검정

두 집단 사이의 "분산이 같은지" 확인하는 통계적 방법입니다.

F=S12S22F=\frac{S_1^2}{S_2^2}

F 통계량은 위와 같이 구하고, 일반적으로 F>=1F>=1이 되도록 더 큰 분산을 분산에 둡니다.


정확하게 기억나지 않는 함수나 패키지는 dir이나 help를 적극적으로 활용하면 좋습니다.

print(dir(stats.t))
print(help(stats.t.interval))
profile
나나
데이터에서 의사결정으로
이전 포스트

데이터 분석 기본 모델링 | 빅데이터분석기사 실기 2과목

다음 포스트

유입부터 신청까지, 데이터로 확인하는 참가자 여정: GA4 기반 퍼널 분석

0개의 댓글