[Algorithm] Counting Sort

💡 동작원리

이 글에서는 Counting Sort(계수정렬)에 대해 다뤄보려고 한다. Counting Sort(계수정렬)의 원리는 원소값의 개수를 세고 새로운 배열에 그 갯수에 따라서 위치를 설정해주는 것이다.

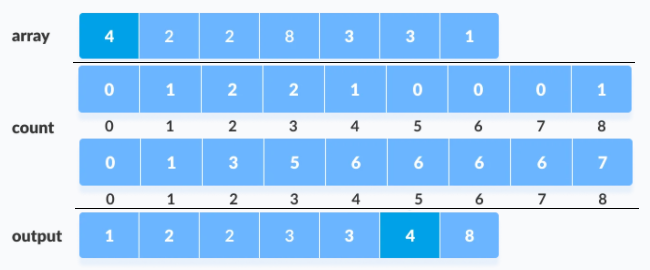
새로운 배열을 선언하고, 정렬할 배열의 원소들을 계산해서 저장해준다. 새로운 배열의 이름을 Count라고 하자. Count의 인덱스 값은 정렬할 배열의 원소값이 될 것이고, Count의 데이터 값은 인덱스 값의 갯수가 될 것이다. 예를들어 정렬할 배열에 3이라는 원소가 5개가 있었다면, Count[3] = 5가 되는 것이다. 정렬할 배열을 i=0부터 i=N-1까지 한 번만 탐색하면 위 그림처럼 Count배열을 채울 수 있다.

이제 Output 배열을 선언하여 기존의 배열을 정렬한다. Output에 올바르게 정렬을 하기 위해서, Count의 값을 Count의 인덱스가 Output에 들어갈 수 있는 최대 인덱스로 바꾸어준다. 이는 Count의 값을 자신보다 앞에 있는 원소들의 합으로 바꾸어주면 된다. Count[i] = Count[i] + Count[i-1] 점화식을 이용한다.

드디어 Output 배열을 채울 수 있게 되었다. 이제는 정렬할 배열을 다시 탐색하며 Count을 참고해 Output 배열에 차곡차곡 원소를 채워넣으면 된다. Output 배열에 원소를 넣을 때마다, Count의 값은 -1을 하여 Output 배열이 완성됐을 때, Count의 값은 Count의 인덱스가 Output에 들어간 최소 인덱스로 되도록 한다. 이것이 Countring Sort(계수정렬)이다.

💻 코드

void Counting_Sort(){
	for (int i = 0; i < N; i++) Count[Arr[i]]++;
	for (int i = 1; i <= Max; i++) Count[i] = Count[i] + Count[i - 1];
	for (int i = 0; i < N; i++){
		Count[Arr[i]]--;
		Output[Count[Arr[i]]] = Arr[i];
	}
}

⏱ 시간복잡도

Countring Sort(계수정렬)의 시간복잡도는 다른 정렬과 다르게 타 원소와 비교를 하여 스왑하는 방식으로 정렬을 하는 것이 아닌, 단지 원소의 개수를 세는 것으로 자연스럽게 정렬이 되는 알고리즘이기 때문에 시간복잡도는 $O(N)$이다.

하지만, 정렬해야하는 데이터 값 중 최대값의 크기만큼의 배열을 선언해줘야하기 때문에 데이터 값의 범위가 넓을 수록 그만큼 공간복잡도가 커져서 실행속도가 늦어진다. 그렇기 때문에 Countring Sort(계수정렬)을 사용하려면 데이터 값의 범위를 반드시 확인해야한다.

$O(N)$