[Algorithm] Quick Sort

💡 동작원리

이 글에서는 Quick Sort(퀵정렬)에 대해 다뤄보려고 한다. Quick Sort(퀵정렬)의 원리는 분할 정복 방법에 있으므로, 분할 파트와, 정복 파트를 나누어서 설명한다.

우선, 분할 파트이다. 정렬해야하는 배열을 Array라고 하자. Array에서의 아무 원소를 골라서 고른 원소를 기준으로 분할을 한다. 이때 고른 원소는 pivot(피벗)이라고 한다. Array에서 pivot보다 작은 값은 pivot의 왼쪽으로, 큰 값은 모두 오른쪽으로 보낸다. 이 과정을 partition(파티션)이라고 한다.

이제 정복 파트를 보자. 정복 파트는 위 분할 파트를 재귀적으로 호출하는 것이다. 앞 과정에서의 pivot의 위치가 q라면, Array의 첫 원소부터 q-1번째 원소까지와 q+1번째 원소부터 마지막 원소까지 다시 분할 파트를 해주는 것이다. 이를 재귀적으로 호출하며 Array를 정렬해 정복한다.

💻 코드

int Partition(int Left, int Right){
	int Pivot_Value = Arr[Left];
	int Left_Mark = Left + 1, Right_Mark = Right;
	while(Left_Mark <= Right_Mark){
		while(Arr[Left_Mark] <= Pivot_Value){ Left_Mark++; }
		while(Arr[Right_Mark] > Pivot_Value){ Right_Mark--; }
		if(Left_Mark < Right_Mark) { swap(Arr[Left_Mark],Arr[Right_Mark]); }
	}
	swap(Arr[Left], Arr[Right_Mark]);
	return Right_Mark;
}
 
void Quick_Sort(int Left, int Right){
	if (Left < Right){
		int Pivot = Partition(Left, Right);
		Quick_Sort(Left, Pivot - 1);
		Quick_Sort(Pivot + 1, Right);
	}
}

위 코드는 Quick Sort(퀵정렬)의 간단한 코드이다.

우선, Partition 함수부분부터 설명하겠다. pivot(피벗)은 항상 정복하려고 하는 부분 배열의 가장 앞을 바라보게 설정했고, Pivot_Value라고 변수명을 설정하여 pivot(피벗)의 데이터값을 저장하였다. pivot(피벗)을 기준으로 작은 값과 큰 값을 나누기 위해서는 두 개의 포인터가 필요해서 Left_Mark, Right_Mark라는 변수를 선언하여 각각 부분 배열의 두 번째 값과 제일 마지막 값을 저장해주었다. 이제 본격적으로 pivot(피벗)을 기준으로 작은 값과 큰 값을 나누어주는데 나누는 방식은 Left_Mark는 오른쪽으로 탐색하며 pivot(피벗)보다 큰 값을 찾고, Right_Mark는 왼쪽으로 탐색하며 pivot(피벗)보다 작은 값을 찾는다. 그 값을 찾게 되면, 서로 스왑해준다. 이를 Left_Mark와 Right_Mark가 만날 때까지 반복해주면 pivot(피벗)을 기준으로 작은 값과 큰 값이 분할이 된다. 마지막으로 pivot(피벗)과 Right_Mark를 스왑해주면 pivot(피벗)보다 작은 값은 앞으로, 큰 값은 뒤로 정렬되게 된다. 그리고 Partition 함수는 pivot(피벗)의 인덱스 값을 리턴해주는데, pivot(피벗)과 Right_Mark를 스왑했기 때문에 Right_Mark를 리턴해주면 된다.

이제 Quick_Sort 함수를 살펴보자. Quick_Sort함수의 제일 첫 부분은 if(Left < Right)인데 이 부분은 배열의 분할을 최소 2개 단위까지 분할 정복하기 위한 것이다. Quick_Sort 함수는 Partition 함수에 비해 비교적 간단하다. Partition 함수로부터 pivot(피벗)의 인덱스 값을 리턴받는다. pivot(피벗)을 기준으로 앞 부분배열과 뒷 부분배열을 나누어서 재귀함수를 호출하여 정복하면 된다. 아래 그림은 코드를 시각적으로 설명한다.

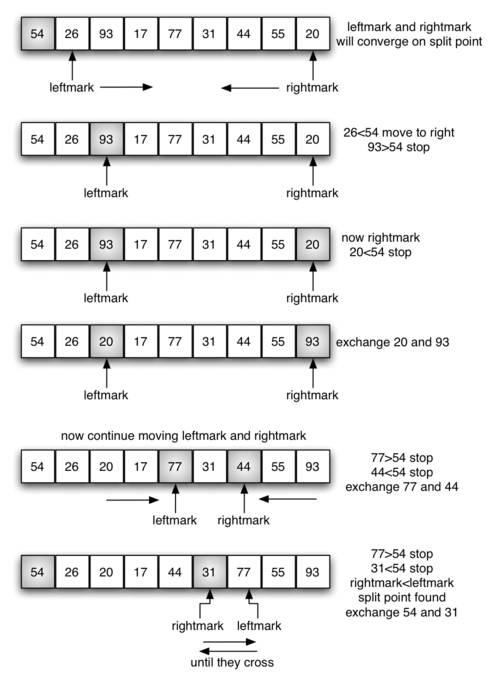
⏱ 시간복잡도

Quick Sort(퀵정렬)은 pivot(피벗)의 인덱스에 따라서 불균등하게 나뉘기 때문에 최선의 경우와 최악의 경우가 나뉘게 된다.

먼저 최선의 경우를 살펴보자. 최선의 경우는 pivot(피벗)이 모든 경우에 정복하려는 배열의 정중앙에 들어가는 것이다. 그렇게 되면 퀵 정렬이 한 번 호출 될 때마다 1/2로 쪼개진다. 따라서, 퀵 정렬의 재귀 호출 깊이는 $log_2N$이다. 한 호출마다 $N$번의 시행이 되기 때문에, 최선의 경우에 시간복잡도는 $O(Nlog_2N)$이다.

이번엔 최악의 경우를 살펴보자. 최악의 경우는 pivot(피벗)이 모든 경우에 정복하려는 배열의 제일 앞에 들어가는 것이다. 그렇게 되면 퀵 정렬의 재귀 호출 깊이는 $N$이 된다. 따라서 최악의 경우에 시간복잡도는 $O(N^2)$이다.

Best case : $O(Nlog_2N)$
Worst case : $O(N^2)$