[Algorithm] Merge Sort

💡 동작원리

이 글에서는 Merge Sort(병합정렬)에 대해 다뤄보려고 한다. Merge Sort의 원리는 배열을 나누었다가, 다시 합치는 것에 있다. 따라서, 분할 정복 알고리즘이라고 할 수 있다. 다시 합치는 과정에서 정렬을 하기 때문에 Merge Sort(병합정렬)이라고 한다.

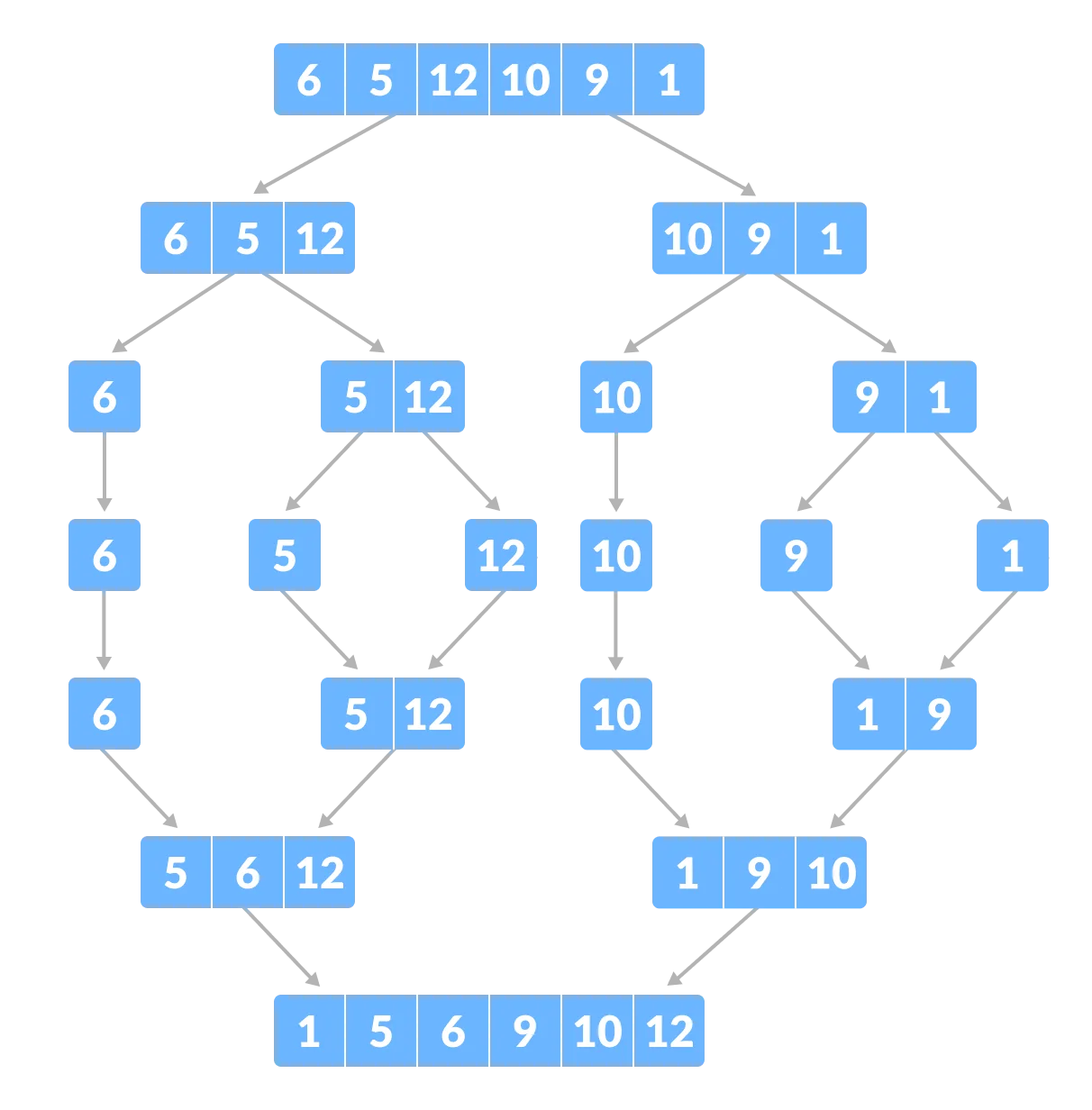
Merge Sort의 첫 단계는 배열을 크기가 1이 될 때까지 분할하는 것이다. 끝이다. 이제 다음 단계로 넘어가자.

Merge Sort의 다음 단계는 분할한 배열들을 정렬하면서 합치는 것이다. 분할된 배열들을 병합할 때는 2개씩 합친다. 분할된 배열 중 왼쪽에 있는 배열(p ~ q)의 인덱스를 가르킬 변수(Left_Index라고 하자), 오른쪽에 있는 배열(q+1 ~ r)의 인덱스를 가르킬 변수(Right_Index라고 하자), 그리고 병합되는 배열의 인덱스를 저장할 변수(Merge_Index라고 하자), 총 세 변수가 필요하다. 또한, 분할된 배열의 데이터들이 정렬된 채로 합쳐질 때, 임시로 저장할 공간이 필요하다. Left_Index에 저장된 값과 Right_Index에 저장된 값을 비교하여 작은 값을 임시 배열의 인덱스가 p인 공간에 저장한다. 그리고 저장된 변수가 다음 원소를 바라볼 수 있도록 +1해준다. 이 방법을 반복하면 두 배열을 병합하는 과정에서 오름차순으로 원소가 저장되게 된다. 만약 Left_Index 또는 Right_Index 중 하나가 분할된 배열의 끝까지 도달하게 되면, 아직 끝까지 도달하지 못한 Index는 남은 원소를 별도의 비교없이 순서대로 저장해주면 된다. 이후 임시 배열에 정렬된 범위(p ~ r)만큼 본래의 배열에 복사해준다.

💻 코드

void Merge(int Left, int Mid, int Right){
	int Left_Index = Left;
	int Right_Index = Mid + 1;
	int Merge_Index = Left;

	while(Left_Index <= Mid && Right_Index <= Right){
		if(Arr[Left_Index] <= Arr[Right_Index]) Sorted[Merge_Index++] = Arr[Left_Index++];
		else Sorted[Merge_Index++] = Arr[Right_Index++];
	}

	if(Left_Index > Mid){ for(int i = Right_Index; i <= Right; i++) Sorted[Merge_Index++] = Arr[i]; }
	else { for(int i = Left_Index; i <= Mid; i++) Sorted[Merge_Index++] = Arr[i]; }

	for(int i = Left; i <= Right; i++){ Arr[i] = Sorted[i]; }
}

void Merge_Sort(int Left, int Right){
	if(Left < Right){
		int Mid = (Left + Right)/2; 
		Merge_Sort(Left, Mid);
		Merge_Sort(Mid + 1, Right);
		Merge(Left, Mid, Right);
	}
}

위 코드는 Merge Sort(병합정렬)의 간단한 코드이다.

먼저 Merge함수에 대해 설명하겠다. 💡동작원리에서 설명했듯이, Left_Index, Right_Index, Merge_Index 세 변수를 선언해주고, 각각 왼쪽 배열의 첫 인덱스, 오른쪽 배열의 첫 인덱스, 병합될 배열의 첫 인덱스를 저장해준다. 그리고 Left_Index, Right_Index 중 하나가 자신의 범위를 넘어갔을 때 멈추는 조건으로 반복문을 만들어준다. 이때 두 Index의 값을 비교하며 오름차순에 맞게 Sorted(임시배열)에 차근차근 원소를 저장해준다. 이후 두 Index 중 아직 다 저장을 못해준 배열을 마저 저장해준다. 그리고 마지막으로 Arr(본배열)에 Sorted(임시배열)을 복사해주면 두 배열이 오름차순으로 정리된 채 저장이 된다.

다음은 Merge_Sort함수이다. 우선 조건문으로 Left < Right을 해서 배열이 1개 단위까지 쪼개졌을 때 Merge함수, 즉 병합이 되도록 해준다. 배열이 1개 단위로 쪼개는 방법은, Mid 변수를 선언하여 Merg_Sort함수를 Left부터 Mid까지, Mid+1부터 Right까지 재귀호출방식을 사용한다. 조건문에 의해 배열이 1개 단위까지 쪼개지게 될 것이고, 이후에 Merge함수가 호출되어 배열 전체가 병합된다.

⏱ 시간복잡도

Merge Sort(병합정렬)의 시간복잡도를 계산해보면 Quick Sort(퀵소트)의 이상적인 경우의 시간복잡도와 같게 된다. Merge Sort은 Quick Sort와 달리 쪼개지는 것이 항상 일정하기 때문에, 모든 경우에 시간복잡도는 같다. 따라서 Merge Sort의 시간복잡도는 $O(NlogN)$이다.

그러나 Merge Sort의 시간복잡도가 항상 $O(NlogN)$인만큼 단점도 있다. 바로 공간복잡도이다. Merge Sort는 병합하는 과정에서 임시로 저장할 배열의 할당이 필요했다. 따라서 정렬해야하는 배열의 크기만큼의 임시배열이 필요하다. Merge Sort에 필요한 공간은 Quick Sort의 두배이다.

$O(NlogN)$