[Algorithm] Heap Sort

💡 동작원리

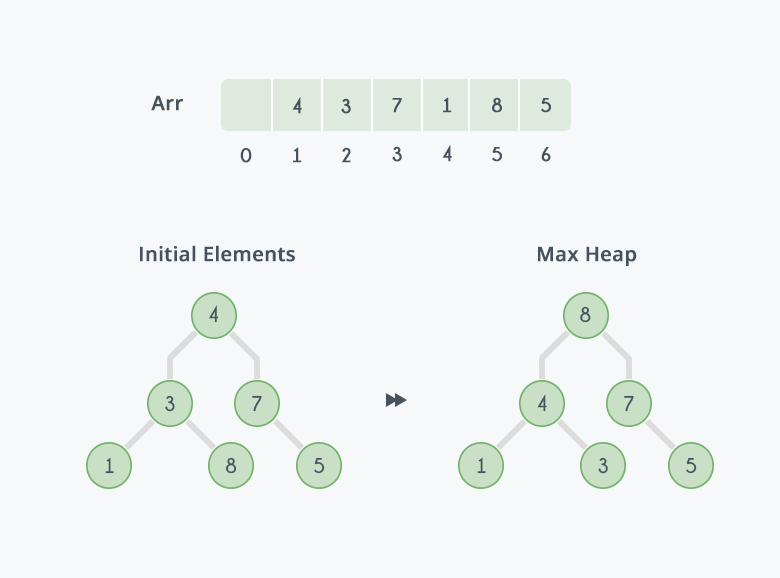
이 글에서는 Heap Sort(힙정렬)에 대해 다뤄보려고 한다. Heap Sort(힙정렬)의 원리는 완전이진트리(complete binary tree)에 있다. complete binary tree(완전이진트리)란, 트리의 모든 Node가 빈 공간 없이 순차적으로 채워져 있는 Tree를 말한다. 오름차순으로 정렬을 할 때는 Max Heap(최대힙), 내림차순으로 정렬을 할 때는 Min Heap(최소힙)을 이용한다. 이때, Max Heap(최대힙)과 Min Heap(최소힙)이란 complete binary tree(완전이진트리)이며, 각각 "부모의 노드값이 자식의 노드값보다 큰 꼴", "부모의 노드값이 자식의 노드값보다 작은 꼴"이다. 본인은 오름차순으로 정렬하는 Heap Sort(힙정렬)을 설명할 것이기 때문에, Max Heap(최대힙)을 사용한다.

Heap Sort(힙정렬)의 첫 번째 단계는 배열을 complete binary tree(완전이진트리)로 바라보고, 이를 Max Heap(최대힙)으로 만드는 것이다. 배열을 complete binary tree(완전이진트리)로 바라보는 방법은 따로 작성하지 않겠다. Max Heap(최대힙)으로 배열이 정리되어 있어야 뒤에 나올 Heapify 함수를 이용하여 배열을 오름차순으로 정렬할 수 있기 때문이다. Heapify 함수는 Tree내에서의 어떠한 원소가 Max Heap(최대힙)의 성질에 맞게 자기 자리를 찾아가는 과정이다. complete binary tree(완전이진트리)를 Max Heap(최대힙)으로 바꾸는 과정에서 Heapify 함수를 사용한다. 바꿔주는 과정은 원소가 배열의 1부터 N까지 있을 때, N/2번째 원소부터 1까지 Heapify 함수를 실행시켜주는 것이다. N/2번째 원소부터 실행시켜주는 이유는 complete binary tree(완전이진트리)의 특성상 N/2+1번째 원소부터는 자식노드가 없기 때문이다.

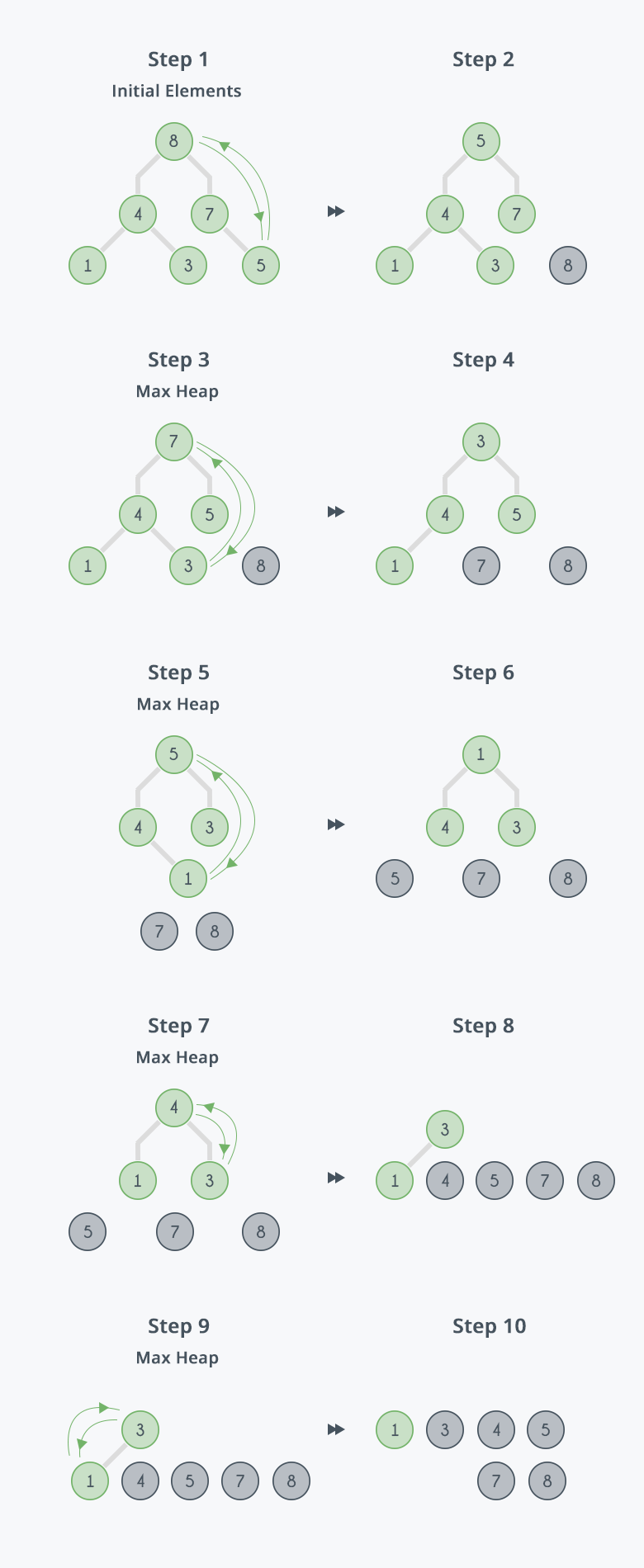
Heap Sort(힙정렬)의 두 번째 단계는 Max Heap(최대힙)의 성질과 Heapify 함수를 이용하여 배열을 오름차순으로 정렬하는 것이다. Max Heap(최대힙)의 성질에 의해서 Root Node가 모든 Node 중 가장 큰 Node일 것이다. 우리는 오름차순으로 배열을 정렬하고 있기 때문에, 이 Root Node와 N번째 원소를 스왑해준다. 그럼 배열 중 가장 큰 값이 제일 뒤로가고, Max Heap(최대힙) 상태가 깨지게 된다. 하지만 이전에 Max Heap(최대힙)상태에서 단 한 원소만 바뀐 것이기 때문에, Heapify함수를 이용해서 바뀐 Root Node를 올바른 위치로 보내주기만 하면 Max Heap(최대힙) 상태가 곧바로 돌아오게 된다. 따라서 Heapify함수를 이용해 Root Node를 올바른 위치로 보내주는데, 이때 유의해야할 점은 배열의 제일 끝에 저장된 가장 큰 값을 제외하고 1부터 N-1까지만 Heapify함수를 실행시켜야한다. 그럼 1부터 N-1까지 Max Heap(최대힙)상태가 되는데, 이때 다시 Root Node와 N-1번째 원소를 스왑해준다. 이후 다시 Heapify함수를 이용해 1부터 N-2까지 Max Heap(최대힙)을 만들어준다. 이를 계속 반복하면 배열이 오름차순으로 정렬된다.

💻 코드

void Heapify(int Cur, int N){
	int Cur_Idx = Cur;
	int Left_Child = Cur*2;
	int Right_Child = Cur*2 + 1;

	if ((Left_Child <= N) && (Arr[Left_Child] > Arr[Cur_Idx])) Cur_Idx = Left_Child;
	if ((Right_Child <= N) && (Arr[Right_Child] > Arr[Cur_Idx])) Cur_Idx = Right_Child;
     
	if (Cur_Idx != Cur){
		swap(Arr[Cur_Idx], Arr[Cur]);
		Heapify(Cur_Idx, N);
	}
}

void Heap_Sort(){
	for(int i = N/2; i >= 1; i--){ Heapify(i, N); }
	for (int i = N; i >= 2; i--){
		swap(Arr[i], Arr[1]);
		Heapify(1, i - 1);
	}
}

위 코드는 Heap Sort(힙정렬)의 간단한 코드이다.

우선 Heapify 함수에 대해 설명하겠다. Cur은 제자리를 찾아가야하는 원소의 위치이고, Cur_Idx에 다시 저장한다. Left_Child와 Right_Child는 배열을 complete binary tree(완전이진트리)의 성질을 이용하여 각각 저장해준다. 제자리를 찾아가야하는 원소 중 자신보다 더 큰 자식이 있다면 바꿔줘야한다. 이때 두 자식이 모두 자신보다 크면 두 자식 중 더 큰 자식을 저장해주어야한다. 이를 감안하여 코드가 짜여 있는데, Left_Child가 더 커서 Cur_Idx에 저장이 되었더라도, 다시 Right_Child가 더 크면 Cur_Idx에 Right_Child가 저장되게 코드가 짜여있다. 이후 Cur_Idx가 변화를 했다면, 기존의 Cur과 스왑을 하여 원소과 그 자식을 스왑해주고 Heapify함수를 재귀호출해준다.

다음은 Heap_Sort 함수이다. 첫 번째 줄의 반복문은 정렬이 되지 않은 배열을 Max Heap(최대힙)으로 바꿔주기 위한 것이다. 코드에 대한 설명은 위에서 했기 때문에 하지 않겠다. 자, 이제 배열은 Max Heap(최대힙)으로 정렬이 되었다. 이제 Max Heap의 Root Node를 제일 뒤로 보내주고 다시 Heapify함수를 호출하여 Max Heap(최대힙)을 만들고, 이를 Max Heap(최대힙)의 크기가 2가 될 때까지 반복해준다. 그럼 배열은 오름차순으로 정렬된다.

⏱ 시간복잡도

Heap Sort(힙정렬)의 시간복잡도를 계산해보자. 먼저 Heapify 함수의 시간복잡도를 계산해야한다. Heapify 함수의 시간복잡도는 최대 $logN$이다. complete binary tree(완전이진트리)의 성질에 의해 깊이가 $logN$이 되고, 최대깊이까지 재귀호출이 되었을 때 최대 시간복잡도가 나오기 때문이다.

이제 Heap Sort(힙정렬)의 시간복잡도를 계산해보자. Heap_Sort() 함수에서 Max Heap을 생성해줄 때 걸리는 시간복잡도는 Heapify함수를 N/2만큼 실행하기 때문에, $O(NlogN/2) = O(NlogN)$이 된다. 또한, 오름차순으로 정렬하는 반복문에서도 Heapify함수가 $N-1$번 실행이 되기 때문에 시간복잡도가 $O((N-1)logN) = O(NlogN)$이 된다. 따라서, Heap Sort(힙정렬)의 시간복잡도는 $O(NlogN)$이다.

$O(NlogN)$