[TIL] 내배캠 사전캠프 7일차

Big O란?

Big O 표기법은 퍼지(fuzzy) 계산을 공식적인 표현.
정식으로 입력된 내용이 늘어날 수록 알고리즘에 실행 시간이 어떻게 변하는지 설명하는 공식적인 방식이다.

Big O는 어떤 함수의 입력 값이 늘어나는 것과 함수 실행 시간이 변하는 관계를 의미한다. 즉, 입력의 크기와 실행시간의 관계를 말한다.

다른 내용에는 상관 하지 않고, 오로지 전반적인 추세(trends)에 주목 하는것이다.

---

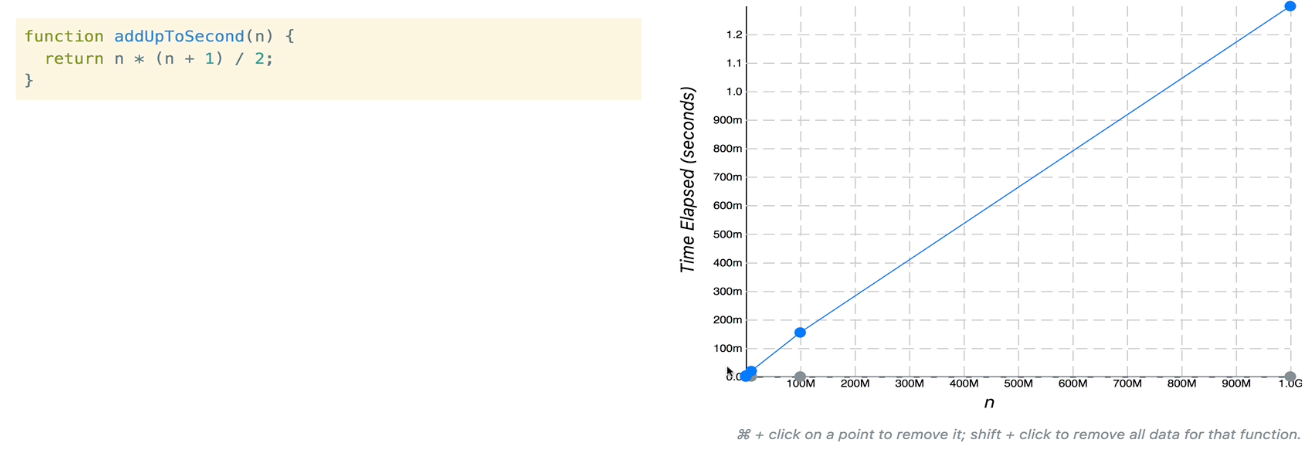
첫번째 함수에서 N의 값이 늘어났지만, 실행 되는 시간에는 아무 영향을 받지 않는다.

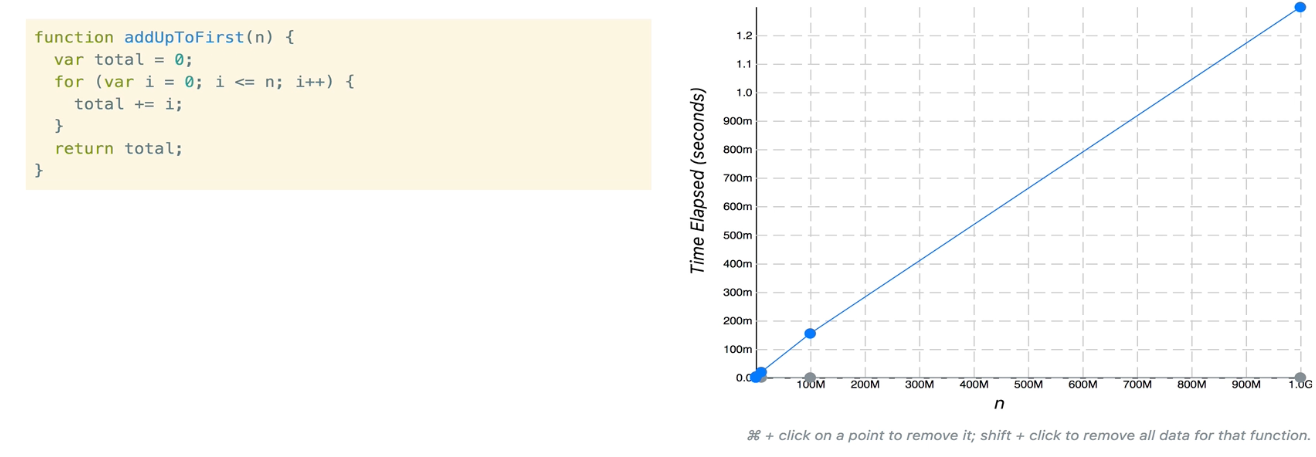
두번째 함수는 실행 되는 시간이 N의 값이 늘어나는 것과 비례하게 거의 1:1 비율로 선형이 늘어났다는걸 볼 수 있다.

이게 바로 Big O이다.

---

컴퓨터가 수행해야 하는 단순 연산 횟수가 n이 증가함에 따라 결국 상수 곱하기 f(n)보다 작아지면 알고리즘이 O(f(n))라고 한다.. (?)

function addUpTo(n) {
  return n * (n + 1) / 2;
}

위의 함수는 O(1)

function addUpTo(n) {
  let total = 0;
  for (let i = 0; i <= n; i++) {
    total += i;
  }
  return total;
}

위의 함수는 O(n)

function countUpAndDown(n) {
  console.log('Going up!');
  for (let i = 0; i < n; i++) {
    console.log(i);
  }
  console.log('At the top! \n Going down...');
  for (let j = n - 1; j >= 0; j--) {
    console.log(j);
  }
  console.log('Back down. bye!');
}

위의 함수에서 Big O를 찾는다면 첫번째 for문으로 O(n) 두번째 for문으로 O(n)이므로 정확히는 O(2n)이지만 Big O는 추세를 보기 때문에 위의 함수의 Big O는 O(n)이다.

O(n) 함수의 일반적인 그래프 모습이다.

function printAllPairs(n) {
  for (let i = 0; i < n; i++) { 
    for (let j = 0; j < n; j++) {
      console.log(i, j);
    }
  }
}

위의 함수는 이전 함수들과는 조금 다르다. 중첩 루프가 있는 함수이다.
루프는 n에 기반으로 실행이 되기에 상위 for는 O(n)이 되고 하위 for는 단순히 O(n)이 아니라 중첩 되어 있기 때문에 O(n2)이 된다. 즉, O(n)연산 내부에 O(n)연산이 추가가 되면 O(n2)이 된다.

이런 경우는 n이 커질수록 실행 시간이 n2의 값으로 늘어난다는 것이다.

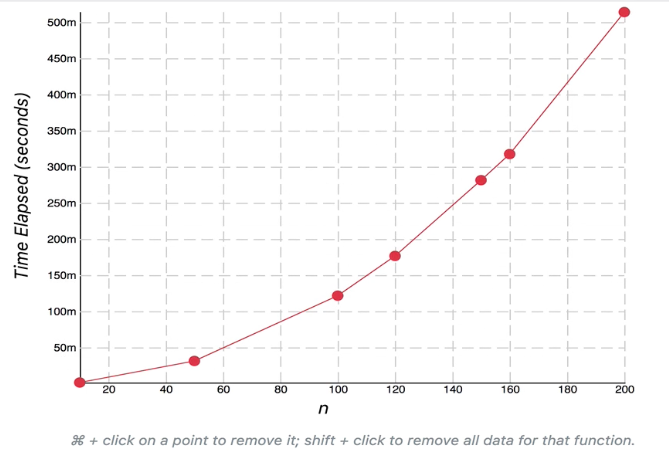
이 전의 그래프들과는 추세가 다르다. n값과 시간이 비례해서 늘어나는 선형과 다르게 지수 곡선을 그리고 있다는걸 볼 수 있다.

기본적으로 입력인 n이 커질수록 알고리즘이 얼마나 효율적인지 표현하는 방식이라는 것만 기억하자.