출처 링크

---

DDPM

2개의 과정 (Forward process, Reverse process)으로 구성된다.

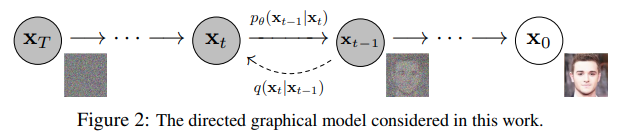
1. a fixed forward diffusion process $\bold{q}$
   점진적으로 gaussian noise를 image에 추가한다.
   pure noise를 얻을 때 까지!
   
2. a learned reverse denoising diffusion process $\bold{p_{\theta}}$
   신경망이 pure noise로부터 image를 denoise한다.
   actual image를 얻을 때 까지!

---

결국, 신경망이 최적화할 수 있는, 계산 가능한 loss function이 필요하다.

Forward Process

Noise를 추가해서 pure Gaussian noise 만들기

1) Original Forward process

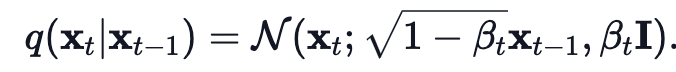
각 time step $\bold{t}$에서의 새로운 image는
conditional gaussian distribution에서 뽑는다.
$\mu_t=\sqrt{1-\beta_t}\bold{x_{t-1}}$, $\sigma_t^2=\beta_t$
$\\$
$\epsilon \sim N(0,I)$를 샘플링하고, $\bold{x_t}$를 아래와 같이 세팅한다.
$\bold{x_t}=\sqrt{1-\beta_t}\bold{x_{t-1}} + \sqrt{\beta_t}\epsilon$

2) Direct Forward process

• $\bold{x_t}$를 sampling하기 위해서, 여러번 반복적으로 $\bold{q}$를 적용할 필요 없이,
  아래의 수식으로 $\bold{x_0}$로부터 추가된 임의의 noise level에서의 $\bold{x_t}$를 sampling할 수 있는 수식이 발표되었다.
  
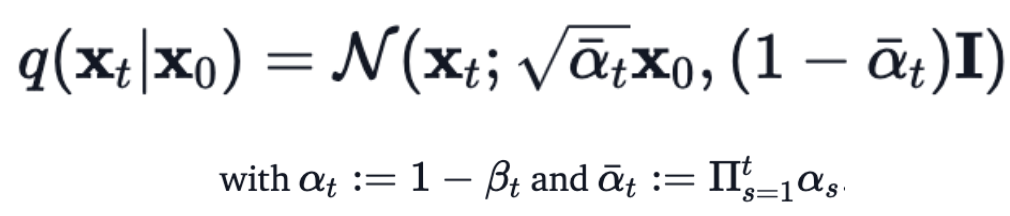
  이 수식을 이용해서
  1) 우리는 이제 Gaussian noise와 scale을 적절하게 $\bold{x_0}$에 추가해서, $x_t$를 바로 sampling할 수 있다.
  2) $\bar{\alpha}_t$는 이미 알려져 있는 $\beta_{t}$ variance schedule로 구성되어 있어서, precomputed될 수 있다.
  3) 뒤에서 논의되지만, 위의 사실은 모델이 training할 때, random한 loss function term을 optimize할 수 있게 해준다.
  (training 때 $t$를 random하게 samping하고, $\bold{L_t}$를 optimize 할 수 있다.)

---

Reverse Process

$\bold{p(x_{t-1}|x_t)}$를 알면 원래 확률 분포 $\bold{x_0}$를 알 수 있지만, 알 수 없으므로, $\\$conditional probability distribution $\bold{p_\theta(x_{t-1}|x_t)}$를 예측하고 학습한다.

$\bold{p(x_{t-1}|x_t}) \approx \bold{p_{\theta}(x_{t-1}|x_t)} = N({\bold{x_{t-1};\mu_{\theta}(x_t, t), \sigma_t^2I}})$

• 만약, 우리가 conditional distribution $\bold{p(x_{t-1}|x_t})$를 알고 있다면,
  우리는 reverse process를 바로 진행할 수 있다.
  random한 Gaussian noise $\bold{x_T}$를 샘플링해서, 점차 denoise하면, real distribution $\bold{x_0}$를 얻게 되기 때문이다.

• 하지만, 우리는 $\bold{p(x_{t-1}|x_t})$를 알지 못한다.
  $\bold{p(x_{t-1}|x_t})$를 계산하기 위해선, conditional probability 계산을 위해 모든 가능한 images의 distribution을 알아야 하기 때문이다.
  그렇기 때문에, 우리는 신경망이 $\bold{p_{\theta}(x_{t-1}|x_t)}$라는 conditional probability distribution을 추정하는(학습하는) 방법을 이용한다.
  $\theta$는 신경망의 parameters로, gradient descent로 업데이트 되는 값이다.
  

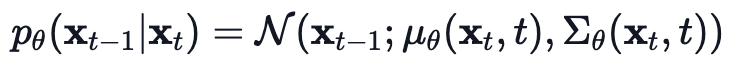
• 우리의 신경망은 평균과 분산을 학습해야 한다.
  하지만, DDPM에서는 분산은 고정시키고(fixed),
  신경망이 오직 conditional probability distribtuion $\bold{p_{\theta}(x_{t-1}|x_t)}$의 평균$(\mu_{\theta})$만 학습하도록 했다.

---

Loss Function

신경망이 예측한 확률 분포 $\bold{p_{\theta}}$ 의 평균($\mu$)과 확률 분포 $\bold{q}$의 평균($\tilde{\mu}$)의 차이를 줄여서
$\bold{p_{\theta}}$를 $\bold{q}$와 유사하게 만드려는 Loss 함수는,
< reparameterization을 통해서>
신경망이 예측한 noise $\bold{\epsilon_{\theta}}$와 실제 noise $\bold{\epsilon}$ 간의 차이를 줄이는 방식으로 바뀐다.
결론적으로는 "mean predictor"가 아닌, "noise predictor" 신경망을 만드는 것이다.

• reverse process에서 mean을 학습하는 Loss 함수를 정의하기 위해서, 저자는 $\bold{q}$와 $\bold{p_{\theta}}$의 조합을 VAE와 같이 생각할 수 있음을 관찰했다.
  그러므로, variational lower bound (=ELBO)는 GT data sample $\bold{x_0}$에 대해서 negative log-likelihodd를 최소화하는데 사용될 수 있다.

• ELBO는 각 time step $\bold{t}$의 loss들의 합으로 정의될 수 있음이 밝혀졌다.
  $\bold{L=L_0+L_1+...+L_T}$
  forward $\bold{q}$ process와 backward process의 구조에 의해서, $L_0$를 제외한 각 loss term은 각 $\bold{q}$와 $\bold{p_{\theta}}$의 Gaussian distribution 사이의 KL-Divergence이다.
  그리고 이 KL-Divergence는 평균 간의 L2-loss로 표현될 수 있다.

• Loss들을 구성하는 KL-Divergence term 안의 noise level $\bold{t}$에 대해서,
  신경망이 $\bold{\epsilon_{\theta}(x_t, t)}$ 네트워크를 통해 더해진 noise를 학습(예측)할 수 있도록 평균(mean)을 reparametrization할 수 있다.
  이는 우리의 신경망이 mean predictor 대신, noise predictor가 됨을 의미한다.
  $\\$
  평균(mean)은 아래와 같이 계산된다.
  
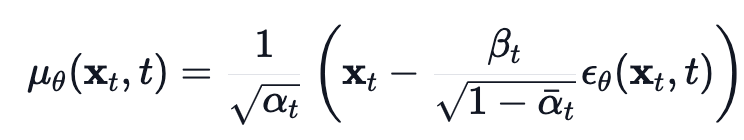
  그리고 최종적인 Loss function $L_t$는 아래와 같이 계산된다.
  ($\epsilon \sim N(0,I)$이 주어졌을 때, random time step $t$에 대해서)
  
  $\\$
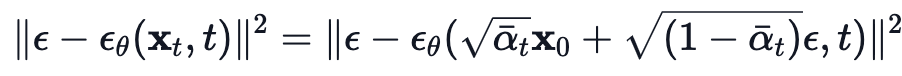
  여기서, $\bold{x_0}$는 initial real image이고 (실제 data distribution, 다시 말해 "real images"에서 sampling한),
  $\bold{t}$는 fixed forward process에서 sampling한 direct noise level이다.
  $\epsilon$은 time step $t$에서 sampling한 pure noise이고,
  $\bold{\epsilon_{\theta}(x_t,t)}$는 우리의 신경망이다.
  $\\$
  신경망은 간단한 MSE(mean squared error)를 사용해 true Gaussian noise와 predicted gaussian noise 간의 loss를 줄이며 최적화된다.
  

신경망 Training 방법 정리

한 번 더 간단하게 정리하자면,
1) real unknown and possibly complex data distribution $\bold{q(x_0)}$로부터
random sample $\bold{x_0}$를 뽑는다.
2) $\bold{1}$과 $\bold{T}$ 사이의 noise level (= random time step) $\bold{t}$를 뽑는다.
3) Gaussian distribution으로부터 noise를 뽑는다.
4) input $\bold{x_0}$를 noise level $\bold{t}$만큼 노이즈를 추가한다.
(known scheldue $\beta_t$ 만큼 noise가 추가된다.)
5) 신경망은 노이징된 image $\bold{x_t}$에 추가된 noise를 예측하도록 training한다.

• 실제 구현에선, 데이터의 여러 batch들에서 위 과정이 이루어진다. 그리고 stochastic gradient descent를 사용해 신경망을 최적화한다.